[转]趣题：一个n位数平均有多少个单调区间？---- From Matrix67

考虑这么一个 14 位数 02565413989732 ，如图所示，它的数字先逐渐变大，然后开始变小，再变大，再变小，再变大，再变小。我们就说，它一共包含了 6 个单调区间。我们的问题就是：一个 n 位数平均有多少个单调区间？为了避免歧义，我们假设任意两位相邻的数字都不相同，因而像 77765589911 这样的数我们就不考虑了。另外，大家可能已经注意到了，我们允许这个 n 位数以数字 0 开头。因而，更精确地说，我们的问题是：相邻数字都不相同的、允许以 0 开头的所有 n 位数当中，平均有多少个单调区间？

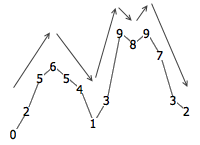
这个题目来自 1987 年 IMO 候选题。

让我们把所有这种 n 位数的个数记作 N 。那么 N 等于多少？这个 n 位数的第一位有 10 种选择，今后的每一位都只有 9 种选择（因为要跟前一位不一样），因而 n 位数一共有 N = 10 · 9n-1 个。接下来，我们要求的就是，所有 n 位数当中的所有单调区间一共有多少个。我们换一种方法来累计这些单调区间：先算所有从第一位开始的单调区间，再算所有从第二位开始的单调区间，等等，最后算所有从第 n 位开始的单调区间。如果用 ri 来表示所有从第 i 位开始的单调区间的数目，那么我们要求的平均单调区间数就是 (r1 + r2 + … + rn) / N ，也就是 r1 / N + r2 / N + … + rn / N 。注意到其中的每一项 ri / N 其实就是从 N 个合法的 n 位数中任取一个后，存在以第 i 位数打头的单调区间的概率。因此，我们只需要求出这 n 个概率值，加起来便是我们想要的答案了。

显然， r1 / N = 1 ，因为第一位数字必然会引领一个单调区间。显然， rn / N = 0 ，因为最后一位数字不可能引领一个新的单调区间。那么，对于其他的 ri / N 呢？注意到，第 i – 1 位、第 i 位和第 i + 1 位的大小关系一共可能有以下四种情况：

其中，只有第三种情况和第四种情况下，第 i 位才会成为一个新的单调区间的开始。为了计算这两种情况发生的概率，我们只需要算出情况 1 和情况 2 发生的概率，再用 1 来减即可。情况 1 发生的概率有多大呢？三位数字串一共有 10 · 92 个（第一位有 10 种选择，后面的每一位都只有 9 种选择，因为要跟前一位不一样）。为了得到递增的数字串，我们只需要选出三个不同的数字，然后把它们从小到大排列即可，这一共有 C(10, 3) 种方法。因此，情况 1 的发生概率就是 C(10, 3) / (10 · 92) = 4/27 。同理，情况 2 的发生概率也是 4/27 ，两者加起来就是 8/27 ；反过来，情况 3 和情况 4 出现的概率就是 1 – 8/27 = 19/27 了。

因此，我们最终要求的答案就是 1 + 19/27 + 19/27 + … + 19/27 + 0 = 1 + (n – 2) · 19/27 。

这个结论还会引出很多有意思的问题。在一个 29 位数当中，平均会产生 20 个单调区间。我们似乎发现了一个很不合理的地方：这岂不意味着，平均每个单调区间的长度只有 29/20 = 1.45 个数字吗？考虑到单调区间的长度不可能恰好是 1.45 个数字，为了得到 1.45 这个平均长度，一定有些区间的长度比 1.45 小，有些区间的长度比 1.45 大。有些区间的长度比 1.45 小，这不就意味着这些区间的长度为 1 吗？而一个区间的长度显然是不可能为 1 的。怎么回事？

其实， 29/20 = 1.45 这个算式是错的。在这 20 个单调区间中，除了最后一个区间以外，每一个区间的最后一个数与下一个区间的第一个数都是公共的。因此，这个 29 位数当中，有 19 个数被重复使用了。所以，在一个 29 位数当中，单调区间的平均长度应该是 (29 + 19) / 20 = 2.4 。

类似的， n 位数的单调区间的平均长度为 (n + (19/27)(n – 2)) / (1 + (19/27)(n – 2)) = (46n – 38) / (19n – 11) = (46 – 38/n) / (19 – 11/n) 。当 n 无穷大时，其极限为 46/19 。

参考资料：Ross Honsberger, From Erdos to Kiev: Problems of Olympiad Caliber, pp. 29-33