POJ 题目1145/UVA题目112 Tree Summing（二叉树遍历）

Tree Summing

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 8132		Accepted: 1949

Description

LISP was one of the earliest high-level programming languages and, with FORTRAN, is one of the oldest languages currently being used. Lists, which are the fundamental data structures in LISP, can easily be adapted to represent
other important data structures such as trees.



This problem deals with determining whether binary trees represented as LISP S-expressions possess a certain property.


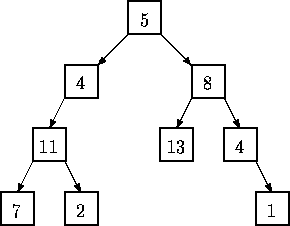
Given a binary tree of integers, you are to write a program that determines whether there exists a root-to-leaf path whose nodes sum to a specified integer. For example, in the tree shown below there are exactly four root-to-leaf paths. The sums of the paths
are 27, 22, 26, and 18.




Binary trees are represented in the input file as LISP S-expressions having the following form.

empty tree ::= ()

tree 	   ::= empty tree (integer tree tree)

The tree diagrammed above is represented by the expression (5 (4 (11 (7 () ()) (2 () ()) ) ()) (8 (13 () ()) (4 () (1 () ()) ) ) )




Note that with this formulation all leaves of a tree are of the form (integer () () )




Since an empty tree has no root-to-leaf paths, any query as to whether a path exists whose sum is a specified integer in an empty tree must be answered negatively.

Input

The input consists of a sequence of test cases in the form of integer/tree pairs. Each test case consists of an integer followed by one or more spaces followed by a binary tree formatted as an S-expression as described above. All
binary tree S-expressions will be valid, but expressions may be spread over several lines and may contain spaces. There will be one or more test cases in an input file, and input is terminated by end-of-file.

Output

There should be one line of output for each test case (integer/tree pair) in the input file. For each pair I,T (I represents the integer, T represents the tree) the output is the string yes if there is a root-to-leaf path in T
whose sum is I and no if there is no path in T whose sum is I.

Sample Input

22 (5(4(11(7()())(2()()))()) (8(13()())(4()(1()()))))
20 (5(4(11(7()())(2()()))()) (8(13()())(4()(1()()))))
10 (3
     (2 (4 () () )
        (8 () () ) )
     (1 (6 () () )
        (4 () () ) ) )
5 ()

Sample Output

yes
no
yes
no

Source

Duke Internet Programming Contest 1992,UVA 112

题目大意：给出一个二叉树的表达式，问有没有一个路径和是n

ac代码

Problem: 1145		User: kxh1995
Memory: 164K		Time: 0MS
Language: C++		Result: Accepted

#include<stdio.h>
int tree_sum(int n)
{
	int ans=0,m;
	if(scanf(" (%d",&m))
	{
		ans=tree_sum(n-m)+tree_sum(n-m);
		if(ans<2)
			ans=0;
	}
	else
		ans=!n;
	scanf(" )");
	return ans;
}
int main()
{
	int n;
	while(scanf("%d",&n)!=EOF)
	{
		if(tree_sum(n))
			printf("yes\n");
		else
			printf("no\n");
	}
}