斐波那契数列第N项f(N)[矩阵快速幂]

矩阵快速幂

　　定义矩阵A（m*n），B（p*q），A*B有意义当且仅当n=p。即A的列数等于B的行数。

　　且C=A*B，C（m*q）。

　　例如：

　　进入正题，由于现在全国卷高考不考矩阵，也没多大了解。因为遇到了斐波那契这题...

　　注意到： F_n+1=F_n+F_n-1

　　我们会有：

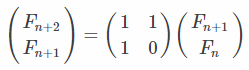
　　则：

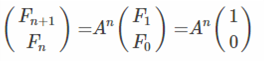
　　所以我们只需要想办法求矩阵A的幂，这时候我们当然想要用快速幂。

---

代码部分：

定义矩阵：

struct matrix{
    ll a[][];
};

（类比整数的快速幂）预处理：

[我们需要一类似于1的矩阵：]

『1 0 0

0 1 0

0 0 1』类似这种操作...

void init(){
        int i,j;
        memset(res.a,,sizeof res.a);
        ;i<=;i++) res.a[i][i]=;
        ][]=;
        ][]=;
        ][]=;
        ][]=;}

矩阵乘法：[就该题而言]

matrix mul(matrix p,matrix q){
        int i,j,k;
        matrix m;
        memset(m.a,,sizeof m.a);
        ;i<=;i++)
            ;j<=;j++)
                ;k<=;k++)
                    m.a[i][j]=(m.a[i][j]+p.a[i][k]*q.a[k][j])%Mod;
        return m;
}

快速幂：

void mfpow(ll p){
        init();
        while(p){
            ) res=mul(base,res);
            base=mul(base,base);
            p>>=;
        }
 }

全部的代码：（lowbee的难免会差一些，请大佬们见谅...）

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 typedef long long ll ;
 inline ll read();
  ;
 struct matrix{
     ll a[][];
 };
 matrix res,base;
 ll ans;
 ll c[];
 ll n;
 namespace lys{
     void init(){
         int i,j;
         memset(res.a,,sizeof res.a);
         ;i<=;i++) res.a[i][i]=;
         ][]=;
         ][]=;
         ][]=;
         ][]=;
     }
     matrix mul(matrix p,matrix q){
         int i,j,k;
         matrix m;
         memset(m.a,,sizeof m.a);
         ;i<=;i++)
             ;j<=;j++)
                 ;k<=;k++)
                     m.a[i][j]=(m.a[i][j]+p.a[i][k]*q.a[k][j])%Mod;
         return m;
     }
     void mfpow(ll p){
         init();
         while(p){
             ) res=mul(base,res);
             base=mul(base,base);
             p>>=;
         }
     }
     int main(){
         int k;
         n=read();
         mfpow(n-);
         c[]=;
         c[]=;
         ;k<=;k++)
             ans=(ans+res.a[][k]*c[k])%Mod;
         cout<<ans<<endl;
         ;
     }
 }
 int main(){
     lys::main();
     ;
 }
 inline ll read(){
     ll k=,f=;
     char c=getchar();
     '){
         if(c=='-')
             f=-;
         c=getchar();
     }
     '){
         k=k*+c-';
         c=getchar();
     }
     return k*f;
 }

---

题目链接[luogu]：

https://www.luogu.org/problem/show?pid=1962