[补档][Lydsy2017年4月月赛]抵制克苏恩

[Lydsy2017年4月月赛]抵制克苏恩

题目

小Q同学现在沉迷炉石传说不能自拔。他发现一张名为克苏恩的牌很不公平。

如果你不玩炉石传说，不必担心，小Q同学会告诉你所有相关的细节。炉石传说是这样的一个游戏，每个玩家拥有一个 30 点血量的英雄，并且可以用牌召唤至多 7 个随从帮助玩家攻击对手，其中每个随从也拥有自己的血量和攻击力。小Q同学有很多次游戏失败都是因为对手使用了克苏恩这张牌，所以他想找到一些方法来抵御克苏恩。他去求助职业炉石传说玩家椎名真白，真白告诉他使用奴隶主这张牌就可以啦。如果你不明白我上面在说什么，不必担心，小Q同学会告诉你他想让你做什么。现在小Q同学会给出克苏恩的攻击力是 K ，表示克苏恩会攻击 K 次，每次会从对方场上的英雄和随从中随机选择一个并对其产生 1 点伤害。现在对方有一名克苏恩，你有一些奴隶主作为随从，每名奴隶主的血量是给定的。如果克苏恩攻击了你的一名奴隶主，那么这名奴隶主的血量会减少 1 点，当其血量小于等于 0 时会死亡，如果受到攻击后不死亡，并且你的随从数量没有达到 7 ，这名奴隶主会召唤一个拥有 3 点血量的新奴隶主作为你的随从；如果克苏恩攻击了你的英雄，你的英雄会记录受到 1 点伤害。你应该注意到了，每当克苏恩进行一次攻击，你场上的随从可能发生很大的变化。小Q同学为你假设了克苏恩的攻击力，你场上分别有 1 点、 2 点、 3 点血量的奴隶主数量，你可以计算出你的英雄受到的总伤害的期望值是多少吗？

INPUT

输入包含多局游戏。

第一行包含一个整数 T (T<100) ，表示游戏的局数。

每局游戏仅占一行，包含四个非负整数 K, A, B和C，表示克苏恩的攻击力是K，你有A个1点血量的奴隶主，B个2点血量的奴隶主，C个3点血量的奴隶主。

保证K是小于50的正数，A+B+C不超过 7 。

OUTPUT

对于每局游戏，输出一个数字表示总伤害的期望值，保留两位小数。

SAMPLE

INPUT

1

1 1 1 1

OUTPUT

0.25

解题报告

这题目真长= =，而且以前我难道玩的是假的炉石么= =

考试时打了一个假的一维数组递推，半分没骗到= =，然而发现正解是四维的= =

正解：

概率DP，克苏恩对英雄造成伤害的概率与仆从的数量有关，我们可以设f[i][j][k][l]表示第i时，仆从一滴血的有j个，两滴血的有k个，三滴血的有l个。

那么，f[i][j][k][l]可以转移到的状态有：

1. 攻击英雄：f[i+1][j-1][k][l]

2. 攻击一个血量为1的仆从： f[i+1][j-1][k][l]（因为一滴血的受到攻击就死了，故不会召唤仆从）

3. 攻击一个血量为2的仆从： f[i+1][j+1][k-1][l]（当j+k+l==7时，无法继续召唤仆从）OR f[i+1][j+1][k-1][l+1]（当j+k+l<7时，可以继续召唤仆从）

4. 攻击一个血量为3的仆从： f[i+1][j][k+1][l-1]ORf[i+1][j][k+1][l]（情况同上）

最后答案就是

剩下的就是代码实现了

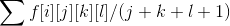
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 inline int read(){
     int sum();
     char ch(getchar());
     for(;ch<''||ch>'';ch=getchar());
     for(;ch>=''&&ch<='';sum=sum*+(ch^),ch=getchar());
     return sum;
 }
 int T;
 int k,a,b,c;
 double f[][][][];
 double ans();
 int main(){
     T=read();
     while(T--){
         memset(f,,sizeof(f));
         k=read(),a=read(),b=read(),c=read();
         f[][a][b][c]=;
         ans=;
         for(int i=;i<k;i++)
             for(int j=;j<=;j++)
                 for(int o=;o<=;o++)
                     for(int l=;l<=;l++){
                         f[i+][j][o][l]+=f[i][j][o][l]*(1.0/(j+o+l+1.0));
                         f[i+][j-][o][l]+=f[i][j][o][l]*(j/(j+o+l+1.0));
                         if(o){
                             if(j+o+l==)
                                 f[i+][j+][o-][l]+=f[i][j][o][l]*(o/(j+o+l+1.0));
                             else
                                 f[i+][j+][o-][l+]+=f[i][j][o][l]*(o/(j+o+l+1.0));
                         }
                         if(l){
                             if(j+o+l==)
                                 f[i+][j][o+][l-]+=f[i][j][o][l]*(l/(j+o+l+1.0));
                             else
                                 f[i+][j][o+][l]+=f[i][j][o][l]*(l/(j+o+l+1.0));
                         }
                     }
         for(int i=;i<=k;i++)
             for(int j=;j<=;j++)
                 for(int o=;o<=;o++)
                     for(int l=;l<=;l++)
                         ans+=f[i][j][o][l]*1.0/(double)(j+o+l+1.0);
         printf("%.2lf\n",ans);
     }
 }

为啥我当时就推出了个一维递推= =