ACM 中 矩阵数据的预处理 && 求子矩阵元素和问题

        我们考虑一个$N\times M$的矩阵数据，若要对矩阵中的部分数据进行读取，比如求某个$a\times b$的子矩阵的元素和，通常我们可以想到$O(ab)$的遍历那个子矩阵，对它的各个元素进行求和。然而当$a$或$b$很大的时候，这样的计算显得太慢，如果要求子矩阵的最大元素和（如Ural 1146），更是简直慢到不能忍。

        于是就想，能不能在读入数据的同时，我就先进行一些预处理，使得到后面进行计算的时候，可以简化一些步骤呢？答案是可以的。
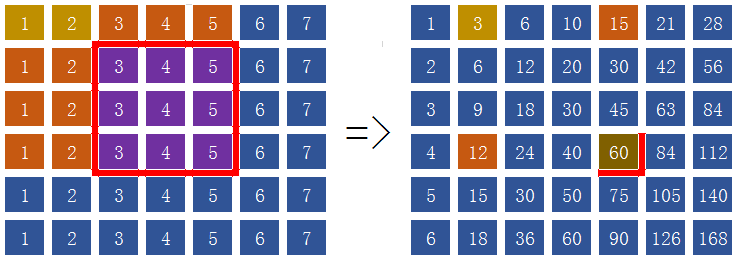
        我们开一个二维数组存放矩阵，第$0$行和第$0$列全都置$0$，真正的矩阵在数组中下标从$1$开始。

        通常对矩阵有两种预处理：

        一种是把矩阵拍扁，即把前一列或前一行加到后一列或后一行上：

按列压缩↑，紫色部分和=棕色部分和-橙色部分和

按行压缩↑，紫色部分和=棕色部分和-橙色部分和

        以按行压缩为例，读入当前元素$t=A_{ij}$后，我们令$B_{ij}=A_{ij}+B_{i-1,j}$，以此类推，当所有数据读入后，预处理即完成，$B_{ij}$表示对于矩阵$A$的第$j$列，从第1行到第$i$行的和。这样我们若想要知道矩阵$A$第$j$列上，从第$p$行到第$q$行的和，直接用$B_{qj}-B_{p-1,j}, (p\leq q)$一步求出，而不需要进行$q-p+1$步计算，那么从左上角$A_{ab}$到右下角$A_{pq}$的子矩阵元素和为$sum$$=$$\sum\limits_{i=a}^{p}\sum\limits_{j=b}^{q}$$A_{ij}$$=$$\sum\limits_{j=b}^{q}$$B_{pj}$$-$$\sum\limits_{j=b}^{q}$$B_{a-1,j}$大大减少了计算量，降低了时间复杂度。

        比较丑的示例代码：

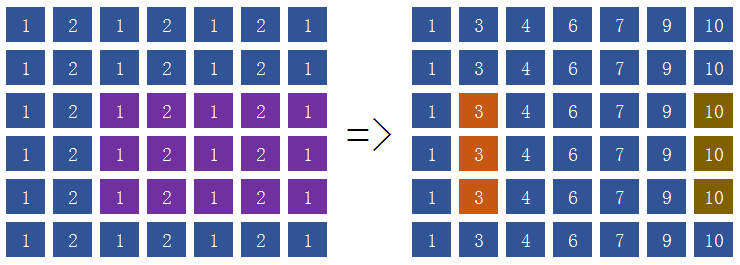
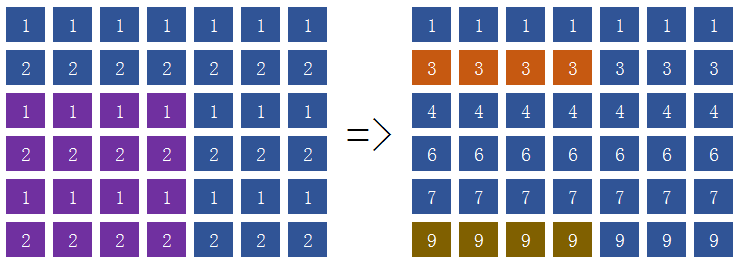
 #include <stdio.h>
 const int N=;
 int matA[N][N], matB[N][N];
 int main()
 {
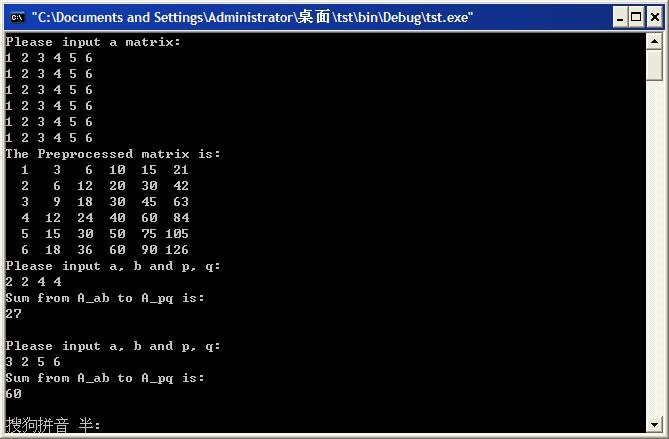
     puts("Please input a matrix:");
     for(int i=; i<N; i++)
         for(int j=; j<N; j++) {
             scanf("%d", matA[i]+j);
             matB[i][j]=matB[i-][j]+matA[i][j];
         }
     puts("The Preprocessed matrix is:");
     for(int i=; i<N; i++)
         for(int j=; j<N; j++)
             printf("%d%c", matB[i][j], j==N-?'\n':' ');

     int a, b, p, q, res;
     while(puts("Please input a, b and p, q:"),
           ~scanf("%d%d%d%d", &a, &b, &p, &q) )
     {
         res=;
         puts("Sum from A_ab to A_pq is:");
         for(int j=b; j<=q; j++)
             res+=matB[p][j]-matB[a-][j];
         printf("%d\n\n", res);
     }
     return ;
 }

        运行结果：

 

       而另一种则是压缩到一个元素上，用$B_{ij}$表示从最左上角元素$A_{11}$到元素$A_{ij}$的和$\sum\limits_{m=1}^{i}\sum\limits_{n=1}^{j}$$A_{mn}$$, $$(i \geq 1, j \geq 1)$：

读入预处理↑，右图紫色块=4+24+30-18=40

        为了保持这一性质，我们在读入当前元素$t=A_{ij}$后，令$B_{ij}$$=$$A_{ij}$$+$$B_{i,j-1}$$+$$B_{i-1,j}$$-$$B_{i-1,j-1}$。当所有数据读入后，预处理即完成。

计算区域和↑，紫色区域和=60-12-15+3=36

        此时我们若想要求出从左上角$A_{ab}$到右下角$A_{pq}$的子矩阵元素和，只需三步计算：$sum$$=$$\sum\limits_{i=a}^{p}\sum\limits_{j=b}^{q}$$A_{ij}$$=$$B_{pq}$$-$$B_{p,b-1}$$-$$B_{a-1,q}$$+$$B_{a-1,b-1}$，即可使时间复杂度降低到常数。

        比较丑的示例代码：

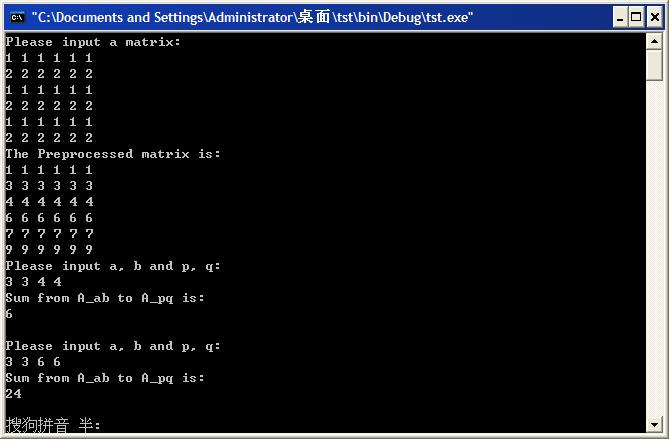
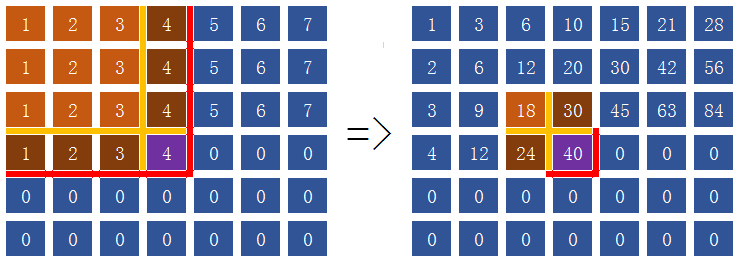
 #include <stdio.h>
 const int N=;
 int matA[N][N], matB[N][N];
 int main()
 {
     puts("Please input a matrix:");
     for(int i=; i<N; i++)
         for(int j=; j<N; j++) {
             scanf("%d", matA[i]+j);
             matB[i][j]=matA[i][j]+matB[i][j-]+matB[i-][j]-matB[i-][j-];
         }
     puts("The Preprocessed matrix is:");
     for(int i=; i<N; i++)
         for(int j=; j<N; j++)
             printf("%3d%c", matB[i][j], j==N-?'\n':' ');

     int a, b, p, q, res;
     while(puts("Please input a, b and p, q:"),
           ~scanf("%d%d%d%d", &a, &b, &p, &q) )
     {
         puts("Sum from A_ab to A_pq is:");
         res=matB[p][q]-matB[p][b-]-matB[a-][q]+matB[a-][b-];
         printf("%d\n\n", res);
     }
     return ;
 }

        运行结果：

By Black Storm（使用为知笔记）