pku 1061 青蛙的约会 扩展欧几里得

青蛙的约会
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 120482 Accepted: 25449
Description

两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它们出发之前忘记了一件很重要的事情，既没有问清楚对方的特征，也没有约定见面的具体位置。不过青蛙们都是很乐观的，它们觉得只要一直朝着某个方向跳下去，总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙，你被要求写一个程序来判断这两只青蛙是否能够碰面，会在什么时候碰面。 
我们把这两只青蛙分别叫做青蛙A和青蛙B，并且规定纬度线上东经0度处为原点，由东往西为正方向，单位长度1米，这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x，青蛙B的出发点坐标是y。青蛙A一次能跳m米，青蛙B一次能跳n米，两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。 
Input

输入只包括一行5个整数x，y，m，n，L，其中x≠y < 2000000000，0 < m、n < 2000000000，0 < L < 2100000000。
Output

输出碰面所需要的跳跃次数，如果永远不可能碰面则输出一行"Impossible"
Sample Input

1 2 3 4 5
Sample Output

4

思路：

根据题意有：

整理得：

所以根据扩展欧几里得我们可以解如下方程：

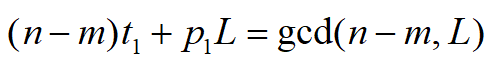
得到初始解t1，但是这不是最后的解，继续变换

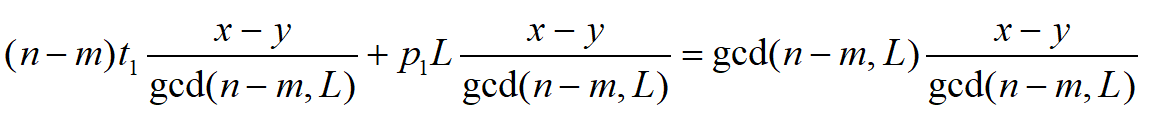
即：

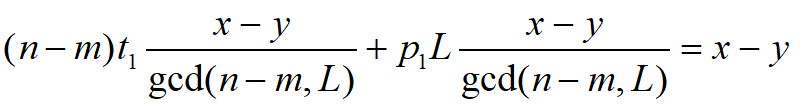
则有：

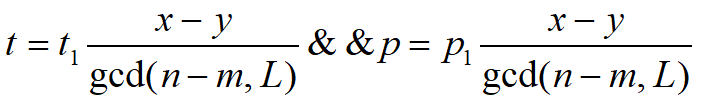
根据不定方程，这里的t还只是特解，变成通解需要表示为（设t₂为通解）：

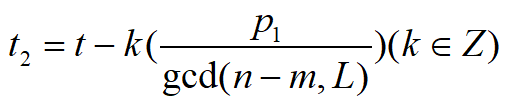
为了保证是最小正解，可以直接通过模运算（加模）获得：

代码：

 #include <iostream>
 using namespace std;
 typedef long long ll;
 ll gcd(ll a, ll b) {if(!b) return a; return gcd(b,a%b);}
 ll exgcd(ll a, ll b, ll &x, ll &y) {
     if(!b) {
         x=;y=;return a;
     }
     ll ans=exgcd(b,a%b,x,y);
     ll temp=x;
     x=y;
     y=temp-a/b*y;
     return ans;
 }
 int main() {
     ios::sync_with_stdio(false);
     ll x,y,m,n,l;
     ll a,b;
     cin>>x>>y>>m>>n>>l;
     int g=exgcd(n-m,l,a,b);
     if((x-y)%g) {
         cout<<"Impossible"<<endl;
         return ;
     }
     ll b3=(x-y)/g,b2=(l)/g;
     ll ans=a*b3;
     ans=(ans%b2+b2)%b2;
     cout<<ans<<endl;
     return ;
 }