Bzoj-2820 YY的GCD Mobius反演,分块

　　题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=2820

　　题意：多次询问，求1<=x<=N, 1<=y<=M且gcd(x,y)为质数有多少对。

　　首先，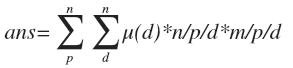   

　　由于这里是多次询问，并且数据很大，显然不能直接求解，需要做如下处理。。

　　整数的除法是满足结合律的，然后我们设T=p*d，有：

　　注意到后面部分是可以预处理出来的，那么整个ans就可以用分块处理来求了，设

　　那么有，考虑当p|x时，根据莫比菲斯mu(x)的性质，px除以其它非p的质数因数都为0，所以g(px)=mu(x)。当p!|x时，除数为p时为mu(x)，否则其它的和为-g(x)，因为这里还乘了一个p所以要变反。然后O(n)预处理下就可以了。。

 //STATUS:C++_AC_3660MS_274708KB
 #include <functional>
 #include <algorithm>
 #include <iostream>
 //#include <ext/rope>
 #include <fstream>
 #include <sstream>
 #include <iomanip>
 #include <numeric>
 #include <cstring>
 #include <cassert>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <bitset>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <ctime>
 #include <list>
 #include <set>
 //#include <map>
 using namespace std;
 //#pragma comment(linker,"/STACK:102400000,102400000")
 //using namespace __gnu_cxx;
 //define
 #define pii pair<int,int>
 #define mem(a,b) memset(a,b,sizeof(a))
 #define lson l,mid,rt<<1
 #define rson mid+1,r,rt<<1|1
 #define PI acos(-1.0)
 //typedef
 typedef long long LL;
 typedef unsigned long long ULL;
 //const
 const int N=;
 const int INF=0x3f3f3f3f;
 const int MOD=,STA=;
 const LL LNF=1LL<<;
 const double EPS=1e-;
 const double OO=1e15;
 const int dx[]={-,,,};
 const int dy[]={,,,-};
 const int day[]={,,,,,,,,,,,,};
 //Daily Use ...
 inline int sign(double x){return (x>EPS)-(x<-EPS);}
 template<class T> T gcd(T a,T b){return b?gcd(b,a%b):a;}
 template<class T> T lcm(T a,T b){return a/gcd(a,b)*b;}
 template<class T> inline T lcm(T a,T b,T d){return a/d*b;}
 template<class T> inline T Min(T a,T b){return a<b?a:b;}
 template<class T> inline T Max(T a,T b){return a>b?a:b;}
 template<class T> inline T Min(T a,T b,T c){return min(min(a, b),c);}
 template<class T> inline T Max(T a,T b,T c){return max(max(a, b),c);}
 template<class T> inline T Min(T a,T b,T c,T d){return min(min(a, b),min(c,d));}
 template<class T> inline T Max(T a,T b,T c,T d){return max(max(a, b),max(c,d));}
 //End

 LL sum[N],g[N];
 int isprime[N],mu[N],prime[N];
 int cnt;
 int T,n,m;

 void Mobius(int n)
 {
     int i,j;
     //Init isprime[N],mu[N],prime[N],全局变量初始为0
     cnt=;mu[]=;
     for(i=;i<=n;i++){
         if(!isprime[i]){
             prime[cnt++]=i;
             mu[i]=-;
             g[i]=;
         }
         for(j=;j<cnt && i*prime[j]<=n;j++){
             isprime[i*prime[j]]=;
             if(i%prime[j]){
                 mu[i*prime[j]]=-mu[i];
                 g[i*prime[j]]=mu[i]-g[i];
             }
             else {
                 mu[i*prime[j]]=;
                 g[i*prime[j]]=mu[i];
                 break;
             }
         }
     }
     for(i=;i<=n;i++)sum[i]=sum[i-]+g[i];
 }

 int main(){
  //   freopen("in.txt","r",stdin);
     int i,j,la;
     LL ans;
     Mobius();
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d",&n,&m);

         if(n>m)swap(n,m);
         ans=;
         for(i=;i<=n;i=la+){
             la=Min(n/(n/i),m/(m/i));
             ans+=(sum[la]-sum[i-])*(n/i)*(m/i);
         }

         printf("%lld\n",ans);
     }
     return ;
 }