最短路径算法之一——Floyd算法

Floyd算法

　　Floyd算法可以用来解决任意两个顶点之间的最短路径问题。

　　核心公式为：

　　　　　　Edge[i][j]=Min{Edge[i][j],Edge[i][k]+Edge[k][j]}。

　　即通过对i,j两个顶点之间插入顶点后比较路径的大小来进行松弛。

　　首先我们来定义一个二维数组Edge[MAXN][MAXN]来存储图的信息。

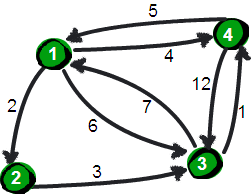
　　　　这个图的Edge数组初始化以后为

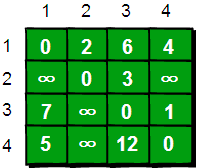
相当于任意两点之间不允许经过其他点时的距离情况。

Code1:

 //经过1号顶点
 for(i=;i<=n;i++)
     for(j=;j<=n;j++)
         if (e[i][j] > e[i][]+e[][j])  e[i][j]=e[i][]+e[][j];

这里表示允许一号顶点作为中间点来松弛距离，并保存松弛完的结果。

Code2：

 //经过2号顶点
 for(i=;i<=n;i++)
     for(j=;j<=n;j++)
         if (e[i][j] > e[i][]+e[][j])  e[i][j]=e[i][]+e[][j];

允许一号顶点和二号顶点作为中间点来松弛，并保存。(不是必定会松弛！)

。。。。。

Floyd核心代码：

 for(k=;k<=n;k++)
     for(i=;i<=n;i++)
         for(j=;j<=n;j++)
             if(e[i][j]>e[i][k]+e[k][j])
                  e[i][j]=e[i][k]+e[k][j];

这段代码的基本思想就是：最开始只允许经过1号顶点进行中转，接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从i号顶点到j号顶点只经过前k号点的最短路程。

时间复杂度：O(n^3)

部分图片文字摘自于啊哈磊的blog。