梯度下降算法(Gradient descent)GD

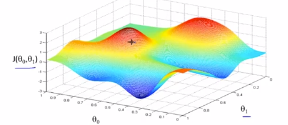
1.我们之前已经定义了代价函数J，可以将代价函数J最小化的方法，梯度下降是最常用的算法，它不仅仅用在线性回归上，还被应用在机器学习的众多领域中，在后续的课程中，我们将使用梯度下降算法最小化其他函数，而不仅仅是最小化线性回归的代价函数J。本节课中，主要讲用梯度下降的算法来最小化任意的函数J，下图是我们的问题：

　　

　　(1)梯度下降的思路：

　　　　给定θ0和θ1的初始值，首先将θ0和θ1初始化为0，在梯度下降中我们要做的是不停的改变θ0和θ1，来使得J(θ0,θ1)变小，直到我们找到J的值的最小值或者局部最小值。

　　　　我们从θ0和θ1的某个值出发，对θ0和θ1赋以初值，就是对应于从下面这个函数的表面上某个点出发，一般情况下降θ0和θ1赋初值为0。

　　　　

　　(2)梯度下降算法：

　　

　　　　我们要更新参数θj，为θj减去α乘以这一部分，接下来详细解释该公式：

　　　　(1)赋值：符号 := 表示赋值，这是一个赋值运算符。具体的说，如果写成a:=b，在计算机中，表示不管a的原始值是是什么，将b赋值给a，这意味着我们设定a等于b的值，这就是赋值。

　　　　(2)α：α表示学习率，用来控制在梯度下降的时候，我们迈出多大的步子，α如果很大，那么梯度就下降的很迅速，我们就会用大步子下山；如果α值比较小，我们就会迈着很小的碎步下山

　　　　(3)θ0和θ1的更新，对于：

　　

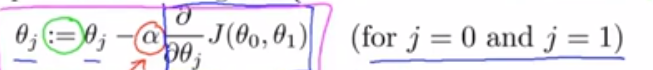
　　我们需要同时更新θ0和θ1，在这个式子中，就是讲θ0减去某项，将θ1减去某项，实现的方法是：计算右边的部分，对θ0和θ1进行计算，然后同时更新θ0和θ1，下面是正确的同步更新的方法。