NOIP2017 Day2 T1 奶酪(并查集)

题目描述

现有一块大奶酪，它的高度为 hhh ，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中，奶酪的下表面为z=0z = 0z=0 ，奶酪的上表面为z=hz = hz=h 。

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在不破坏奶酪的情况下，能否利用已有的空洞跑到奶酪的上表面去?

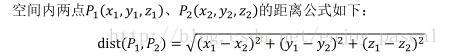
输入输出格式

输入格式：

每个输入文件包含多组数据。

输入文件的第一行，包含一个正整数 T ，代表该输入文件中所含的数据组数。

接下来是 T 组数据，每组数据的格式如下：第一行包含三个正整数 n,h 和 r ，两个数之间以一个空格分开，分别代表奶酪中空洞的数量，奶酪的高度和空洞的半径。

接下来的 n 行，每行包含三个整数 x,y,z ，两个数之间以一个空格分开，表示空洞球心坐标为(x,y,z) 。

输出格式：

输出文件包含 T 行，分别对应 T 组数据的答案，如果在第 i 组数据中，Jerry 能从下表面跑到上表面，则输出Yes，如果不能，则输出No （均不包含引号）。

输入输出样例

输入样例#1：

输出样例#1：

Yes

No

Yes

说明

【输入输出样例 1 说明】

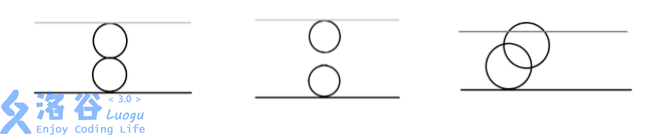
第一组数据，由奶酪的剖面图可见：

第一个空洞在（0，0，0）与下表面相切

第二个空洞在（0，0，4）与上表面相切两个空洞在（0，0，2）相切

输出 Yes

第二组数据，由奶酪的剖面图可见：

两个空洞既不相交也不相切

输出 No

第三组数据，由奶酪的剖面图可见：

两个空洞相交且与上下表面相切或相交

输出 Yes

【数据规模与约定】

对于 20%的数据，n = 1，1 ≤ h , r ≤ 10,000，坐标的绝对值不超过 10,000。
对于 40%的数据，1 ≤ n ≤ 8， 1 ≤ h , r ≤ 10,000，坐标的绝对值不超过 10,000。
对于80%的数据，1 ≤ n ≤ 1,000， 1 ≤ h , r ≤ 10,000，坐标的绝对值不超过10,000。
对于 100%的数据，1 ≤ n ≤ 1,000，1 ≤ h , r ≤ 1,000,000,000，T ≤ 20，坐标的绝对值不超过 1,000,000,000。

一道并查集的裸题，注意数据大小，要开long long。为了避免被卡精度，将公式转换。

dist (P1,P2) = sqrt[(x1-x2)^2+(y1-y2)^2+(z1-z2)^2]

dist(P1,P2)^2=(xi-x2)^2+(y1-y2)^2+(z1-z2)^2

这样我们就可以避免被卡精度。

 #include<iostream>

 #include<cstdio>

 #include<cstring>

 #include<cmath>

 #include<algorithm>

 #define LL long long

 using namespace std;

 LL n,h,r;

 LL x[],y[],z[],sum[],fa[],ul[],ll[];

 LL a[][],dis[][];

 LL read()

 {

     LL x=,w=;char ch=getchar();

     while(ch>''||ch<'') {if(ch=='-')w=-;ch=getchar();}

     while(ch>=''&&ch<='') x=(x<<)+(x<<)+ch-'',ch=getchar();

     return x*w;

 }

 LL gfa(LL x)

 {

     if(x==fa[x]) return x;

     return fa[x]=gfa(fa[x]);

 }

 void work20();

 void work();

 int main()

 {

     LL t;

     t=read();

     for(LL w=;w<=t;w++)

     {

         n=read();h=read();r=read();

         for(LL i=;i<=n;i++)

         fa[i]=i;

         if(n==) work20();

         else work();

     }

     return ;

 }

 void work20()

 {

     LL x,y,z;

     x=read();y=read();z=read();

     if(z-r<=&&z+r>=h)

     {

         printf("Yes\n");

     }

     else printf("No\n");

 }

 void work()

 {

     LL d,flag=;

     LL cnt1=,cnt2=;

     for(LL i=;i<=n;i++)

     {

         x[i]=read();y[i]=read();z[i]=read();

         sum[i]=x[i]*x[i]+y[i]*y[i]+z[i]*z[i];

     }

     for(LL i=;i<=n;i++)

     {

         for(LL j=;j<i;j++)

         {

             LL xx=gfa(i),yy=gfa(j);

             if(xx!=yy)

             {

                 d=sum[i]+sum[j]-*(x[i]*x[j]+y[i]*y[j]+z[i]*z[j]);

                 if(d<=*r*r)

                 {

                     fa[xx]=yy;

                 }

             }

         }

         if(z[i]-r<=&&z[i]+r>=h) flag=;

         if(z[i]-r<=) ll[++cnt1]=i;

         if(z[i]+r>=h) ul[++cnt2]=i;

     }

     if(!flag)

     for(LL i=;i<=cnt1;i++)

     {

         for(LL j=;j<=cnt2;j++)

         {

             LL xx=gfa(ll[i]),yy=gfa(ul[j]);

             if(xx==yy)

             {

                 flag=;

                 break;

             }

         }

         if(flag==) break;

     }

     if(flag==) printf("Yes\n");

     else printf("No\n");

 }