UVA10779 Collectors Problem 【迁移自洛谷博客】

这是一道不错的练最大流建模的基础题。
这种题目审题是关键。
Bob’s friends will only exchange stickers with Bob, and they will give away only
duplicate stickers in exchange with different stickers they don’t possess.
意思就是说，Bob的朋友们只会和Bob交换贴纸，并且呢，他们只会赠送给Bob他们有的重复的的贴纸，以换取他们没有的贴纸。
上面还有一段话，But Bob is clever: he has realized that in some cases it is good for him to trade one of his duplicate stickers for a sticker he already possesses.就是说，Bob他可能会有自己重复的贴纸去换他已经有的贴纸。（这样就可以再用这一张贴纸去换其他他没有的贴纸了）

题目问的是Bob最多可以得到多少贴纸。

很明显，根据以往的经验，这是一个网络流的模型。我们应该把所有的人，所有的贴纸都用一个点来表示一下。任何贴纸之间应该怎么建边呢？ 首先，把一个人（Bob除外），向他可以交换给别人的贴纸（数量>=2）上建边，容量应该为他所拥有此类贴纸数量-1。

然后也可以把一个贴纸向所有不具有它的人连一条边，容量为1（因为每种贴纸一个人只会要一次）,表示把这个贴纸交换过来了。这样一来，我们每流过一个点，一定是进来一次，出来一次，可以很好地表示一次交换。

但是这个成立前提是什么呢？这些贴纸肯定是从Bob开始交换的，也是最后流回Bob的手里的。那么，Bob本人也应该向她所拥有的贴纸建边，边权为他拥有的这类贴纸的数量。为什么不用减1呢？这个问题我们留到后面来解决。

我们还需要再建一个点T，让所有的贴纸都指向T，边权为1。因为每一类贴纸只算一次。我们就可以用从Bob到这个点T的最大流表示Bob可以收集到的贴纸最多有多少类了。其实T这个点，也是用来表示Bob这个人的另一个点。

现在让我们汇过来看刚刚那一个问题。因为Bob的贴纸种类，最终是通过刚刚我们建的那个点T来统计的，所以我们必须把这个留下的贴纸也流过去。就算这个贴纸被换成了其他贴纸了，那也不会影响结果——因为我们建立的这个网络，不会让一类贴纸流到两次到T的，因此即使那个贴纸被换成了其他贴纸，这个贴纸还是唯一的，不会影响总的种类数。

为了便于大家理解，我来画个图。

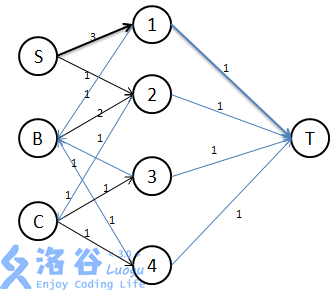
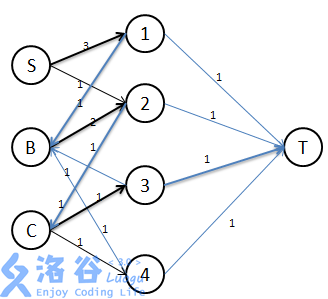
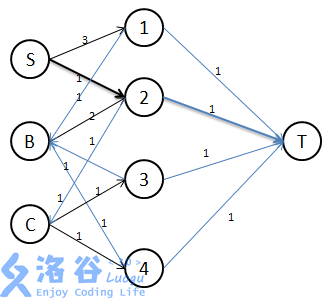
上面三个图，是样例二的模型。其中S是Bob，BC是其他两个人。1234是四种贴纸（题目说有5中，但第五种没有出现）。为了便于分清边的方向，从两边到中间的边是黑色的，从中间到两边的是蓝色的。
每个图加粗的边都是一个单位的流，流一和流三这样从S流到T可以很好地表示Bob本来就有这样的一个贴纸。流二则可以很形象地表示Bob把一张贴纸1和B换来一个贴纸2，有把这个贴纸2从C出换来贴纸3。

这样的话，每一个单位的流，就表示一种贴纸的来龙去脉，如此，最大流是几，就可以表示Bob最多可以收集到多少种贴纸。

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;

const int maxn=10+7,maxm=25+7,INF=0x7f7f7f7f;
int Test,Cas,n,m,x,y,S,T;
int cnt[maxm];

int head[maxn+maxm],tot=-1;
struct Edge{int u,v,flow,ne;}g[maxm*maxn<<4];
inline void addedge(int x,int y,int z){
    g[++tot].u=x;g[tot].v=y;g[tot].flow=z;g[tot].ne=head[x];head[x]=tot;
    g[++tot].u=y;g[tot].v=x;g[tot].flow=0;g[tot].ne=head[y];head[y]=tot;
}

int cur[maxn+maxm],dist[maxn+maxm];queue<int>q;
bool bfs(int s,int t){
    memset(dist,0x7f,sizeof(dist));dist[s]=0;q.push(s);for(register int i=S;i<=T;++i)cur[i]=head[i];
    while(!q.empty()){int x=q.front();q.pop();for(register int i=head[x];~i;i=g[i].ne)if(g[i].flow&&dist[g[i].v]==INF)dist[g[i].v]=dist[x]+1,q.push(g[i].v);}
    return dist[t]<INF;
}
int dfs(int x,int t,int a){
    if(x==t||!a)return a;int flow=0,f;
    for(register int &i=cur[x];~i;i=g[i].ne)if(dist[g[i].v]==dist[x]+1&&(f=dfs(g[i].v,t,min(a,g[i].flow)))){g[i].flow-=f;g[i^1].flow+=f;flow+=f;a-=f;if(!a)break;}
    return flow;
}
inline int Dinic(int s,int t){int ans=0;while(bfs(s,t))ans+=dfs(s,t,INF);return ans;}
//上面是Dinic部分，不用说了吧
void Clear(){tot=-1;memset(head,-1,sizeof(head));}

void Init(){
	Clear();scanf("%d%d",&n,&m);S=1,T=n+m+1;
	for(register int i=1;i<=n;++i){
		scanf("%d",&x);memset(cnt,0,sizeof(cnt));for(register int j=1;j<=x;++j){scanf("%d",&y);++cnt[y];}//cnt用来统计这个人有每种贴纸多少张
		if(i==1)for(register int j=1;j<=m;++j){if(cnt[j])addedge(S,j+n,cnt[j]);}//1就是Bob，这里把Bob向他有的贴纸建边
		else for(register int j=1;j<=m;++j)if(cnt[j]>1)addedge(i,j+n,cnt[j]-1);else if(!cnt[j])addedge(j+n,i,1);//如果这个人有这种贴纸多于1张，就可以用来和别人交换其他贴纸，因此和这种贴纸建边。否则，若此人没有这种贴纸，就可以从别人那里获得，就让那种贴纸向他建边
	}
	for(register int i=1;i<=m;++i)addedge(i+n,T,1);//每种贴纸向终点建边
}

void Work(){
	printf("Case #%d: %d\n",++Cas,Dinic(S,T));
}

int main(){
	scanf("%d",&Test);
	while(Test--){
		Init();
		Work();
	}
}

——发表于2018-04-24 15:01:53