【leetcode】891. Sum of Subsequence Widths

题目如下：

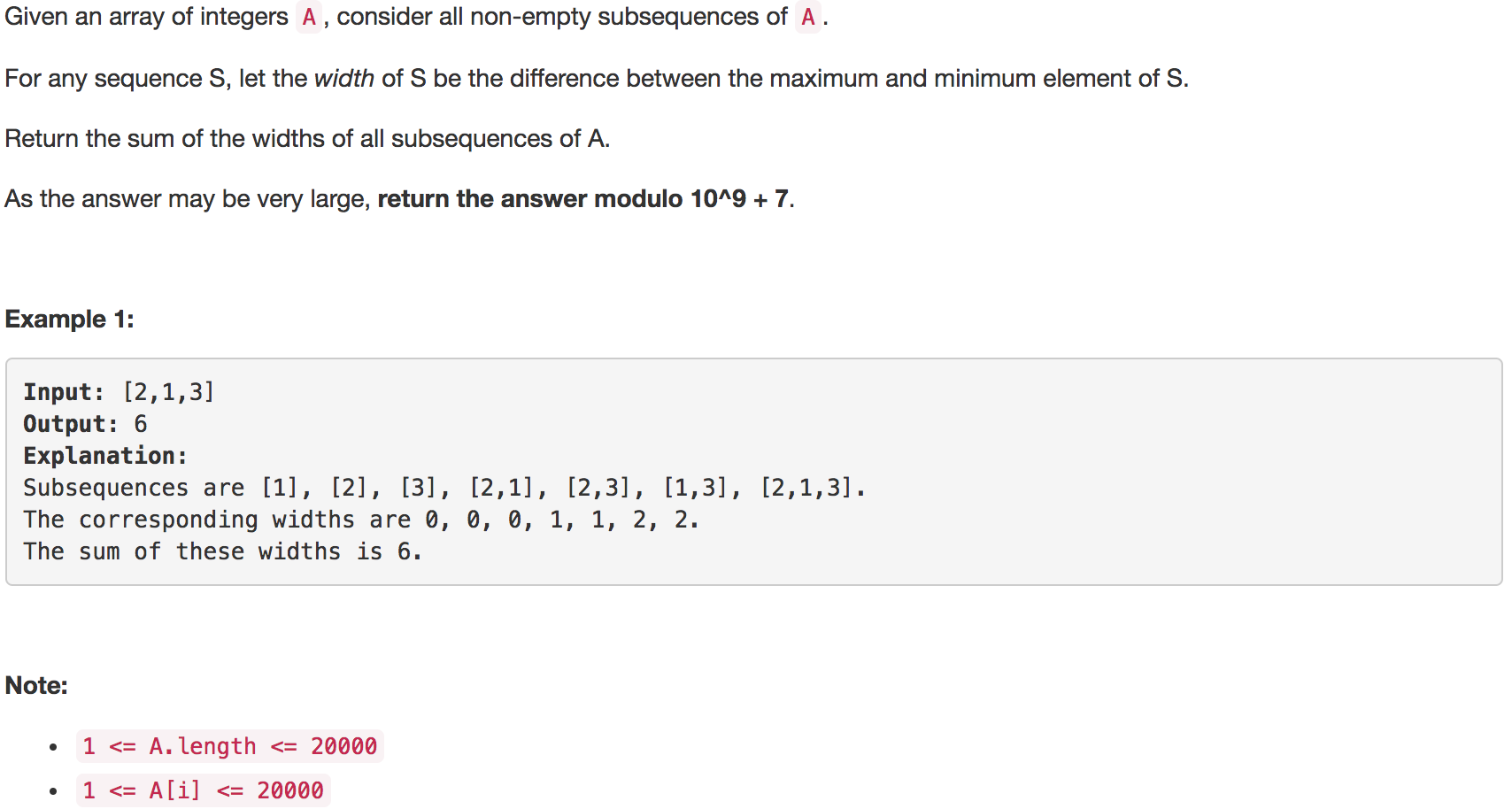
解题思路：题目定义的子序列宽度是最大值和最小值的差，因此可以忽略中间值。首先对数组排序，对于数组中任意一个元素，都可以成为子序列中的最大值和最小值而存在。例如数组[1,2,3,4,5,6]，对于元素3来说，由左边[1,2]组成的所有子序列都可以以3为最大值的，而右边[4,5,6]组成的所有子序列都可以以3为最小值。根据排列组合的原理：[1,2]可以组成的子序列个数为C(2,1) + C(2,2) ，而[4,5,6]可以组成的子序列个数为C(3,1) + C(3,2) + C(3,3) ，同样根据组合计算定律，C(n,1) + C(n,2) + ...... + C(n,n) = 2^n - 1。因为以3为最大值是做被减数，以3为最小值是做减数，因此以3作为最大/最小值的所有子序列的和宽度和就是：(2 ^ 2 - 1)* 3 - (2 ^ 3-1)*3 。同理，也可以求出其他元素的宽度和，并最终求出总宽度和。根据组合的对称性，C(n,m) = C(n,n-m)，因此只需要遍历一半的数组长度即可。

代码如下：

class Solution(object):
    def sumSubseqWidths(self, A):
        """
        :type A: List[int]
        :rtype: int
        """
        A.sort()
        res = 0
        l = 1
        r = pow(2, len(A) - 1)
        for i in range(len(A)/2):

            res += l * A[i]
            res -= r * A[i]

            res += r * A[len(A)-i-1]
            res -= l * A[len(A) - i - 1]

            l *= 2
            r /= 2
        return res % (pow(10,9) + 7)