【leetcode】1105. Filling Bookcase Shelves

题目如下：

We have a sequence of books: the i-th book has thickness books[i][0] and height books[i][1].

We want to place these books in order onto bookcase shelves that have total width shelf_width.

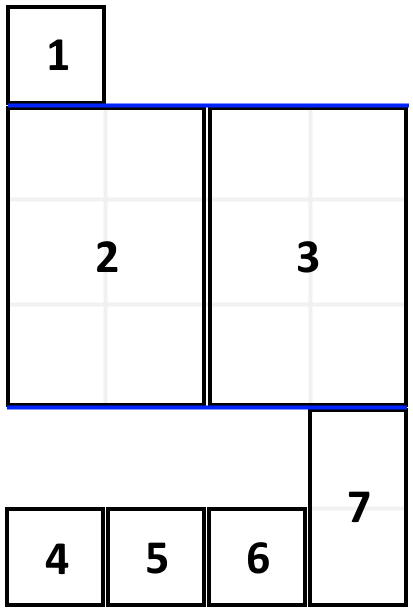
We choose some of the books to place on this shelf (such that the sum of their thickness is <= shelf_width), then build another level of shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down.  We repeat this process until there are no more books to place.

Note again that at each step of the above process, the order of the books we place is the same order as the given sequence of books.  For example, if we have an ordered list of 5 books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.

Return the minimum possible height that the total bookshelf can be after placing shelves in this manner.

Example 1:

Input: books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelf_width = 4
Output: 6
Explanation:
The sum of the heights of the 3 shelves are 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.

Constraints:

• 1 <= books.length <= 1000
• 1 <= books[i][0] <= shelf_width <= 1000
• 1 <= books[i][1] <= 1000

解题思路：比起大神们的算法，我的dp算法多了一维，差距还是很大的。记dp[i][j] = v 表示第i本书是第j层的最后一本书时，书架第0层到第j层的高度的最小值是v。如果第j-1层的最后一本书是k，那么有dp[i][j] = min(dp[i][j],dp[k][j-1] + max(books[k+1] ~books[i])。有了这个状态转移方程，接下来就是求k的可能取值，每一层至少要有一本书，所以k的最大值只能是i-1,最小值则要通过计算得出，详见代码。

代码如下：

class Solution(object):
    def minHeightShelves(self, books, shelf_width):
        """
        :type books: List[List[int]]
        :type shelf_width: int
        :rtype: int
        """
        dp = [[float('inf') for i in range(len(books))] for i in range(len(books))]
        dp[0][0] = books[0][1]

        width = 0
        level = 0
        level_list_per_item = []
        for i in range(len(books)):
            if width + books[i][0] <= shelf_width:
                level_list_per_item.append(level)
                width += books[i][0]
            else:
                level += 1
                level_list_per_item.append(level)
                width = books[i][0]

        for i in range(1,len(books)):
            for j in range(level_list_per_item[i],i+1):
                if j > 0:
                    dp[i][j] = min(dp[i][j],dp[i-1][j-1] + books[i][1])
                row_width = books[i][0]
                row_max_height = books[i][1]
                for k in range(i-1,j-2,-1):
                    if row_width + books[k][0] <= shelf_width:
                        row_width += books[k][0]
                        row_max_height = max(row_max_height,books[k][1])
                        if k == 0:
                            dp[i][j] = min(dp[i][0] ,row_max_height)
                            continue
                        dp[i][j] = min(dp[i][j],dp[k-1][j-1]+ row_max_height)
                    else:
                        break
        #print dp
        return min(dp[-1])