jzoj6404. 【NOIP2019模拟11.04】B

题目描述

Description

Input

从文件b.in中读入数据. 第丬行三个正整数 n, m, K. 接下来 n 行每行 m 个正整数, 表示矩阵A.

Output

输出到文件b.out中. 不行, 两个数分别表示机大值和和.

Sample Input

3 5 2

1 5 3 3 3

4 1 3 3 4

4 2 4 4 3

Sample Output

4 20

Data Constraint

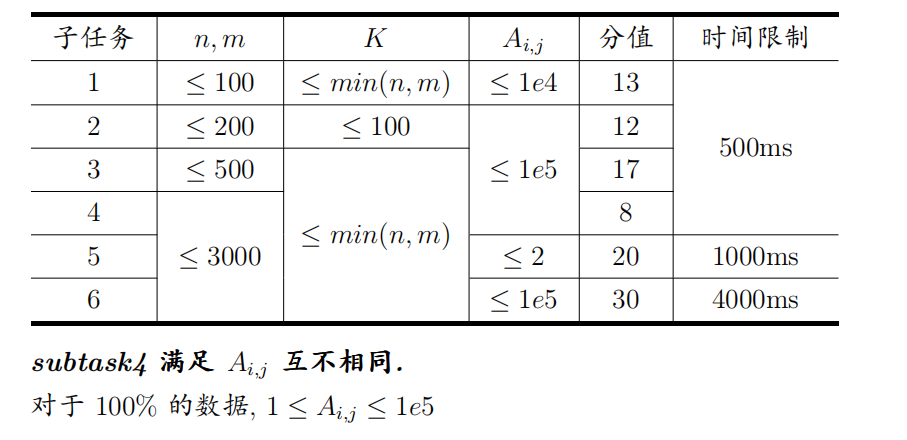
题解

从左往右扫，维护一个宽为K的区域

对于一个位置(i,j)，求出bz[i][j]表示(i,j+1)~(i,j+K)之中是否有a[i][j]

那么在求以每个点为左上角时，区域内的点的纵坐标不会影响到结果

所以维护每种权值出现的行，0-->1就直接加，1-->0就是在删掉一个bz[i][j]=0的值时

只需要在删/加的时候求出一种值上的一个位置的前/后继

可以线段树，也可以用bitset的_Find_next()

然而NOIP应该不能用

所以显然手写bitset（

code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define change(T,t) b[T][(t)/64]^=p[(t)%64]
#define pd(T,t) (b[T][(t)/64]&p[(t)%64])
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define low(x) ((x)&-(x))
#define Len 100000
using namespace std;

unsigned long long p[64];
int a[3001][3001];
int f[3002][3001];
bool bz[3001][3001];
int num[100001];
unsigned long long b[200001][47];
char st[72000001];
char *Ch=st;
int N,n,m,K,i,j,k,l;
long long ans1,ans2;

int getint()
{
	int x=0;

	while (*Ch<'0' || *Ch>'9') *++Ch;
	while (*Ch>='0' && *Ch<='9') x=x*10+(*Ch-'0'),*++Ch;

	return x;
}

int find(int T,int t)
{
	int i,j,s=t/64;t%=64;
	unsigned long long S=b[T][s];

	if (t<63)
	S>>=t+1;
	else
	S=0;

	if (S)
	return floor(log2(low(S))+0.1)+64*s+t+1;

	fo(i,s+1,N)
	if (b[T][i])
	return floor(log2(low(b[T][i]))+0.1)+64*i;

	return -1;
}

void add(int I,int i,int j,int s)
{
	int k,l,L,R;

	change(a[i][j],i);
	change(a[i][j]+Len,n-i+1);

	k=find(a[i][j]+Len,n-i+1);if (k!=-1) k=n-k+1;
	l=find(a[i][j],i);

	L=max(i-K+1,1);
	R=i;

	if (k!=-1) L=max(L,k+1);
	if (l!=-1) R=min(R,l-K);

	if (L<=R)
	f[L][I]+=s,f[R+1][I]-=s;
}

int main()
{
//	freopen("b53.in","r",stdin);
	freopen("b.in","r",stdin);
	freopen("b.out","w",stdout);

	fread(st,1,72000001,stdin);

	p[0]=1;
	fo(i,1,63)
	p[i]=p[i-1]<<1;

	n=getint(),m=getint(),K=getint();N=n/64;
	fo(i,1,n)
	{
		fo(j,1,m)
		a[i][j]=getint();
	}

	memset(num,127,sizeof(num));

	fo(i,1,n)
	{
		fd(j,m,1)
		{
			bz[i][j]=(num[a[i][j]]-j)<=K;
			num[a[i][j]]=j;
		}

		fo(j,1,m)
		num[a[i][j]]=2133333333;
	}

	fo(j,1,K)
	{
		fo(i,1,n)
		if (!pd(a[i][j],i))
		add(1,i,j,1);
	}
	fo(j,2,m-K+1)
	{
		fo(i,1,n)
		f[i][j]=f[i][j-1];

		fo(i,1,n)
		{
			if (!pd(a[i][j+K-1],i))
			add(j,i,j+K-1,1);
			if (!bz[i][j-1])
			add(j,i,j-1,-1);
		}
	}

	fo(i,1,n-K+1)
	{
		fo(j,1,m-K+1)
		{
			f[i][j]+=f[i-1][j];

			ans1=max(ans1,f[i][j]);
			ans2+=f[i][j];
		}
	}
	printf("%lld %lld\n",ans1,ans2);

	fclose(stdin);
	fclose(stdout);

	return 0;
}