【一个蒟蒻的挣扎】LCA （倍增）

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
struct edge{
    int next,to;
    edge(){
    }
    edge(int a,int b){
        next=a; to=b;
    }
}E[];//建一个图……
int f[][],dep[],first[],tot;
int n,m,root;
void add_to_edge(int x,int y)
{
    E[++t]=edge(first[x],y);
    first[x]=t;
}//连边（无向图连两次哦）
void dfs(int x,int fa)
{
    f[x][]=fa;
    dep[x]=dep[fa]+;
    //初始化 , 它的深度是它父亲的深度+1，x 往上倍增 2^0 层 是它的父亲
    int k=ceil(log(dep[x])/log());//倍增上限
    for (int i=; i<=k; i++)
    {
        f[x][i]=f[f[x][i-]][i-];
    }//f数组存预处理的值，f[x][i]存的是x向上倍增
    for (int i=first[x]; i; i=E[i].next)
    {
        int pos=E[i].to;
        if (pos!=fa)//防止死循环，由于是存了两次所以E[i].to会连向它的父亲
        dfs(pos,x);
    }
}//预处理
int n,m,root;
void LCA()
{
    if (dep[x]<dep[y]) swap(x,y);
    int k1=dep[x]-dep[y];
    int k2=ceil((log(n))/log());
    for (int i=; i<=k2; i++)
    {
        if (k1&(<<i))
        x=fa[x][i];
    }//向上跳！！
    if (x==y) return x;//两者在同一层并且相等那么x 就是它们的共同祖先
    int k3=(log(dep[x])/log());
    for (int i=k3; i>=; i--)
    {
        if (f[x][i]!=f[y][i])
        {
            x=f[x][i]; y=f[y][i];
        }//倍增
    }
    return f[x][];
}
int main()
{
    cin>>n>>m>>root;
    for (int i=; i<=m; i++)
    {
        int x,y;
        cin>>x>>y;
        add_to_edge(x,y);
        add_to_edge(y,s);
    }
    dfs(root,);

}

还是济南集训的内容，让人头秃（不得不说两个老师讲了两遍我勉勉强强才搞懂一点点）

---

首先来看：

LCA的含义

Least  Common  Ancestors

LCA就是最近公共祖先，至于它的含义，我觉得例题写的看起来会更清楚，请看：

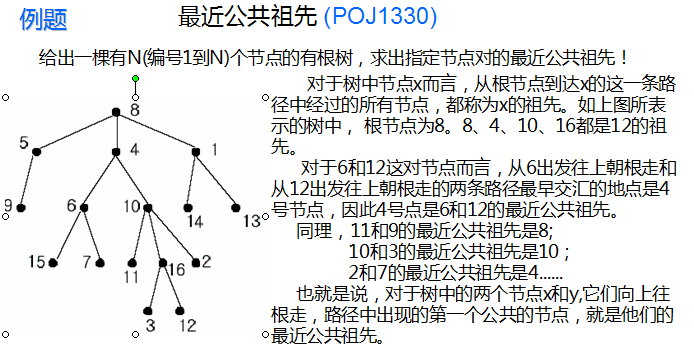
好的，明白了它的含义后，我们很容易想到朴素算法：

询问(x,y)的最近公共祖先，可以先向上枚举x的所有祖先，保存在数组Anc[]中。然后以相同的方法向上枚举y的所有祖先，当第一次发现有y的某个祖先k出现在Anc[]中，则输出k，算法结束。

 此时，每次查询复杂度为O( N )

（TLE警告哦）

那么其他方法呢，请看，这里介绍两种，树上倍增，与树链剖分（会在下一篇博客里写到）

---

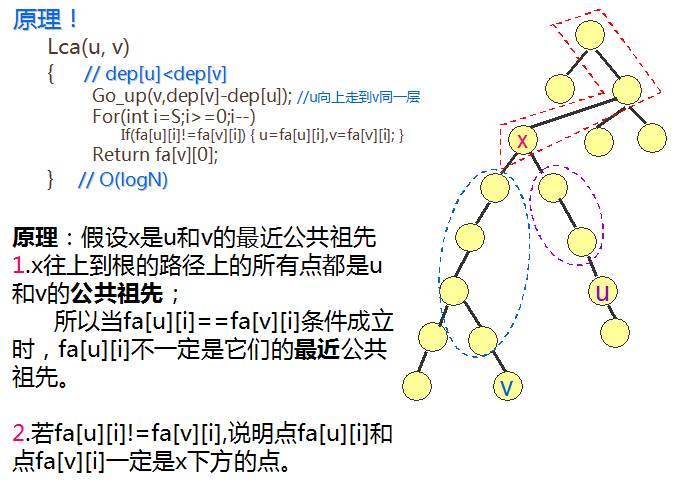
树上倍增算法

核心思想：

• 令F[x][n]表示x的2^n级祖先是谁.
• 所以：F[x][n] = F[F[x][n – 1]][n – 1].

• 对于两个点x, y.，求他们的LCA
• 先把x, y提到同一高度.（方便向上进行倍增）
• N从大到小枚举.（从高往低跳）
• 查询F[x][n], F[y][n]是不是相等（比较倍增后的祖先，防止误判）
• 如果是的话说明n太大了，把n改小点.（最近公共祖先的祖先一定是他们的共同祖先）
• 不是的话就说明n不大，可以把x, y上移.（这个很容易理解吧）

 原理，如下图（图片来自老师的ppt）（它其实应该有个动图然而我不知道动图怎么传）：

 看明白思路了吗，思路还是可以懂得吧，那我们来看代码，理解代码基本就能写了！

（不过我之前也始终看不明白代码就是了，思路都懂代码不会打，我可真是个小垃圾哦）

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
const int maxn = ;
const int maxe = ;
int n,m,root;

struct line
{
    int from,to;
    line(){}//空构造函数 line p;
    line(int A,int B){
        //构造函数 line L=line(1,2);
        from=A;to=B;
    }
}edge[maxe];
//上面是新建一个树

int last[maxn],_next[maxe],e;
//last[x]表示以x为起点的最后一条边（的编号）
//_next[i]表示与第i条边起点相同的上一条边（的编号） 

void add_edge(int x,int y)
{
    edge[++e]=line(x,y);
    _next[e]=last[x];
    last[x]=e;
}
//存边 

int Fa[maxn][],Dep[maxn];

void dfs(int x,int fa)
{
    int i,k,y;
    Fa[x][]=fa;//当前节点x的父亲节点fa
    Dep[x]=Dep[Fa[x][]]+; //x的深度是它父亲节点的深度+1
    //记录当前节点的深度
    k=ceil(log(Dep[x])/log());  //ceil函数是向上取整
    //x往上倍增的上限
    for(i=;i<=k;i++)Fa[x][i]=Fa[Fa[x][i-]][i-];
     //倍增计算祖先 ，记录
    for(int i=last[x];i;i=_next[i])//枚举与x相邻的边
    {
        int v=edge[i].to;
        if(v!=fa)dfs(v,x);
    }
}

int LCA(int x,int y)
{
    int i,k,s;
    s=ceil(log(n)/log());                 //该树倍增最大可能的上限
    if(Dep[x]<Dep[y])swap(x,y);      //交换x和y的值
    /////////////x往上走k层，让x与y处于同一层 //////////
    k=Dep[x]-Dep[y];
    for(i=;i<=s;i++)
        if(k&(<<i))x=Fa[x][i];
    if(x==y)return x;                     //x==y时，x就是最近公共祖先
    ///////////////////////////////////////////////////
    s=ceil(log(Dep[x])/log());           //计算向上倍增的上限
    for(i=s;i>=;i--)
        if(Fa[x][i]!=Fa[y][i]){ x=Fa[x][i]; y=Fa[y][i]; }
    return Fa[x][];
}

int main()
{
    int i,j,k;
    cin>>n>>m>>root;
    for(i=;i<n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add_edge(x,y);
        add_edge(y,x);//它是树，也就是无向图，所以存两次边
    }
    dfs(root,);//预处理
    for(i=;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        printf("%d\n",LCA(x,y));
    }

} 

代码（带注释）

OK吗？

这里建议去练练板子，指路-> https://www.luogu.org/problem/P3379

(哇我居然可以写蓝题了哎！！可喜可贺)

先到这里，如有问题欢迎指正

感谢观看   ありがとうございます