【HDOJ6582】Path（最短路图，最小割）

题意：

n,m<=1e4，c<=1e9

思路：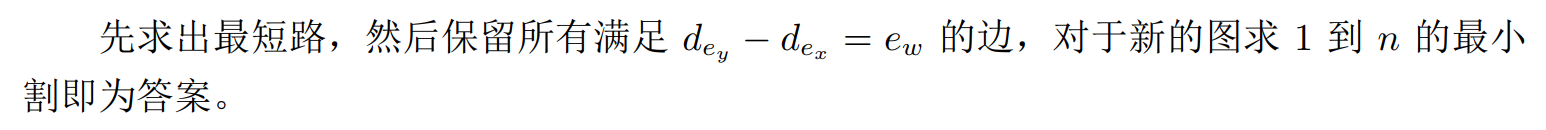

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 typedef unsigned int uint;
 typedef unsigned long long ull;
 typedef pair<int,int> PII;
 typedef pair<ll,ll> Pll;
 typedef vector<int> VI;
 #define N  110000
 #define M  1100000
 #define fi first
 #define se second
 #define MP make_pair
 #define pi acos(-1)
 #define mem(a,b) memset(a,b,sizeof(a))
 #define rep(i,a,b) for(int i=(int)a;i<=(int)b;i++)
 #define per(i,a,b) for(int i=(int)a;i>=(int)b;i--)
 #define lowbit(x) x&(-x)
 #define Rand (rand()*(1<<16)+rand())
 #define id(x) ((x)<=B?(x):m-n/(x)+1)
 #define ls p<<1
 #define rs p<<1|1

 const int MOD=1e9+;
       double eps=1e-;
       ll INF=1e14;

 priority_queue<pair<ll,int> > q;

 ll dis[N],dis1[N],dis2[N];
 int head[N],vet[N],nxt[N],len[N],vis[N],fan[N],gap[N],n,m,tot,S,T,s;

 struct arr
 {
     int x,y,z;
 }a[N];

 int read()
 {
    int v=,f=;
    char c=getchar();
    while(c<||<c) {if(c=='-') f=-; c=getchar();}
    while(<=c&&c<=) v=(v<<)+v+v+c-,c=getchar();
    return v*f;
 }

 void add(int a,int b,int c)
 {
     nxt[++tot]=head[a];
     vet[tot]=b;
     len[tot]=c;
     head[a]=tot;
 }

 void Add(int a,int b,int c)
 {
     nxt[++tot]=head[a];
     vet[tot]=b;
     len[tot]=c;
     head[a]=tot;

     nxt[++tot]=head[b];
     vet[tot]=a;
     len[tot]=;
     head[b]=tot;
 }

 void dijk(int st,int op)
 {
     mem(vis,);
     rep(i,,n) dis[i]=1e13;
     while(!q.empty()) q.pop();
     q.push(MP(,st)); dis[st]=;
     while(!q.empty())
     {
         int u=q.top().se;
         q.pop();
         if(vis[u]) continue;
         vis[u]=;
         int e=head[u];
         while(e)
         {
             int v=vet[e];
             if(dis[u]+len[e]<dis[v])
             {
                 dis[v]=dis[u]+len[e];
                 q.push(MP(-dis[v],v));
             }
             e=nxt[e];
         }
     }
     if(op==)
     {
         rep(i,,n) dis1[i]=dis[i];
     }
      else
      {
          rep(i,,n) dis2[i]=dis[i];
      }
 }

 ll dfs(int u,int aug)
 {
     if(u==T) return aug;
     int e=head[u],flow=;
     ll val=s-;
     while(e)
     {
         int v=vet[e];
         if(len[e])
         {
             if(dis[u]==dis[v]+)
             {
                 int t=dfs(v,min(len[e],aug-flow));
                 len[e]-=t;
                 len[fan[e]]+=t;
                 flow+=t;
                 if(dis[S]>=s) return flow;
                 if(aug==flow) break;
             }
             val=min(val,dis[v]);
         }
         e=nxt[e];
     }
     if(!flow)
     {
         gap[dis[u]]--;
         if(!gap[dis[u]]) dis[S]=s;
         dis[u]=val+;
         gap[dis[u]]++;
     }
     return flow;
 }

 ll maxflow()
 {
     mem(gap,);
     mem(dis,);
     gap[]=s;
     ll ans=;
     while(dis[S]<s) ans+=dfs(S,INF);
     return ans;
 }

 int main()
 {
     //freopen("1.in","r",stdin);
     //freopen("1.out","w",stdout);
     rep(i,,)
      if(i&) fan[i]=i+;
       else fan[i]=i-;
     int cas=read();
     while(cas--)
     {
         n=read(),m=read();
         rep(i,,m)
         {
             a[i].x=read();
             a[i].y=read();
             a[i].z=read();
         }
         tot=;
         rep(i,,n) head[i]=;
         rep(i,,m) add(a[i].x,a[i].y,a[i].z);
         dijk(,);
         tot=;
         rep(i,,n) head[i]=;
         rep(i,,m) add(a[i].y,a[i].x,a[i].z);
         dijk(n,);
         tot=;
         rep(i,,n) head[i]=;
         rep(i,,m)
          if(dis1[a[i].x]+a[i].z+dis2[a[i].y]==dis1[n])
           Add(a[i].x,a[i].y,a[i].z);

         S=; T=n; s=n;
         ll ans=maxflow();
         printf("%I64d\n",ans);
     }
     return ;
 }