清北学堂2019.7.18 & 清北学堂2019.7.19

Day 6 钟皓曦

经典题目：石子合并

可以合并任意两堆，代价为数量的异或（^）和

f[s]把s的二进制所对应石子合并成一堆所花代价

枚举s的子集

#include<iostream>

using namespace std;

int main()
{
    cin >> n;
    for (int a=;a<n;a++)
        cin >> z[a];
    for (int a=;a<(<<n);a++)
        for (int b=;b<n;b++)
            if (a & (<<b))
                sum[a] += z[b];

    memset(f,0x3f,sizeof(f));
    for (int a=;a<n;a++)
        f[<<a] = ;

    for (int s=;s<(<<n);s++)
        for (int a=;a<s;a++)
            if ( (s|a) == s)
                f[s] = min(f[s],f[a]+f[a^s]+(sum[a]^sum[a^s]));

    for (int s=;s<(<<n);s++)
        for (int a=(s-)&s;a;a=(a-)&s)
            f[s] = min(f[s],f[a]+f[a^s]+(sum[a]^sum[a^s]));

    cout << f[(<<n)-] << endl;

}

然后今天的正题就是博弈论dp了【nim游戏：据说80%的博弈论dp最终都会转化到nim游戏上来】

其实这种题型只与Alice和Bob有关（大雾

这种东西大概是这样的

有一个游戏g，有两个人Alice和Bob在Van它，是回合制游戏，该游戏无平局，胜负条件：当某个人无法操作时就输了

下面以好多好多的题来说明

T1

有一个整数S（2<=S<=200），先手在S上减掉一个数x，至少是1，但小于S。之后双方轮流把S减掉一个正整数，但都不能超过先前一回合对方减掉的数的k倍，减到0的一方获胜。问先手是否必胜？

solution：

从一个状态转到另外一种状态，会有必败态和必胜态出现

f[s]   s->false 必报 s->true 必胜

状态由s->s1.s2.s3······

若对于任意的f[si]=true则走向了必胜态。

直接记忆化搜索！

dp[i][j]表示当前剩下的数为i，最多能减的数为j的状态，dp[i][j] = = 1必胜，否则必败

dp[i][j]->dp[i-x][x*k](1<=x<=j)

如果对于某个x， dp[i-x][x*k] = = 0，则dp[i][j]=1,否则dp[i][j]=0

要求的为dp[S][S-1]

O(S^3)

f[i][j]还剩下i，对手上一轮减的数字是j，此时自己是必胜态还是必败态【伪代码】

#include<iostream>

using namespace std;

bool f[][],g[][];

bool dfs(int i,int j)
{
    if (i==) return false;
    if (g[i][j]) return f[i][j];
    g[i][j]=true;f[i][j]=false;
    for (int r=;r<=i && r<=k*j;r++)
        if (dfs(i-r,r) == false) f[i][j]=true;
    return f[i][j];
}

int main()
{
    cin >> s >> k;
    for (int a=;a<s;a++)
        if (dfs(s-a,a) == false)
        {
            cout << "Alice" << endl;
            return ;
        }
    cout << "Bob" << endl;

    return ;
}

T2

若现在有n个游戏

定义sg函数：能转移到的状态中sg函数里没有出现的最小的自然数

sg[0]=0

sg定理：

n个游戏的sg值=每个sg值异或起来

T3

若现在一次只能取走1-4个石子

同样的操作：sg[0]=0 sg[1]=1 sg[2]=2 sg[3]=3 sg[4]=4 sg[5]=0

T4

n+1堆石子，最左边一堆石头有2012个，两个人分别进行操作。一次操作可以选取两堆不同的石堆分别增加或减少一个石子（一加一减，或给已经不剩石子的堆加一个都是允许的）。为了保证游戏会在有限步内结束，规定所选的两堆中右边的那一堆一定要包含奇数个石子,无路可走者输.问先手是否必胜？

计算n堆的奇偶性，把所有奇数石子堆的下标取出来异或，看答案是否为0

有两堆一样的石子与没有事一个概念

通过转化奇数堆的石子，来解决问题

将最左边一堆视为第0堆，将石子数为奇数的石子堆的编号异或起来，结果为0则先手必败，否则必胜

其实是转化为了nim博弈

T5

u  有N堆石子放在N级楼梯上，楼梯编号为0..N-1，每堆有a[n]个石子。两人轮流游戏，每次将任意堆中的任意个石子移动到它下面那一层楼梯上,0号的石子不能动。直到所有石子都移动到0号,那个人就赢了。问先手是否有必胜策略 。

将距离终点步数为奇数的格子棋子数量异或起来就是答案

T6

u1xN(1<=N<=2000)的空格子，双方轮流操作，每次选一个没有被标记的格子，将其标记，如果某人操作完后，存在3个连续的格子都被标记了，那么他就获胜了，问先手是否有必胜策略？

把一个游戏看成多个游戏

再分成多个游戏

sg[i],对于一个长度为i的横条的sg值为多少

防止越界：在数组后面加一个足够大的数就行

#include<iostream>
#include<algorithm>
#include<vector>

using namespace std;

int dfs(int n)
{
    if (n==) return ;
    if (f[n]) return sg[n];
    f[n]=true;
    vector<int> z;
    for (int a=;a<=n;a++)
    {
        int l = max(a-,);
        int r = max(n-a-,);
        z.push_back( dfs(l) ^ dfs(r) );
    }
    sort(z.begin(),z.end());
    z.push_back();

    for (int a=,p=;;a++)
    {
        if (z[p] != a)
        {
            sg[n] = a;
            return sg[n];
        }
        while (z[p]==a)
            p++;
    }
}

int main()
{
    cin >> n;
    if (dfs(n)) cout << "Alice" << endl;
    else cout << "Bob" << endl;
}

留一个练习：

bzoj2798

Day 7 钟皓曦

消防局的设立

不用dp的做法

N<=100000

f[i][0/1][k]

在自己，父亲，兄弟，爷爷结点都能将其覆盖

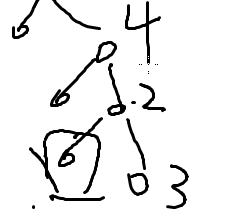
（显然放4结点最优）

首先对于这棵树，找出深度最深的结点，找到其爷爷，在爷爷结点放一个士兵，把他爷爷能覆盖到的结点删掉，以此类推，对剩下的树进行类似操作，直至树全被覆盖

用堆维护，时间复杂度O（n log n）

求出n的k个因子

再计算m^k即可

若将人进行编号，求不同分组呢？

每组有 n/r 个人，则方案数为

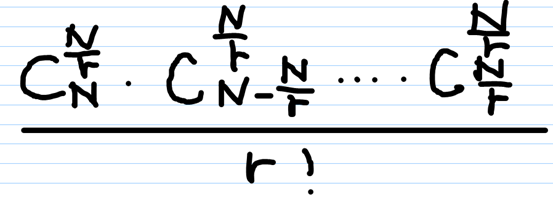
这么多种情况，然后化简

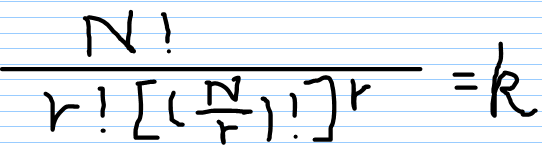
用过欧拉定理后转化为计算

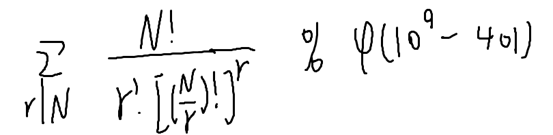
1e9-401是个质数，而1e9-402=2*13*5281*7283

让n的阶乘%2 13 5281 7283

再合并

因为%数较小，一定会有循环节出现

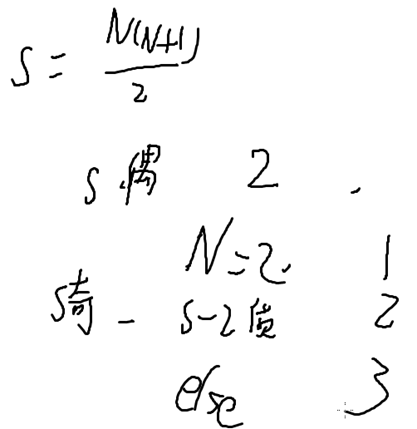
f[i][j]表示走了i步，走到了j

N个点的数，有点权

有m次询问，每次给两个点p1,p2，在这条路径上能否找出三个点，使得它们可以形成三角形

m,n<=1e6

斐波那契数列

若两点的距离大于42，输出yes

若小于等于，暴力即可

bzoj 树上三角形