洛谷P4095新背包问题

传送

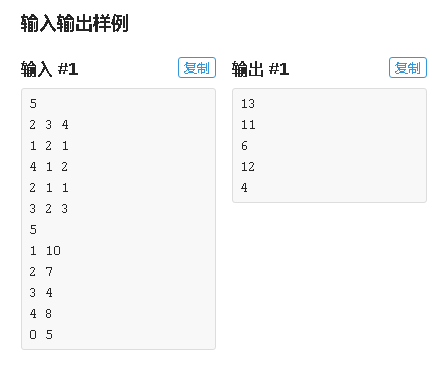
这道题最最暴力的方法就是对于每一个询问都跑一边多重背包问题，但显然q不会那么友好的让我们用暴力过掉这道题。

考虑优化。我们可以先把裸的多重背包搞成二进制优化后的多重背包。但是复杂度依然无法接受。接下来使用吸氧和register等玄学优化 然而你发现你还是T了

那我们可不可以记录下来第i种不选，总容量为j($1\leq j\leq 1000$时的最大价值？想法很好，但是暴力写出来复杂度还是太高(O(\(1000n^2logn\)))

暴力写出来的

for(int i=1;i=st[i]&&k=w[k];j--)
    f[i][j]=max(f[i][j],f[i][j-w[k]]+v[k]);
  }
}
    

上面的程序复杂度主要高在什么地方呢？f[i][j]和f[i-1][j]相比，考虑的物品多了第i-1种物品，少了第i种物品，而其他不变。但是上面的程序枚举哪一种物品不选后就全部重新考虑了一遍，会造成很大的浪费。

为了减少浪费，我们可以把上面的f[i][j]拆成两部分。可以先算出选1_{i-1种物品最大价值，再算出选i+1}n种物品的最大价值，枚举合并的价值即可。

Code:

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<cmath>
using namespace std;
const int inf=214748364;
typedef long long ll;
inline int read()
{
	char ch=getchar();
	int x=0;bool f=0;
	while(ch<'0'||ch>'9')
	{
		if(ch=='-')f=1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
    {
    	x=(x<<3)+(x<<1)+(ch^48);
    	ch=getchar();
    }
    return f?-x:x;
}
int n,w[10009],v[10009],q,t;
int st[1009],en[1009],me,meyo[300009],m[300009],dp[2009][1009],f[1009][1009],g[1009][1009];
bool have[1009][1009],ha[1009];
void Dp()
{
	for(register int duliu=1;duliu<=n;duliu++)
	{
	    for(int j=1;j<=1000;j++)
	     f[duliu][j]=f[duliu-1][j];
	    for(int i=st[duliu-1];i<=en[duliu-1];i++)
		 for(int j=1000;j>=w[i];j--)
		  f[duliu][j]=max(f[duliu][j],f[duliu][j-w[i]]+v[i]);
	}
	for(int duliu=n;duliu>=1;duliu--)
	{
		for(int j=1;j<=1000;j++)
		 g[duliu][j]=g[duliu+1][j];
		for(int i=st[duliu+1];i<=en[duliu+1];i++)
		 for(int j=1000;j>=w[i];j--)
		  g[duliu][j]=max(g[duliu][j],g[duliu][j-w[i]]+v[i]);
	}
}
int main()
{
	memset(st,0x3f,sizeof(st));
	n=read();
	for(register int i=1;i<=n;i++)
	 {
	 	int mo=read(),va=read(),num=read();
	 	int k=1;
	 	st[i]=t+1;
	 	while(num>=k)
	 	{
	 		w[++t]=mo*k;
	 		v[t]=va*k;
	 		num-=k;
			k*=2;
	 	}
	 	if(num)
	 	{
	 		w[++t]=mo*num;
	 		v[t]=va*num;
	 	}
	 	en[i]=t;
	 }
	q=read();
	for(register int i=1;i<=q;i++)
      meyo[i]=read()+1,m[i]=read(),have[meyo[i]][m[i]]=1,ha[meyo[i]]=1;
    Dp();
	for(register int i=1;i<=q;i++)
    {
    	int ans=0;
    	for(int j=0;j<=m[i];j++)
    	 ans=max(ans,f[meyo[i]][j]+g[meyo[i]][m[i]-j]);
    	printf("%d\n",ans);
    }
}

然鹅这题正解是cdq分治，but我不会

maybe窝搞完单调队列优化之后会回来写cdq分治的

希望上面那条不要变成最小鸽