D3(没写完

说在博客前

这篇博客有许多使用到 STL 的地方，由于本人实在是记不全，所以我也参考了北大的一些教材，就别说我黈力了 QwQ

数据结构

今天讲的是数据结构啦（也是我这个蒟蒻最喜欢的

一些天天见面的好盆友

栈，队列

这些吧都是些挺水的东西，我就口胡口胡。（结果口胡着口胡着过万了？？？？？？)

值得一提的是 队列常用于 bfs，栈一般就是用于中序和后序遍历

堆

堆是一种很有意思的数据结构

它允许元素的堆顶弹出，堆低插入，而 c++ 当中的 stl 提供了 priority_queue（优先队列）这个容器，允许你对于这个队列采用特定的方式优先排序

对于一个堆，我们一般只说大根堆和小根堆，c++ 默认是大根堆，想要实现小根堆，我们可以这样

priority_queue<int, vector<int>, greater<int> >;//注意此处 > 要用空格空开，有可能识别为右移

倍增求 LCA

我们有一棵树，定义一棵树上的点到根结点的路径上所有的点都是它的祖先，LCA 指的就是两个数的最近公共祖先

步骤大体是这样

1. 如果 A 的深度小于 B 的深度，就把他们互换

2. 把 a 向上调到和 b 一样的高度，直到 ab 一样高（此时 ab 可以进行互换）

3. 把 a 和 b 一起上调，直到 ab 相同

这种算法复杂度是 O(deep) 的，但是当树是一条类似于链的结构，就废了，考虑为什么？

我们是一层一层跳的，自然会很慢，所以我们可以考虑倍增着来求 LCA

令

p [x] [i]

表示 x 向后 2^i 的祖先是谁，显然 p[x] [i] = p[ p [x] [i - 1] ] [i - 1]

用这张图举例，我们想要求出 4，5 的 LCA

就要

1. 先 dfs 所有点，处理出每一个点的深度

2. 然后把深度更深的那一个点（4）一个点地一个点地往上跳，直到到某个点（3）和另外那个点（5）的深度一样

然后两个点一起一个点地一个点地往上跳，直到到某个点（就是最近公共祖先）两个点“变”成了一个点

不过有没有发现一个点地一个点地跳很浪费时间？

如果一下子跳到目标点内存又可能不支持，相对来说倍增的性价比算是很高的

　　倍增的话就是一次跳 2^i 个点，不难发现深度差为 x 时，深度更深的那个点就需要跳 x 个点

所以代码就是这个样子

if (depth[a] < depth[b])
    swap(a, b);
int c = depth[a] - depth[b];
for (int i = 0; i <= 20; i++)
{
    if (c & (1 << i))
    {
        a = up[a][i];
    }
}

这样子看起来很不错对吧，但是会出现一个问题，那就是跳到的公共祖先不一定是最近的

所以倍增找 LCA 的方法是这样的

在两个人平了之后，从最大可以跳的步数开始跳（一定是 2^i)，

（这就是为什么我们说求 LCA 的过程很像二进制分解的原因了）

如果跳的到的位置一样，就不跳，如果不一样才跳，每次跳的路程是前一次的一半

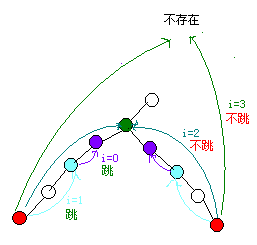
这样做有一个缺点，就是它找到的点是最靠近 LCA 的点，也就是再跳一步就是 LCA，不过问题不大

在上代码之前，说几句

我个人是比较喜欢预处理和dfs写在一起的，然后fa[i] 我也直接用fji代替了，所以省了一点点空间吧

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>

using namespace std;

const int Maxn = 500005, Maxc = 20;
int n, x, y, s, m;
int head[Maxn], edge_num = 0;
struct EDGE
{
    int next, to;
} e[Maxn * 2];
int dep[Maxn];
bool visited[Maxn];
int fa[Maxn][21];

inline void add(int from, int to)
{
    e[++edge_num].next = head[from];
    e[edge_num].to = to;
    head[from] = edge_num;
}
void dfs(int u, int father)
{
    dep[u] = dep[father] + 1;
    fa[u][0] = father;
    for (int i = 0; i <= Maxc - 1; ++i)
        fa[u][i + 1] = fa[fa[u][i]][i];
    for (int i = head[u]; i; i = e[i].next)
    {
        int v = e[i].to;
        if (v != father)
            dfs(v, u);
    }
}

inline int LCA(int x, int y)
{
    if (dep[x] < dep[y])
        swap(x, y); //让A在下面
    for (int i = Maxc; i >= 0; --i)
    {
        if (dep[fa[x][i]] >= dep[y])
            x = fa[x][i];
        if (x == y)
            return x;
    }
    for (int i = Maxc; i >= 0; --i)
        if (fa[x][i] != fa[y][i])
            x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}

int main()
{
    scanf("%d%d%d", &n, &m, &s);
    for (int i = 1; i <= n - 1; ++i)
    {
        scanf("%d%d", &x, &y);
        add(x, y);
        add(y, x);
    }
    dfs(s, 0);
    while (m--)
    {
        scanf("%d%d", &x, &y);
        printf("%d\n", LCA(x, y));
    }
}

不想写了md