luoguP1288 取数游戏II [博弈论]

题目描述

有一个取数的游戏。初始时，给出一个环，环上的每条边上都有一个非负整数。这些整数中至少有一个0。然后，将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏，两人轮流取数，取数的规则如下：

（1）选择硬币左边或者右边的一条边，并且边上的数非0；

（2）将这条边上的数减至任意一个非负整数(至少要有所减小)；

（3）将硬币移至边的另一端。

如果轮到一个玩家走，这时硬币左右两边的边上的数值都是0，那么这个玩家就输了。

如下图，描述的是Alice和Bob两人的对弈过程，其中黑色节点表示硬币所在节点。结果图(d)中，轮到Bob走时，硬币两边的边上都是0，所以Alcie获胜。

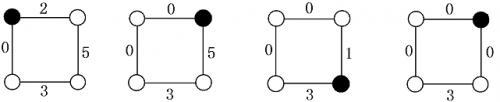
（a）Alice （b）Bob （c）Alice （d）Bob

现在，你的任务就是根据给出的环、边上的数值以及起点（硬币所在位置），判断先走方是否有必胜的策略。

输入输出格式

输入格式：

第一行一个整数N（N≤20），表示环上的节点数。

第二行N个数，数值不超过30，依次表示N条边上的数值。硬币的起始位置在第一条边与最后一条边之间的节点上。

输出格式：

仅一行。若存在必胜策略，则输出“YES”，否则输出“NO”。

输入输出样例

输入样例#1：

【输入1】
4
2 5 3 0
【输入2】
3
0 0 0

输出样例#1：

【输出1】
YES
【输出2】
NO

---

无限手膜，手膜而死。
不过正确性还是够用的。

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;

 const int maxn=;

 int n;
 int a[maxn];

 int main(){
     scanf("%d",&n);
     for(int i=;i<=n;i++)  scanf("%d",&a[i]);
     for(int i=;i<=n;i++)
         if(!a[i])
             if(!(i&)){
                 puts("YES");
                 return ;
             }
             else  break;
     for(int i=n;i;i--)
         if(!a[i])
             if((n-i)&){
                 puts("YES");
                 return ;
             }
             else  break;
     puts("NO");
     return ;
 }

__stdcall的博弈搜索好强啊

参(chao)考(xi)一下他的solution

首先尝试无脑的博弈搜索，60分

然后开始想优化。。。

对于状态0*0，*表示当前处在的位置，是我们知道的第一个必败状态

那么对于状态0*n 0，就是必胜状态，对称的时候同理

然后0*1 n 0就是必败状态，因为只能转移到0*n 0

我们还知道0 n*m 0是必胜状态

所以0*n m 0就是必败状态，因为只能转移到0*n 0（必胜）和0 a*b 0（必胜）

于是0*a b c 0就是必胜状态，0 a*b c 0是必胜状态

所以0*a b c d 0是必败状态

由以上可得知，对于0*a b c d e...0的状态，如果两个0中间的长度为偶数，必败，长度为奇数，必胜

然后对于任意的0 a*...和...*a 0的状态，必胜

然而还是TLE三个点啊。。。继续分析吧

好像有一个很简单的优化，根据上面的分析得知

如果当前状态是0 a b...*...c d 0

这时候可以选择把左边相邻状态变为0或者把右边相邻的变为0

如果这两种有一个必败状态，则此状态必胜

过了。。。大成功。

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #include <cstring>
 #include <vector>
 using namespace std;
 int n;
 int a[];
 int next( int idx ) {
     if( idx == n- ) return ;
     else return idx+;
 }
 int prior( int idx ) {
     if( idx ==  ) return n-;
     else return idx-;
 }
 bool dfs( int idx ) {
     if( a[idx] ==  && a[prior(idx)] ==  ) return false;
     if( a[idx] !=  && a[next(idx)] ==  ) return true;
     if( a[prior(idx)] !=  && a[prior(prior(idx))] ==  ) return true;
     if( a[idx] ==  ) { // 确定状态，右边为0
         int cnt = ;
         for( int i = prior(idx) ; a[i] !=  ; i = prior(i) ) ++cnt;
         if( (cnt&) ) return true;
         else return false;
     }
     if( a[prior(idx)] ==  ) {
         int cnt = ;
         for( int i = idx ; a[i] !=  ; i = next(i) ) ++cnt;
         if( (cnt&) ) return true;
         else return false;
     }
     // 把右边变为0
     int tmp = a[idx]; a[idx] = ;
     if( dfs(next(idx)) == false ) {
         a[idx] = tmp;
         return true;
     }
     a[idx] = tmp;
     // 把左边变为0
     tmp = a[prior(idx)]; a[prior(idx)] = ;
     if( dfs(prior(idx)) == false ) {
         a[prior(idx)] = tmp;
         return true;
     }
     a[prior(idx)] = tmp;
     // 其他的各种尝试
     for( int i =  ; i < a[idx] ; ++i ) {
         a[idx] -= i;
         if( dfs(next(idx)) == false ) {
             a[idx] += i;
             return true;
         }
         a[idx] += i;
     }
     for( int i =  ; i < a[prior(idx)] ; ++i ) {
         a[prior(idx)] -= i;
         if( dfs(prior(idx)) == false ) {
             a[prior(idx)] += i;
             return true;
         }
         a[prior(idx)] += i;
     }
     return false;
 }
 int main() {
     scanf( "%d" , &n );
     for( int i =  ; i < n ; ++i ) scanf( "%d" , &a[i] );
     if( dfs() ) printf( "YES\n" );
     else printf( "NO\n" );
     return ;
 }