导数、多元函数、梯度、链式法则及 BP 神经网络

一元函数的导数

对于函数\(y=f(x)\)，导数可记做\(f'(x_0)\)、\(y'|x=x_0\)或\(\frac{dy}{dx}|x=x_0 \)。定义如下：
\[f'(x_0) = \lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0}\frac{f(x_0+\Delta x) - f(x)}{\Delta x}\]
一阶导数也是一个函数，这个函数的导数称为二阶导数，可以依此递归定义。
\[f^{(n)}(x) = [f^{(n-1)}(x)]'\]

多元函数及其偏导数

一般的，假设 \(f\) 是\(\mathbb{R}^n\)到\(\mathbb{R}\)的映射，记做 \(y = f(\boldsymbol{x})\)，其中 \(\boldsymbol{x}\) 是 \(n\) 维向量。若 \(n \geqslant 2\)，则称 \(f\) 是多元函数。一个简单的例子是\(z=x^2+y^2 + 2xy\)。
以二阶导数\(z=f(x,y)\)为例，说明偏导数的概念。
如果
\[\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x,y_0) - f(x_0,y_0)}{\Delta x}\]
存在，则称此极限为函数在点 \((x_0,y_0)\) 处对 \(x\) 的偏导数，记做\(\frac{\partial f}{\partial x}|_{x=x_0,y=y_0}\)。
偏导数也是自变量 \(x,y\) 的函数，称为偏导函数，记做\(\frac{\partial f}{\partial x}\)，也是一个二元函数。
类似高阶导数，也有高阶偏导数，由于变量比较多，导致形式比较复杂。比如二阶函数的二阶偏导数就有四种：
\[\frac{\partial}{\partial x}(\frac{\partial f}{\partial x}) = \frac{\partial^{2} f}{\partial x^2}\]
\[\frac{\partial}{\partial y}(\frac{\partial f}{\partial x}) = \frac{\partial^{2} f}{\partial x \partial y}\]
\[\frac{\partial}{\partial x}(\frac{\partial f}{\partial y}) = \frac{\partial^{2} f}{\partial y \partial x}\]
\[\frac{\partial}{\partial y}(\frac{\partial f}{\partial y}) = \frac{\partial^{2} f}{\partial y^2}\]

其中第二、三项称为混合偏导数。对于二元函数来说，两个混合偏导数是相等的。

复合函数及链式法则

从一元函数出发，设 \(x\) 是实数，\(f\) 和 \(g\) 是从实数映射到实数的函数。假设 \(y = g(x)\)，且 \(z = f(g(x)) = f(y)\)，即 \(z\) 是 \(x\) 的符合函数。链式法则是指
\[\frac{dz}{dx} = \frac{dz}{dy}\frac{dy}{dx}\]
可以通过泰勒展开式来证明。下面是通过链式法则计算导数的一个例子。

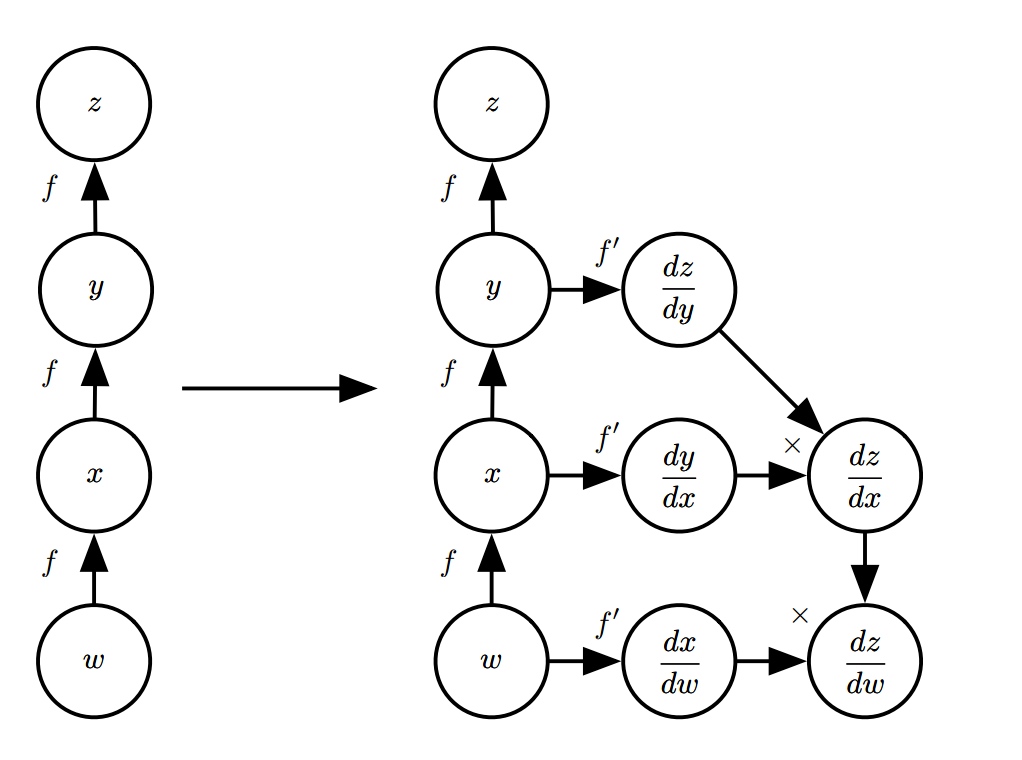
从标量可以推广到向量。假设 \(\boldsymbol{x} \in \mathbb{R}^m, \boldsymbol{y} \in \mathbb{R}^n\)，\(g\) 是从 \(\mathbb{R}^m\) 到 \(\mathbb{R}^n\) 的映射， \(f\) 是从 \(\mathbb{R}^n\) 到\(\mathbb{R}\) 的映射。假设 \(\boldsymbol{y} = f(\boldsymbol{x})\)并且 \(z = f(\boldsymbol{y})\)，则
\[\frac{\partial z}{\partial x_i} = \sum_{j}\frac{\partial z}{\partial y_j}\frac{\partial y_j}{\partial x_i} \]
用向量表示，即
\[\nabla_{\boldsymbol{x}}z = (\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}})^T\nabla_{\boldsymbol{y}}z \]
也可以用多元函数的泰勒展开来证明。其中 \(\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}}\) 是雅克比矩阵
\[\begin{bmatrix}\frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_m}\\
\frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_m}\\
\vdots & \vdots & \ddots &\vdots\\
\frac{\partial y_n}{\partial x_1} & \frac{\partial y_n}{\partial x_2} & \cdots & \frac{\partial y_n}{\partial x_m}\end{bmatrix}\]
特别的，如果 \(\boldsymbol{y} = \boldsymbol{Wx}\)，则 \(\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} = \boldsymbol{W}\)
\(\nabla\) 是哈密顿算子，对于二元函数，\(\nabla = \frac{\partial}{\partial x}\vec{i}+\frac{\partial}{\partial y}\vec{j}\) 。
推广到多元函数，可以得到
\[\nabla_{\boldsymbol{x}} = (\frac{\partial}{\partial x_1},\frac{\partial}{\partial x_1},\cdots ,\frac{\partial}{\partial x_n})^T\]
那么
\[\nabla_{\boldsymbol{x}}z = (\frac{\partial z}{\partial x_1},\frac{\partial z}{\partial x_1},\cdots ,\frac{\partial z}{\partial x_n})^T\]
是一个 \(n\) 维列向量。同理 \(\nabla_{\boldsymbol{y}} z\) 是一个 \(m\) 维列向量。

梯度及梯度下降法

一元函数的情况

还是从一元函数入手，设 \(y = f(x)\)，我们要找一个\(x^*\)，使得 \( f(x^*)\)是函数的极小值。
如果有一个序列\(x^0,x^1,x^2,\cdots\)，满足\(f(x^{t+1})<f(t)\)，那么不断执行这一过程，可能会收敛到局部极小点。
那么问题就是如何构造这么一个序列。根据泰勒展示，有
\[f(x+\Delta x) \simeq f(x) + \Delta x f'(x)\]
那么取\(\Delta x = -\gamma f'(x)\)，即变化量和导数的符号相反。其中步长 \(\gamma\) 是一个小常数，这是因为上面的泰勒展开式的高阶项只有在比较小的邻域才可以忽略。“步子太大容易扯着蛋”。
那么，小常数究竟有多小呢？根据数学知识可以证明，若函数满足 L-Lipschitz 条件，把步长设置为 \(1/(2L)\) 即可确保收敛到局部极值点。

多元函数

对于多元函数 \(y = f(\boldsymbol{x})\)，我们也想通过类似的方法来求得极小值点 \(\boldsymbol{x^*}\)。
\(n\) 维空间中两个点的差值是一个向量，方向可能有无数多个。如果要尽快收敛到极小值点，那么应该沿着函数值下降最快的方向前进。
假设沿着方向\(\boldsymbol{l}\) 前进，\(\boldsymbol{l}\) 的单位向量\(\boldsymbol{l_0}\)在各个方向的投影分别是\((cos\alpha_1,cos\alpha_2,\cdots,cos\alpha_n)\)，那么从\(\boldsymbol{x_0}\)沿着方向\(\boldsymbol{l}\) 前进 \(t\) 的值记为 \(g(t)= f(\boldsymbol{x_0} + \boldsymbol{l_0}t)\)，那么根据链式法则， \(g(t)\) 在 \(t=0\) 的导数，即函数\(f(\boldsymbol{x})\) 在方向 \(\boldsymbol{l}\) 上的方向导数为
\[(\frac{\partial f}{\partial \boldsymbol{x}}|\boldsymbol{x=x_0})^T(\frac{\partial \boldsymbol{x_0} + \boldsymbol{l_0}t}{\partial t}) = \nabla_{\boldsymbol{x}} f \centerdot \boldsymbol{l_0}\]

显然\(\boldsymbol{l_0}\) 和 \(\nabla_{\boldsymbol{x}} f\) 方向一致时，方向导数最大。这个方向即是函数的梯度方向，函数沿着这个方向的变化最快，变化率最大。
而我们的目标是沿着函数值下降最快的方向前进，即应该沿着负梯度的方向前进，即取
\[\Delta \boldsymbol{x} = - \gamma \nabla f(\boldsymbol{x})\]
只要 \(\gamma\) 足够小，且函数满足 L-Lipschitz 条件，这样子选取一系列的点一定可以收敛到局部极小点。这个方法被称为梯度下降法。

神经网络及BP算法

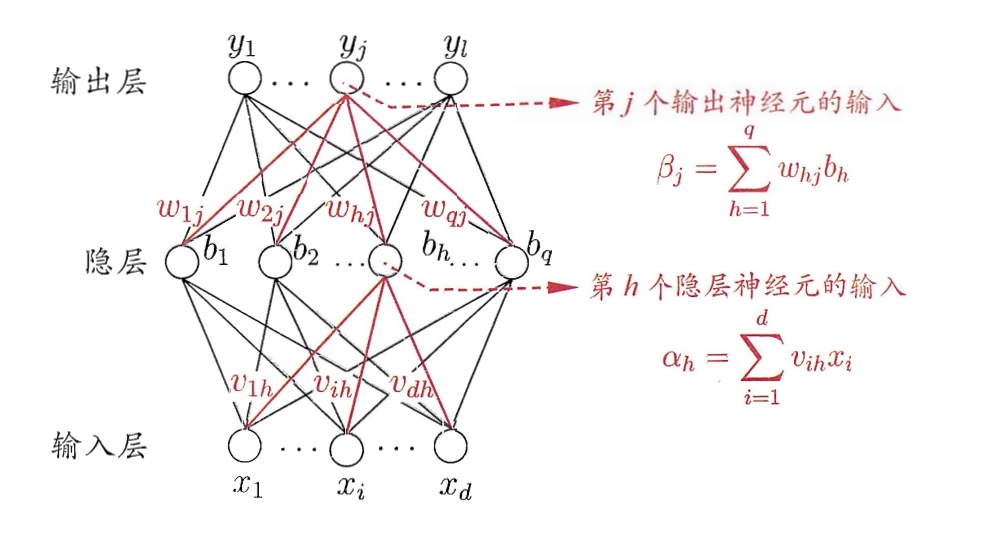
上面是一个神经网络的例子，输入节点有 \(d\) 个，输出节点有 \(l\) 个，隐藏节点有 \(q\)个。输出层第 \(j\) 个节点的阈值用 \(\theta _j\) 表示，隐层的第 \(h\) 个神经元用 \(\gamma _h\)表示。
从输入 \(\boldsymbol{x}\) 到输出 \(\boldsymbol{y}\) 的过程如下。

获取隐层的输入：
\[\boldsymbol{\alpha}=\boldsymbol{Vx}\]
其中\(\boldsymbol{V}\) 是 \(q\times d\) 的矩阵，\(\boldsymbol{\alpha}\) 是 \(q\) 维向量。
获取隐层的输出：
\[\boldsymbol{b} = f(\boldsymbol{\alpha + \gamma})\]
获取输出层的输入：
\[\boldsymbol{\beta } = \boldsymbol{Wh}\]
其中\(\boldsymbol{W}\) 是 \(l\times q\) 的矩阵。
获取输出层的输出：
\[\boldsymbol{y} = f(\boldsymbol{\beta + \theta})\]

综合起来，可以认为是
\[\boldsymbol{y} = \boldsymbol{F(x,V,\gamma,W,\theta)}\]
我们的目标是确定\(\boldsymbol{V, \gamma, W, \theta}\)，使得下面式子最小
\[\boldsymbol{J(V,\gamma,W,\theta)}=\sum_{\boldsymbol{x}\in\mathbb{X}}(\boldsymbol{y}^* - \boldsymbol{F(x,V,\gamma,W,\theta)})^2\]
其中 \(\mathbb{X}\)是训练集数据，\(\boldsymbol{y}^*\) 是标注。
我们尝试使用梯度下降法来得到一个极小值点，那么需要求得函数 \(\boldsymbol{J}\) 对与 \(\boldsymbol{V, \gamma, W, \theta}\) 的梯度。只需获得函数 \(\boldsymbol{F}\)，即网络的输出\(\boldsymbol{y}\) 对应的梯度即可。

首先，求关于\(\boldsymbol{\theta}\) 的梯度。
根据链式法则，
\[\frac{\partial F}{\partial \boldsymbol{\theta}} = (\frac{\partial (\boldsymbol{\theta + \beta})}{\partial \boldsymbol{\theta}})^T\frac{\partial F}{\partial (\boldsymbol{\theta + \beta})} = \frac{\partial F}{\partial (\boldsymbol{\theta + \beta})}\]
求关于\(\boldsymbol{W}\) 的梯度

\[\frac{\partial F}{\partial \boldsymbol{W}} = (\frac{\partial \boldsymbol{ \beta}}{\partial \boldsymbol{W}})^T\frac{\partial F}{\partial \boldsymbol{ \beta}}\]
其中 \[\frac{\partial \boldsymbol{ \beta}}{\partial \boldsymbol{W}} = \begin{bmatrix}\frac{\partial \boldsymbol{ \beta}}{\partial w_{11}} & \frac{\partial \boldsymbol{ \beta}}{\partial w_{21}} &\cdots &\frac{\partial \boldsymbol{ \beta}}{\partial w_{l1}}\\
\frac{\partial \boldsymbol{ \beta}}{\partial w_{12}} & \frac{\partial \boldsymbol{ \beta}}{\partial w_{22}} &\cdots &\frac{\partial \boldsymbol{ \beta}}{\partial w_{l2}}\\
\vdots & \vdots & \ddots & \vdots\\
\frac{\partial \boldsymbol{ \beta}}{\partial w_{1q}} & \frac{\partial \boldsymbol{ \beta}}{\partial w_{2q}} &\cdots &\frac{\partial \boldsymbol{ \beta}}{\partial w_{lq}}\end{bmatrix}\]
每一个元素都是一个向量。带入得到
\[\frac{\partial F}{\partial w_{ij}} = (\frac{\partial \boldsymbol{\beta}}{\partial w_{ij}})^{T} (\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{\beta}})\]
\(\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{\beta}}\)可类似\(\frac{\partial F}{\partial \boldsymbol{\theta}}\) 求出
求关于 \(\boldsymbol{\gamma}\) 的梯度

\[\frac{\partial F}{\partial \boldsymbol{\gamma}} = (\frac{\partial \boldsymbol{b}}{\partial \boldsymbol{\gamma}})^T(\frac{\partial F}{\partial \boldsymbol{b}})\]
其中\(\frac{\partial \boldsymbol{b}}{\partial \boldsymbol{\gamma}}\)可以很容易求出。
\[\frac{\partial F}{\partial \boldsymbol{b}} = (\frac{\partial \boldsymbol{\beta}}{\partial \boldsymbol{b}})^T(\frac{\partial F}{\partial \boldsymbol{\beta}})\\ \frac{\partial \boldsymbol{\beta}}{\partial \boldsymbol{b}} = \boldsymbol{W}\]
求关于 \(\boldsymbol{V}\)的梯度

\[\frac{\partial F}{\partial \boldsymbol{V}} = (\frac{\partial \boldsymbol{ \alpha}}{\partial \boldsymbol{V}})^T\frac{\partial F}{\partial \boldsymbol{ \alpha}}\]
同样根据链式法则，有
\[\frac{\partial F}{\partial \boldsymbol{ \alpha}} = (\frac{\partial \boldsymbol{b}}{\partial \boldsymbol{\alpha}})^T(\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{b}})\]

如果有更多的隐含层，可以继续通过链式法则来求得每一层的梯度，然后根据梯度下降法来求得极小值点。如果网络的结构比较复杂，比如 RNN，同样可以通过链式法则求得关于参数的梯度，不过需要更多的 trick。
值得注意的是，反向传播，或者说 BP 算法，只是计算梯度的方法。求得梯度以后，可以有很多种方法来求极小值，比如随机梯度下降。

参考

Matrix calculus
周志华. 机器学习[M]. 清华大学出版社, 2016.
Goodfellow I, Bengio Y, Courville A. Deep Learning[M]. The MIT Press, 2016.