混沌数学之拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)
拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)是
1979年苏联物理学家拉比诺维奇和法布里康特提出模拟非平衡介
质自激波动的非线性常微分方程组:
dot{x} = y (z - 1 + x^2) + \gamma x
dot{y} = x (3z + 1 - x^2) + \gamma y
dot{z} = -2z (\alpha + xy)
其中 α, γ 是控制系统的参数.
Danca and Chen指出由于拉比诺维奇-法布里康特方程包含平方项,
因此比较难以分析,即便选择的参数相同,但由于求解微分方程
组的步骤的不同也会导致不同的吸引子。
参数值:α=1.1,γ=0.803..0.917,t=0...130
初始条件:x(0)=-1,y(0)=0,z(0)=0.5
在t<20时,系统表现为自激振动,当t>20,系统进入馄饨态。
相关软件:混沌数学及其软件模拟
相关代码:
class RabinovichFabrikantEquation : public DifferentialEquation
{
public:
RabinovichFabrikantEquation()
{
m_StartX = -1.0f;
m_StartY = 0.0f;
m_StartZ = 0.5f; m_ParamA = 1.1f;
m_ParamB = 0.87f; m_StepT = 0.002f;
} void Derivative(float x, float y, float z, float& dX, float& dY, float& dZ)
{
dX = y*(z - + x*x) + m_ParamB*x;
dY = x*(*z + - x*x) + m_ParamB*y;
dZ = -*z*(m_ParamA + x*y);
} bool IsValidParamA() const {return true;}
bool IsValidParamB() const {return true;}
};
相关截图:


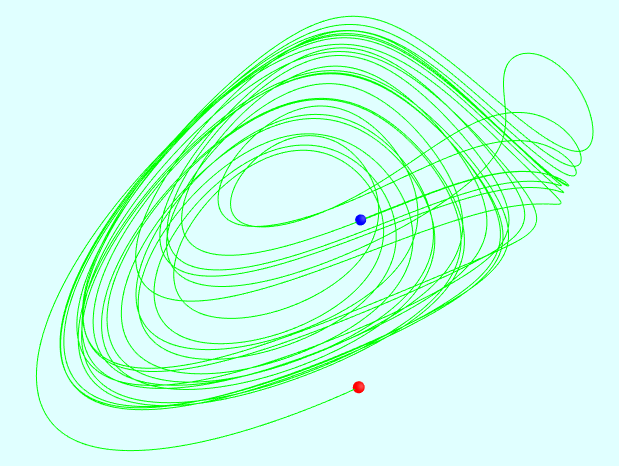

混沌数学之拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)的更多相关文章
- 混沌数学之Duffing(杜芬)振子
杜芬振子 Duffing oscillator是一个描写强迫振动的振动子,由非线性微分方程表示 杜芬方程列式如下: 其中 γ控制阻尼度 α控制韧度 β控制动力的非线性度 δ驱动力的振幅 ω驱动力的圆频 ...
- 混沌数学之Chua's circuit(蔡氏电路)
蔡氏电路(英语:Chua's circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为.在1983年,由蔡少棠教授发表,当时他正在日本早稻田大学担任访问学者[1].这个电路的制作 ...
- 混沌数学之Lorenz(洛伦茨)吸引子
洛伦茨吸引子是洛伦茨振子(Lorenz oscillator)的长期行为对应的分形结构,以爱德华·诺顿·洛伦茨的姓氏命名. 洛伦茨振子是能产生混沌流的三维动力系统,是一种吸引子,以其双纽线形状而著称. ...
- 混沌数学之logistic模型
logistic回归又称logistic回归分析,主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率. 相关DEMO参见:混沌数学之离散点集图形DEMO ...
- 混沌数学之Henon吸引子
Henon吸引子是混沌与分形的著名例子. 相关软件:混沌数学及其软件模拟相关代码: // http://wenku.baidu.com/view/d51372a60029bd64783e2cc0.ht ...
- 混沌数学之Rössler(若斯叻)吸引子
若斯叻吸引子(Rössler attractor)是一组三元非线性微分方程: frac{dx(t)}{dt} = -y(t)-z(t) frac{dy(t)}{dt} = x(t)+a*y(t) fr ...
- 混沌数学之ASin模型
相关软件:混沌数学之离散点集图形DEMO 相关代码: class ASinEquation : public DiscreteEquation { public: ASinEquation() { m ...
- 混沌数学之Kent模型
相关软件:混沌数学之离散点集图形DEMO 相关代码: // http://wenku.baidu.com/view/7c6f4a000740be1e650e9a75.html // 肯特映射 clas ...
- 混沌数学之Feigenbaum模型
1975年,物理学家米切尔·费根鲍姆(Mitchell Feigenbaum)发现,一个可用实验加以测 量的特殊数与每个周期倍化级联相联系.这个数大约是4.669,它与π并列成为似乎在数学 ...
随机推荐
- HTML5 Canvas游戏开发(三)lufylegend开源库件(上)
lufylegend可以解决HTML5开发游戏中会遇到的一些问题: 1.各种浏览器对于JavaScript和HTML的解析是不一致的. 2.手机浏览器和PC浏览器的区别. 3.JavaScript并非 ...
- wampserver的安装和使用
首先想说一下通常搭建WAMP平台的时候主要分为散装包搭建和集成包搭建过程. 散装包搭建就是把PHP,Apache,MySQL等下载下来,一个个的安装,其过程灰常的复杂,而且需要配置的系统变量和修改的文 ...
- pandas实战——对星巴克数据的分析
一.实验对象 实验对象为星巴克在全球的门店数据,我们可以使用pandas对其进行简单的分析,如分析每个国家星巴克的数量,根据门店数量对国家进行排序等. 二.数据分析 1.读取数据并获取数据行列数 首先 ...
- Ionic Js十:加载动作
$ionicLoading 是 ionic 默认的一个加载交互效果.里面的内容也是可以在模板里面修改. 用法 angular.module('LoadingApp', ['ionic']) .cont ...
- React Native踩坑之The SDK directory 'xxxxx' does not exist
相信和我一样,自己摸索配置环境的过程中,第一次配,很可能就遇到了这个比较简单地错误,没有配置sdk环境 解决办法 在电脑,系统环境变量中,添加一个sdk的环境变量 uploading-image-95 ...
- [代码审计]eml企业通讯录管理系统v5.0 存在sql注入
0x00 前言 上周五的时候想练练手,随便找了个系统下载下来看看. 然后发现还有VIP版本,但是VIP要钱,看了一下演示站,貌似也没有什么改变,多了个导入功能?没细看. 搜了一下发现这个系统,压根就没 ...
- 选择 React Native 的理由
转载:选择 React Native 的理由 从开始知道 React Native 到现在已经过了5个月,真实的试用也经历了三个月的时间.阅读文档开始,了解是什么,到简单的理解为什么,都是在聆听不同的 ...
- 安装部署VMware vSphere 5.5文档 (6-5) 安装配置vCenter
部署VMware vSphere 5.5 实施文档 ########################################################################## ...
- BZOJ 4945 UOJ #317 NOI2017 游戏 2-SAT 拓扑排序
http://uoj.ac/problem/317 https://www.lydsy.com/JudgeOnline/problem.php?id=4945 我现在的程序uoj的额外数据通过不了,b ...
- Codeforces.809E.Surprise me!(莫比乌斯反演 虚树)
题目链接 \(Description\) 给定一棵树,求\[\frac{1}{n(n-1)/2}\times\sum_{i\in[1,n],j\in[1,n],i\neq j}\varphi(a_i\ ...
