【Cf #503 C】Sergey's problem（有趣的构造）

感觉这种构造题好妙啊，可我就是想不到诶。

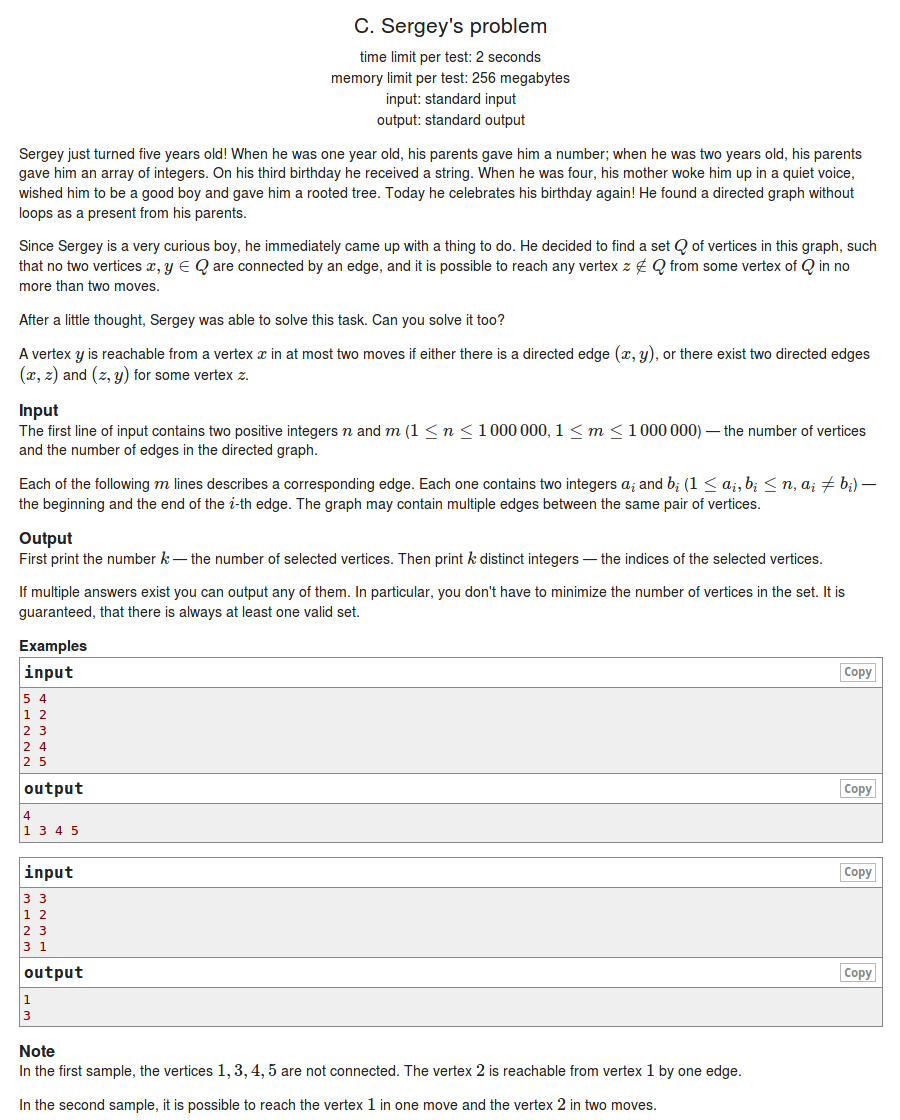
给出一张无自环的有向图，回答一个独立集，使得图中任意一点都可以被独立集中的某一点两步之内走到。

具体构造方案如下：

1. 下标从小到大枚举点，如果该点没有任何标记，则将其标记为$-1$，即答案的候选点，并把它能一步走到的未访问的点标记为$1$，即不会成为答案的点。
2. 下标从大到小进行第二次枚举，如果该点被标为$-1$并且没有被丢弃，则选则该点，并把它能一步走到的点丢弃。

我们来考虑它的正确性：

显然它是一个独立集。唯一的问题在与它有可能出现两个同为$-1$的点相连（事实上他们组成的是一个$Dag$），这时注意到有出边的那个点的标号一定比较大，我们在计算答案时一定会先选这个点，然后就不会选有入边的那个点了。

每个点都能被两步内走到。如果它是被标为$-1$的点却不在答案中，那一定存在一个$-1$点能一步到达它，由上述可知。如果它是一个$1$点，那一定有一个$-1$点与它直接相连，两步内就一定能走到了。

#include <cstdio>
#include <vector>

const int N = ;

int n, m, vis[N], usd[N];
std::vector<int> g[N], ans;

int main() {
  scanf("%d%d", &n, &m);
  for (int i = , x, y; i <= m; ++i) {
    scanf("%d%d", &x, &y);
    g[x].push_back(y);
  }
  for (int i = ; i <= n; ++i) {
    if (vis[i] != ) continue;
    vis[i] = -;
    for (int v : g[i]) if (vis[v] == ) vis[v] = ;
  }
  for (int i = n; i >= ; --i) {
    if (vis[i] != - || usd[i]) continue;
    ans.push_back(i);
    for (int v : g[i]) usd[v] = ;
  }
  printf("%lu\n", ans.size());
  for (int v : ans) printf("%d ", v);

  return ;
}