【模板】缩点（Tarjan算法）/洛谷P3387

题目链接

https://www.luogu.com.cn/problem/P3387

题目大意

给定一个 \(n\) 个点 \(m\) 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。

允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

题目解析

1. 强连通

强连通：有向图 \(D(V,E)\) 两点 \(a,b\) 互相可达，称 \(a,b\) 强连通。

强连通分量：有向图 \(D\) 的点集子集 \(\mathrm{v}\) 两两可达，且 \(\mathrm{v}\) 是极大的（增加任意新点即不满足条件），称 \(\mathrm{v}\) 为 \(D\) 的一个强连通分量。

定理：有向图 \(D\) 可唯一划分为若干强连通分量 \(\mathrm{v_1,v_2,...,v_n}\) 。

1. 缩点

缩点，即将有向图 \(D\) 划分为若干强连通分量 \(\mathrm{v_1,v_2,...,v_n}\) 。

将每个强连通分量视作一个点，这些点组成点集 \(V'\) ，强连通分量之间的边组成边集 \(E'\) ，得到一张新的有向图 \(D'(V',E')\)。

定理：有向图 \(D'\) 无环 \((DAG)\)。

1. \(Tarjan\) 算法

\(Tarjan\) 算法通过一遍 \(DFS\) ，实现缩点的过程。

其原理简单概括为：

对于一个点 \(p\) , \(DFS\) 记录每个点进入搜索的时间戳(搜索顺序) \(\mathrm{dfn}[p]\)，以及是否仍在栈中 \(\mathrm{inStack}[p]\)。

\(DFS\) 找不到新的路径即走到了尽头，记录从该点能到达的时间戳最早的点的时间 \(\mathrm{low}[p]=\min{\mathrm{dfn}[p']}\)，那么 \(p\) 和 \(p'\) 之间所有在栈中的点都属于同一个强连通分量。

伪代码如下：

Tarjan(u)
{
    dfn[u] = low[u] = ++Index
    Stack.push(u)
    for each (u->v) in E
        if (v is not visited)
            Tarjan(v)
            low[u] = min(low[u], low[v])
        else if (v in Stack)
            low[u] = min(low[u], dfn[v])
    if (dfn[u] == low[u])         //如果节点u是强连通分量的根
          ++cnt                   //增加强连通分量个数
          repeat
              v = Stack.pop
              add v into set[cnt] //将v退栈，为该强连通分量中一个顶点
          until (u == v)
}

时间复杂度： \(O(n+m)\)

可以通过下面这个例子，形象地体会一下算法流程：

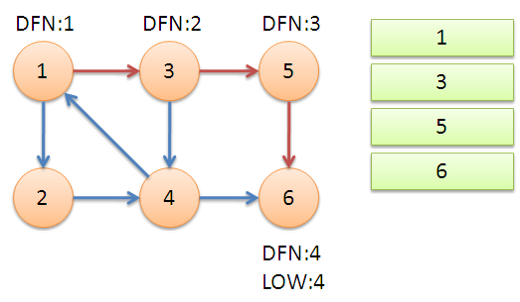
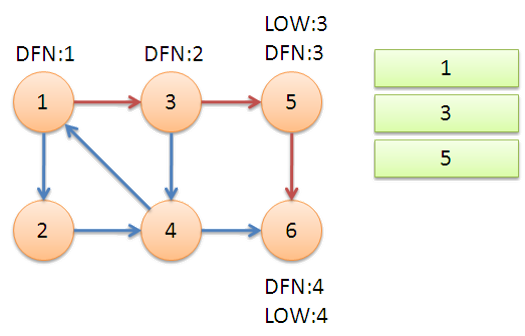
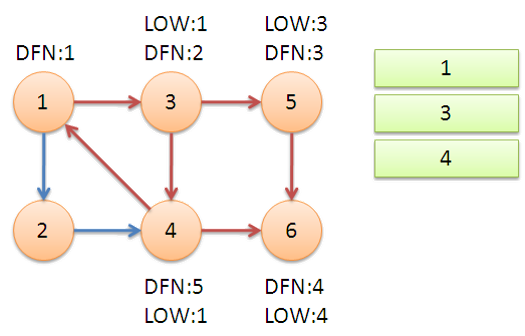
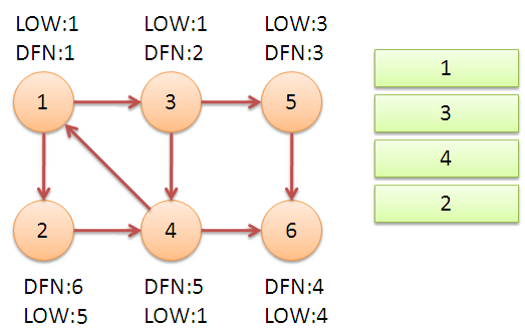
1. 原题目解析

将原有向图 \(D\) 缩点简化为新的有向无环图 \(D'\)，新的点权为强连通分量中的点权之和，求 \(D'\) 的一条点权最大路径，只需从各顶点出发一遍 \(DFS\) 即可。

简单说明一下参考代码：

dfn[i], inStack[i]意义同上。
e[i]记录从i点出发的边集，g[k]记录第k个强连通分量的点集。
f[i]意义同low[i]。
u[i]记录原图每个点的点权。
w[k]记录第k个强连通分量的联合点权。
ans[i]记录从i点出发的路径最大点权（记忆化搜索）。
mp为某个点i属于哪个强连通分量的索引(mp{f[i] -> k})。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e4+5;
int f[N], dfn[N], inStack[N], w[N], ans[N], u[N];
int n, m, idx=0, cnt=0;
vector <int> e[N], g[N];
map <int, int> mp;
stack <int> stk;

int tarjan(int x)
{
    int b, t;
    dfn[x] = f[x] = ++idx;
    stk.push(x);
    inStack[x] = 1;
    for (int i=0; i<e[x].size(); i++)
    {
        b = e[x][i];
        if (!dfn[b]) {
            tarjan(b);
            f[x] = min(f[b], f[x]);
        }
        else if (inStack[b]) {
            f[x] = min(f[b], f[x]);
        }
    }
    if (dfn[x] == f[x]) {
        mp.insert(pair<int, int>(f[x], ++cnt));
        w[cnt] = 0;
        do {
            t = stk.top();
            stk.pop();
            inStack[t] = 0;
            g[cnt].push_back(t);
            f[t] = f[x];
            w[cnt] += u[t];
        } while (x != t);
    }
}
int find(int x) {return f[x] == x ? dfn[x] : f[x] = find(f[dfn[x]]);}
int dfs(int x)
{
    int k = 0;
    ans[x] = w[x];
    for (int i=0; i<g[x].size(); ++i)
    {
        for (int j=0; j<e[g[x][i]].size(); ++j)
        {
            int b = mp[f[e[g[x][i]][j]]];
            if (ans[b] == -1) dfs(b);
            if (b != x) k = max(k, ans[b]);
        }
    }
    return ans[x] = ans[x] + k;
}
int main()
{
    int i, a, b;
    scanf("%d%d", &n, &m);
    for (i=1; i<=n; ++i) scanf("%d", &u[i]);
    for (i=1; i<=m; ++i) {
        scanf("%d%d", &a, &b);
        if (a == b) m--, i--;
        else e[a].push_back(b);
    }
    for (i=1; i<=n; ++i) if (!dfn[i]) tarjan(i);
    int res = 0;
    for (i=1; i<=cnt; ++i) ans[i] = -1;
    for (i=1; i<=cnt; ++i){
        if (ans[i] == -1) dfs(i);
        res = max(res, ans[i]);
    }
    printf("%d\n", res);
    return 0;
}

感谢阅读！