算法leetcode二分算法

二分算法通常用于有序序列中查找元素：

有序序列中是否存在满足某条件的元素；
有序序列中第一个满足某条件的元素的位置；
有序序列中最后一个满足某条件的元素的位置。

思路很简单，细节是魔鬼。

一.有序序列中是否存在满足某条件的元素

首先，二分查找的框架：

def binarySearch(nums, target):

    l = 0   #low

    h = ... #high



    while l...h:

        m = (l + (h - l) / 2)  #middle,防止h+l溢出

        if nums[m] == target:

            ...

        elif nums[m] < target:

            l = ...      #缩小边界

        elif nums[m] > target:

            h = ...

    return ...    #查找结果

其次，最基本的查找有序序列中的一个元素

 def binarySearch(nums, target):

     l = 0

     h = len(nums) - 1

     while l <= h :

         m = (l + (h - l) / 2)

         if nums[m] == target:

             return m

         elif nums[m] < target:

             l = m + 1

         elif nums[m] > target:

             h = m - 1

      return -1

循环的条件为什么是 <=，而不是 < ？

答：要保证能遍历到数组的第一个元素和最后一个元素。因为初始化 h 的赋值是 len(nums) - 1，即最后一个元素的索引，而不是 len(nums)。

这二者可能出现在不同功能的二分查找中，区别是：前者相当于两端都闭区间 [l, h]，后者相当于左闭右开区间 [l, h)，因为索引大小为 len(nums) 是越界的。

我们这个算法中使用的是 [l, h] 两端都闭的区间。这个区间就是每次进行搜索的区间，我们不妨称为「搜索区间」(search space)。

此算法有什么缺陷？

答：至此，你应该已经掌握了该算法的所有细节，以及这样处理的原因。但是，这个算法存在局限性。

比如说给你有序数组 nums = [1,2,2,2,3]，target = 2，此算法返回的索引是 2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理的。

这样的需求很常见。你也许会说，找到一个 target 索引，然后向左或向右线性搜索不行吗？可以，但是不好，因为这样难以保证二分查找对数级的时间复杂度了。

我们后续的算法就来讨论这两种二分查找的算法。

二、寻找一个数（基本的二分搜索）

这个场景是最简单的，可能也是大家最熟悉的，即搜索一个数，如果存在，返回其索引，否则返回 -1。

def binarySearch([] nums,  target):

    l = 0

    h = len(nums) - 1



    while l <= h:

        m = (l + (h - l) / 2)

        if nums[m] == target:

            return m

        elif nums[m] < target:

            l = m + 1

        elif nums[m] > target:

            h = m - 1

    return -1

1. 为什么 while 循环的条件中是 <=，而不是 < ？

答：因为初始化 h 的赋值是 len(nums) - 1，即最后一个元素的索引，而不是 len(nums)。

我们这个算法中使用的是 [l, h] 两端都闭的区间。这个区间就是每次进行搜索的区间，我们不妨称为「搜索区间」(search space)。

什么时候应该停止搜索呢？当然，找到了目标值的时候可以终止：

if nums[m] == target

    return m

但如果没找到，就需要 while 循环终止，然后返回 -1。那 while 循环什么时候应该终止？搜索区间为空的时候应该终止，意味着你没得找了，就等于没找到嘛。

while(l <= h)的终止条件是 l == h + 1，写成区间的形式就是 [h + 1, h]，或者带个具体的数字进去 [3, 2]，可见这时候搜索区间为空，因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的，直接返回 -1 即可。

while(l < h)的终止条件是 l == h，写成区间的形式就是 [h, h]，或者带个具体的数字进去 [2, 2]，这时候搜索区间非空，还有一个数 2，但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了，索引 2 没有被搜索，如果这时候直接返回 -1 就可能出现错误。

当然，如果你非要用 while(l < h) 也可以，我们已经知道了出错的原因，就打个补丁好了：

while l < h:

    # ...

return nums[l] == target ? l : -1

2. 为什么 l = m + 1，h = m - 1？我看有的代码是 h = m 或者 l = m，没有这些加加减减，到底怎么回事，怎么判断？

答：这也是二分查找的一个难点，不过只要你能理解前面的内容，就能够很容易判断。

刚才明确了「搜索区间」这个概念，而且本算法的搜索区间是两端都闭的，即 [l, h]。那么当我们发现索引 m 不是要找的 target 时，如何确定下一步的搜索区间呢？

当然是去搜索 [l, m - 1] 或者 [m + 1, h] 对不对？因为 m 已经搜索过，应该从搜索区间中去除。

3. 此算法有什么缺陷？

答：至此，你应该已经掌握了该算法的所有细节，以及这样处理的原因。但是，这个算法存在局限性。

我们后续的算法就来讨论这两种二分查找的算法。

三、寻找左侧边界的二分搜索

直接看代码，其中的标记是需要注意的细节：

def l_bound(nums,  target):

    if len(nums) == 0 return -1

     l = 0

     h = len(nums)



    while l < h

         m = int(l + (h - l) / 2)

        if nums[m] == target:

            h = m

        elif nums[m] < target:

            l = m + 1

        elif nums[m] > target:

            h = m

    return l

为什么 while(l < h) 而不是 <= ?

答：用相同的方法分析，因为初始化 h = len(nums) 而不是 len(nums) - 1 。因此每次循环的「搜索区间」是 [l, h) 左闭右开。

while(l < h) 终止的条件是 l == h，此时搜索区间 [l, l) 恰巧为空，所以可以正确终止。

为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎么办？

答：因为要一步一步来，先理解一下这个「左侧边界」有什么特殊含义：

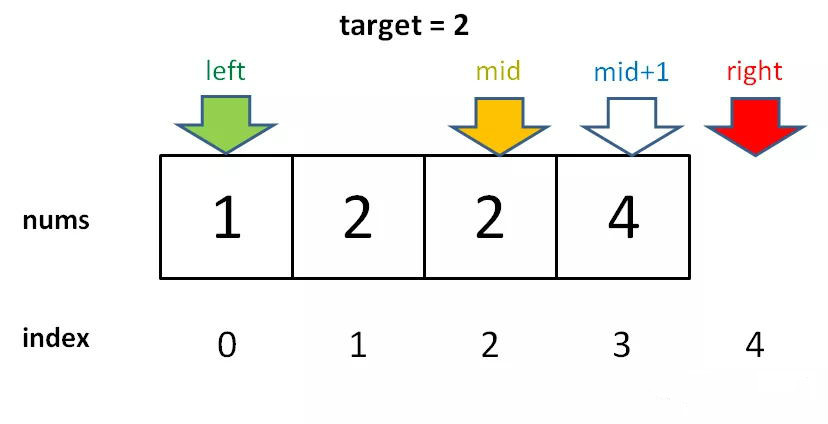
对于这个数组，算法会返回 1。这个 1 的含义可以这样解读：nums 中小于 2 的元素有 1 个。

比如对于有序数组 nums = [2,3,5,7], target = 1，算法会返回 0，含义是：nums 中小于 1 的元素有 0 个。如果 target = 8，算法会返回 4，含义是：nums 中小于 8 的元素有 4 个。

综上可以看出，函数的返回值（即 l 变量的值）取值区间是闭区间 [0, len(nums)]，所以我们简单添加两行代码就能在正确的时候 return -1：

while l < h:

    #...



# target 比所有数都大

if l == len(nums) return -1

# 类似之前算法的处理方式

return nums[l] == target ? l : -1

3. 为什么 l = m + 1，h = m ？和之前的算法不一样？

答：这个很好解释，因为我们的「搜索区间」是 [l, h) 左闭右开，所以当 nums[m] 被检测之后，下一步的搜索区间应该去掉 m 分割成两个区间，即 [l, m) 或 [m + 1, h)。

4. 为什么该算法能够搜索左侧边界？

答：关键在于对于 nums[m] == target 这种情况的处理：

    if nums[m] == target:

        h = m

可见，找到 target 时不要立即返回，而是缩小「搜索区间」的上界 h，在区间 [l, m) 中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。

5. 为什么返回 l 而不是 h？

答：返回l和h都是一样的，因为 while 终止的条件是 l == h。

四、寻找右侧边界的二分查找

寻找右侧边界和寻找左侧边界的代码差不多，只有两处不同，已标注：

def h_bound(nums,  target):

    if len(nums) == 0  return -1

    l = 0

    h = len(nums)



    while l < h:

        m = int((l + h) / 2)

        if nums[m] == target:

            l = m + 1

        elif nums[m] < target:

            l = m + 1

        elif nums[m] > target:

            h = m

    return l - 1

1. 为什么这个算法能够找到右侧边界？

答：类似地，关键点还是这里：

    if nums[m] == target:
        l = m + 1

当 nums[m] == target 时，不要立即返回，而是增大「搜索区间」的下界 l，使得区间不断向右收缩，达到锁定右侧边界的目的。

2. 为什么最后返回 l - 1 而不像左侧边界的函数，返回 l？而且我觉得这里既然是搜索右侧边界，应该返回 h 才对。

答：首先，while 循环的终止条件是 l == h，所以 l 和 h 是一样的，你非要体现右侧的特点，返回 h - 1 好了。

至于为什么要减一，这是搜索右侧边界的一个特殊点，关键在这个条件判断：

    if nums[m] == target:
        l = m + 1

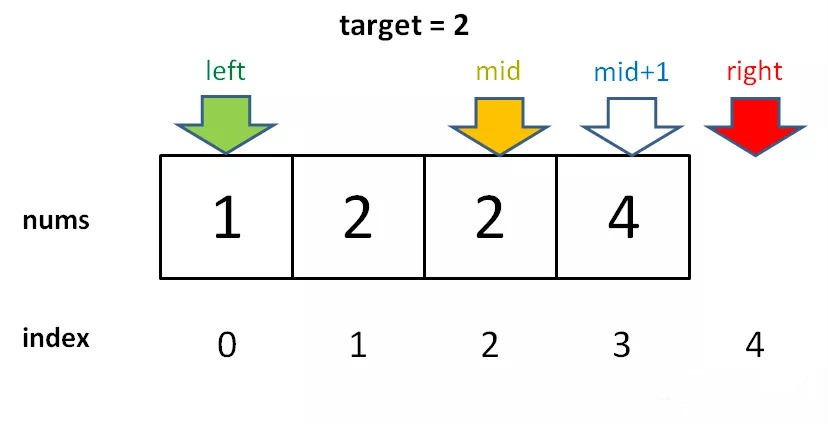
因为我们对 l 的更新必须是 l = m + 1，就是说 while 循环结束时，nums[l] 一定不等于 target 了，而 nums[l - 1]可能是target。

至于为什么 l 的更新必须是 l = m + 1，同左侧边界搜索，就不再赘述。

3. 为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎么办？

答：类似之前的左侧边界搜索，因为 while 的终止条件是 l == h，就是说 l 的取值范围是 [0, len(nums)]，所以可以添加两行代码，正确地返回 -1：

while l < h:

# ...



if l == 0 return -1

return nums[l-1] == target ? (l-1) : -1

五、最后总结

先来梳理一下这些细节差异的因果逻辑：

第一个，最基本的二分查找算法：

因为我们初始化 h = len(nums) - 1
所以决定了我们的「搜索区间」是 [l, h]
所以决定了 while (l <= h)
同时也决定了 l = m+1 和 h = m-1

因为我们只需找到一个 target 的索引即可
所以当 nums[m] == target 时可以立即返回

第二个，寻找左侧边界的二分查找：

因为我们初始化 h = len(nums)
所以决定了我们的「搜索区间」是 [l, h)
所以决定了 while (l < h)
同时也决定了 l = m+1 和 h = m

因为我们需找到 target 的最左侧索引
所以当 nums[m] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界

第三个，寻找右侧边界的二分查找：

因为我们初始化 h = len(nums)
所以决定了我们的「搜索区间」是 [l, h)
所以决定了 while (l < h)
同时也决定了 l = m+1 和 h = m

因为我们需找到 target 的最右侧索引
所以当 nums[m] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界

又因为收紧左侧边界时必须 l = m + 1
所以最后无论返回 l 还是 h，必须减一

如果以上内容你都能理解，那么恭喜你，二分查找算法的细节不过如此。

通过本文，你学会了：

1. 分析二分查找代码时，不要出现 else，全部展开成 elif 方便理解。

2. 注意「搜索区间」和 while 的终止条件，如果存在漏掉的元素，记得在最后检查。

3. 如需要搜索左右边界，只要在 nums[m] == target 时做修改即可。搜索右侧时需要减一。

就算遇到其他的二分查找变形，运用这几点技巧，也能保证你写出正确的代码。LeetCode Explore 中有二分查找的专项练习，其中提供了三种不同的代码模板，现在你再去看看，很容易就知道这几个模板的实现原理了。