Bayesian Optimization with a Finite Budget: An Approximate Dynamic Programming Approach

目录

• 概
• 主要内容

Lam R, Willcox K, Wolpert D H, et al. Bayesian Optimization with a Finite Budget: An Approximate Dynamic Programming Approach[C]. neural information processing systems, 2016: 883-891.

@article{lam2016bayesian,

title={Bayesian Optimization with a Finite Budget: An Approximate Dynamic Programming Approach},

author={Lam, Remi and Willcox, Karen and Wolpert, David H},

pages={883--891},

year={2016}}

概

贝叶斯优化中的多步优化策略. 像经典的EI方法, 就是只考虑一步, 即希望找到

\[r(\mathcal{S}_k, x_{k+1},f_{k+1})=\max \{0, f_{min}^{\mathcal{S}_k}-f_{k+1}\}
\]

的期望收益最大化的点\(x_{k+1}\)为下一个评估点.

上式中的\(f_{min}^{\mathcal{S}_k}\)是指目标函数在集合\(\mathcal{S}_k\)上的最小值.

主要内容

考虑如下动态规划, 第k步的

状态: \(\mathcal{S}_k\), 即观测到的点;

控制: \(u_k\), 且\(u_k(\mathcal{S}_k)=x_{k+1}\)

扰动: \(w_k:=f_{k+1} \sim p(f(x_{k+1})|\mathcal{S}_k)\);

设状态转移为:

\[\mathcal{S}_{k+1} = \mathcal{F}_k (\mathcal{S}_{k}, x_{k+1}, f_{k+1}) = \mathcal{S}_{k}\cup \{(x_{k+1}, f_{k+1})\}.
\]

收益(效用函数):

\[U_k(x_{k+1}; \mathcal{S} _k) = \mathbb{E}_{w_k}[r_k(\mathcal{S}_k, x_{k+1}, f_{k+1})+J_{k+1}(\mathcal{F}_k (\mathcal{S}_{k}, x_{k+1}, f_{k+1}))], \\
J_k(x_{k+1}) = \max_{x_{k+1}} U_k,\\
J_N=r_N(x_{N+1}).
\]

很自然的想法是, 我们最大化\(U_1\), 来获得所需的评估点, 但是问题是, 这个是一个嵌套的最大化优化问题， 不易求解.

本文采用rollout 算法来估计\(U_k\), 具体如下:

给定基本的决策控制\(\pi = (\pi_1, \ldots, \pi_N)\)(比如最大化EI), 为了最优化\(U_k\), 我们先选择用\(H_{k+1}\)估计\(J_{k+1}\), 其定义如下:

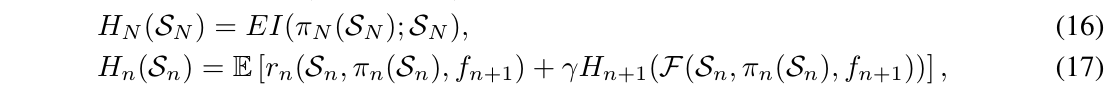
其中\(n \in \{k+1, \ldots, N-1\}\), \(\gamma \in [0, 1]\) 用以调节增量.

\(H_n\)是一个期望, 可以用Gauss-Hermite正交化估计:

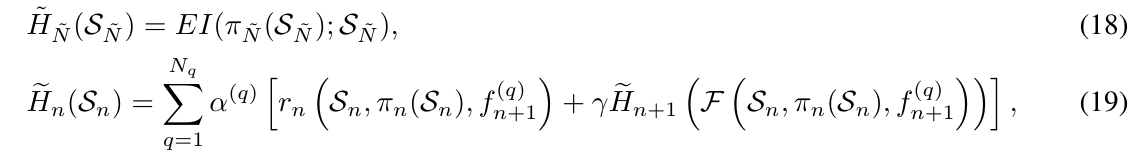
其中\(\tilde{N} = \min \{k+h, N\}\), 用以限制最大的估计步数, \(\alpha^{(q)}\)是正交系数, \(f_{n+1}^{(q)}\)是Hermite多项式的根(大概).

于是, \(U_k(x_{k+1},\mathcal{S}_k)\)便可用下式估计:

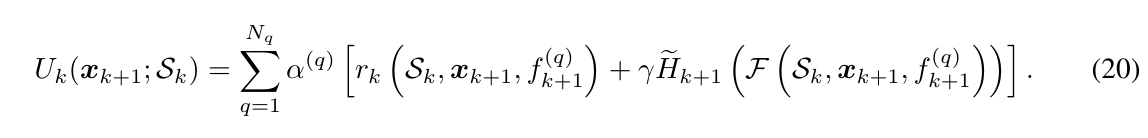
算法如下:

Input: \(h, \gamma, N, \mathcal{S}_1\);

repeat N:

• 根据(20）近似最大化\(U_k\)
• 更新\(\mathcal{S}_{k+1}=\mathcal{S}_k \cup \{(x_{k+1},f_{k+1})\}\)

out: \(f_{min}^{S_{N+1}}\).