csp-s 2021
T1 廊桥分配
当一架飞机抵达机场时，可以停靠在航站楼旁的廊桥，也可以停靠在位于机场边缘的远机位。
乘客一般更期待停靠在廊桥，因为这样省去了坐摆渡车前往航站楼的周折。
然而，因为廊桥的数量有限，所以这样的愿望不总是能实现。 机场分为国内区和国际区，国内航班飞机只能停靠在国内区，国际航班飞机只能停靠在国际区。
一部分廊桥属于国内区，其余的廊桥属于国际区。 L 市新建了一座机场，一共有 n 个廊桥。
该机场决定，廊桥的使用遵循“先到先得”的原则，
即每架飞机抵达后，如果相应的区（国内/国际）还有空闲的廊桥，就停靠在廊桥，否则停靠在远机位（假设远机位的数量充足）。
该机场只有一条跑道，因此不存在两架飞机同时抵达的情况。 现给定未来一段时间飞机的抵达、离开时刻。
请你负责将 n 个廊桥分配给国内区和国际区，使停靠廊桥的飞机数量最多。
数据范围：
1<=n<=10^5,m1+m2<=10^5
找规律，会发现在廊桥个数较少时的能够得到廊桥的飞机，在廊桥个数增加时也一定会得到廊桥！
这样就可以很容易用set来计算，每架飞机只会被清除set一次，所以是O(nlogn)。
这次考试中，kzsn很好的忘记了iterator怎么写(英语太不好了)，而且考场上也太紧张，没想出怎么替代iterator，就很伤心。
后来想到可以用 $auto$ 或者直接用 $*s1.lower_bound(x)$，便可完美避开iterator。
kzsn白给 60 分。
#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=2e5+5;
struct node{
int x, y;
bool operator<(const node&p)const{
return x < p.x;
}
}a[N], b[N];
int n, m1, m2;
int ans1[N], ans2[N];
set<node>s1, s2;
signed main()
{
scanf("%d%d%d",&n,&m1,&m2);
for(re i=1;i<=m1;++i) scanf("%d%d",&a[i].x,&a[i].y), s1.insert(a[i]);
for(re i=1;i<=m2;++i) scanf("%d%d",&b[i].x,&b[i].y), s2.insert(b[i]); for(re t=1;t<=n;++t)
{
ans1[t]=ans1[t-1];
int lst=0;
for(auto it=s1.begin();it!=s1.end();)
{
lst=(*it).y;
auto nt=s1.lower_bound((node){lst, 0});
s1.erase(it);
it=nt;
ans1[t]++;
}
}
for(re t=1;t<=n;++t)
{
ans2[t]=ans2[t-1];
int lst=0;
for(auto it=s2.begin();it!=s2.end();)
{
lst=(*it).y;
auto nt=s2.lower_bound((node){lst, 0});
s2.erase(it);
it=nt;
ans2[t]++;
}
}
int ret=0;
for(re i=0;i<=n;++i)ret=max(ret, ans1[i]+ans2[n-i]);
printf("%d", ret);
return 0;
}
T2 括号序列
给出长度 n ，星号的最长长度 k 。
ps: S 为不超过 k 个字符 * 组成的非空字符串 定义一个超级括号序列：
1. ()，(S)；
2. A，B均为超级括号序列，AB，ASB；
3. (A)
4. (SA)，(AS) 给出长度为 n 的超级括号序列，有些位置不确定。
求符合规范的超级括号序列个数。
数据范围：
n<=500
通过平时做的括号序列可以定一个状态：
$f[i][j]$ 表示区间 $[l,r]$ 的合法数。
定义 $jud[i][j]$ 表示区间 $[i,j]$ 是否能够没有括号(只由‘*’或者‘?’组成)。
$1. f[l][r] += f[l+1][r-1]$
$2. f[l][r] += (jud[l+1][r-1]==1)$
$3. if(jud[l+1][p]) f[l][r] += f[p+1][r]$
$4. if(jud[p][r] f[l][r] += f[l][p-1])$
$5. if(jud[x][y] f[l][r] += f[l][x-1]+f[y+1][r]$
大概就是这些转移！
但是我们会发现，这样得到的答案会比样例多！
理性分析一下，在 $ABC$ 这种情况下，答案会算重！
所以我们需要修改一下状态！
令 $f[l][r]$ 表示区间 $[l,r]$ 合法且 $l$ 与 $r$ 位置为左右括号且匹配；
令 $g[l][r]$ 表示区间 $[l,r]$ 合法且 $l$ 与 $r$ 位置为左右括号且不匹配；
修改后就不再会算重了！！
至于第五种转移，很明显是 O(n^4) 的，可以用前缀和优化。
#include<bits/stdc++.h>
using namespace std;
#define re register int
#define int long long const int N=505, mo=1e9+7;
int n, k;
char S[N];
int jud[N][N], f[N][N], g[N][N], faw[N], sum[N];
signed main()
{
scanf("%lld%lld",&n,&k);
scanf("%s",&S[1]);
for(re i=1;i<=n;++i)
{
jud[i][i-1]=1;
for(re j=i;j<=n;++j)
{
if(S[j]=='?' || S[j]=='*') jud[i][j]=1;
else break;
}
}
for(re j=1;j<=n;++j)
for(re i=1;i<=j+1;++i)
if(jud[i][j]){faw[j]=i;break;} for(re j=1;j<=n;++j)
{
int i=faw[j-1];
if(!i)continue;
for(;i<=j;++i)
if(!jud[i][j-1])puts("!");
}
for(re len=2;len<=n;++len)
{
for(re l=1;l<=n;++l)
{
int r=l+len-1;
if(r>n)break;
if(!((S[l]=='(' || S[l]=='?') && (S[r]==')' || S[r]=='?'))) continue; if(len == 2) {f[l][r] ++; f[l][r]%=mo; continue;} (f[l][r] += f[l+1][r-1] + g[l+1][r-1])%=mo;
if(r-l-1<=k) f[l][r] += jud[l+1][r-1];
f[l][r] %= mo;
(f[l][r]+=mo)%=mo;
for(re i=1;i<=k;++i)
if(l+i<=r && jud[l+1][l+i])
(f[l][r] += f[l+i+1][r-1]+g[l+i+1][r-1])%=mo; for(re i=1;i<=k;++i)
if(l<=r-i && jud[r-i][r-1])
(f[l][r] += f[l+1][r-i-1]+g[l+1][r-i-1]%mo)%=mo; memset(sum, 0, sizeof sum);
for(re i=l;i<=r;++i)sum[i]=(sum[i-1]+f[l][i]+g[l][i])%mo; for(re j=l;j<=r;++j)
{
if(!faw[j-1])continue;
int i=max(faw[j-1], max(j-k, l+1));
if(i<=j)
(g[l][r]+=(sum[j-1]-sum[i-2])%mo*f[j][r]%mo)%=mo;
}
}
}
printf("%lld", (f[1][n]+g[1][n]+mo+mo)%mo);
return 0;
}
这里顺便贴一个 O(n^4) 的代码，上面的正解是由下面优化过来的。
#include<bits/stdc++.h>
using namespace std;
#define re register int
#define int long long const int N=505, mo=1e9+7;
int n, k;
char S[N];
int jud[N][N], f[N][N], g[N][N], faw[N], sum[N];
signed main()
{
scanf("%lld%lld",&n,&k);
scanf("%s",&S[1]);
for(re i=1;i<=n;++i)
{
jud[i][i-1]=1;
for(re j=i;j<=n;++j)
{
if(S[j]=='?' || S[j]=='*') jud[i][j]=1;
else break;
}
}
for(re j=1;j<=n;++j)
for(re i=1;i<=j+1;++i)
if(jud[i][j]){faw[j]=i;break;} for(re j=1;j<=n;++j)
{
int i=faw[j-1];
if(!i)continue;
for(;i<=j;++i)
if(!jud[i][j-1])puts("!");
}
for(re len=2;len<=n;++len)
{
for(re l=1;l<=n;++l)
{
int r=l+len-1;
if(r>n)break;
if(!((S[l]=='(' || S[l]=='?') && (S[r]==')' || S[r]=='?'))) continue; if(len == 2) {f[l][r] ++; continue;} f[l][r] += f[l+1][r-1] + g[l+1][r-1];
if(r-l-1<=k) f[l][r] += jud[l+1][r-1];
f[l][r] %= mo;
for(re i=1;i<=k;++i)
if(l+i<=r && jud[l+1][l+i])
(f[l][r] += f[l+i+1][r-1]+g[l+i+1][r-1]%mo)%=mo; for(re i=1;i<=k;++i)
if(l<=r-i && jud[r-i][r-1])
(f[l][r] += f[l+1][r-i-1]+g[l+1][r-i-1]%mo)%=mo; for(re j=l;j<=r;++j)
{
if(!faw[j-1])continue;
int i=max(faw[j-1], max(j-k, l+1));
for(;i<=j;++i)
{
if(!(jud[i][j-1]))puts("!");
(g[l][r]+=(f[l][i-1]+g[l][i-1])%mo*f[j][r]%mo)%=mo;
}
}
}
}
printf("%lld", (f[1][n]+g[1][n])%mo);
return 0;
}
T3 回文
a1,a2,a3,...,a2n
b 一开始为空序列。
进行 2n 次操作，每次将序列 a 开头或结尾加到 b 的末尾，并从 a 中删除。
让b成为一个回文数列，如果可以，请输出字典序最小的操作方案。 数据范围：
1<=n<=5*10^5
很简单的题，只需要找到规律就可以了，可惜kzsn当时考场上不知道为什么，居然调了2h，课后却只用了半小时就ac了。
nannannan。
#include<bits/stdc++.h>
using namespace std;
#define re register int const int N=1e6+5;
char ans[505][N];
int step, mk[N], nxt[N], lst[N], n, cas;
inline bool dfs(int l, int r, int x, int y)
{
if(step==2*n)
{
printf("%s\n", ans[cas]+1);
return 1;
}
if(step>=n)
{
step++;
if(mk[x]==step)
{
ans[cas][step]='L';
if(dfs(l, r, x+1, y))return 1;
}
if(mk[y]==step)
{
ans[cas][step]='R';
if(dfs(l, r, x, y-1))return 1;
}
return 0;
}
int t;
t=l;
if(l<x && (nxt[t]==x-1 || nxt[t]==y+1))
{
ans[cas][++step]='L';
mk[nxt[t]]=2*n-step+1;
if(dfs(l+1, r, min(nxt[t], x), max(nxt[t], y)))return 1;
mk[nxt[t]]=0;
}
t=r;
if(y<r && (nxt[t]==x-1 || nxt[t]==y+1))
{
ans[cas][++step]='R';
mk[nxt[t]]=2*n-step+1;
if(dfs(l, r-1, min(nxt[t], x), max(nxt[t], y)))return 1;
mk[nxt[t]]=0;
}
return 0;
}
inline void work()
{
memset(lst, 0, sizeof lst);
memset(nxt, 0, sizeof nxt);
memset(mk, 0, sizeof mk);
scanf("%d",&n);
for(re i=1;i<=2*n;++i)lst[i]=0;
for(re i=1;i<=2*n;++i)
{
int x;
scanf("%d",&x);
if(!lst[x])lst[x]=i;
else
{
nxt[lst[x]]=i;
nxt[i]=lst[x];
}
}
for(re i=1;i<=2*n;++i)mk[i]=0;
memset(mk, 0, sizeof mk);
step=0;
ans[cas][++step]='L';
mk[nxt[1]]=2*n;
if(dfs(2, 2*n, nxt[1], nxt[1]))return; memset(mk, 0, sizeof mk);
for(re i=1;i<=2*n;++i)mk[i]=0;
step=0;
ans[cas][++step]='R';
mk[nxt[2*n]]=2*n;
if(dfs(1, 2*n-1, nxt[2*n], nxt[2*n]))return; puts("-1");return;
}
signed main()
{
int T;
scanf("%d",&T);
for(cas=1;cas<=T;++cas)work();
return 0;
}
T4 交通规则
从 k 等于2时可以看出，这道题是一道最小割问题！
但是，数据范围不允许我们网络流！
回忆起我们能够用最短路来解决对偶图这种的最小割问题。
所以，k==2 时，我们解决了。具体参照题目。
而当k变大的时候呢？
参考下图
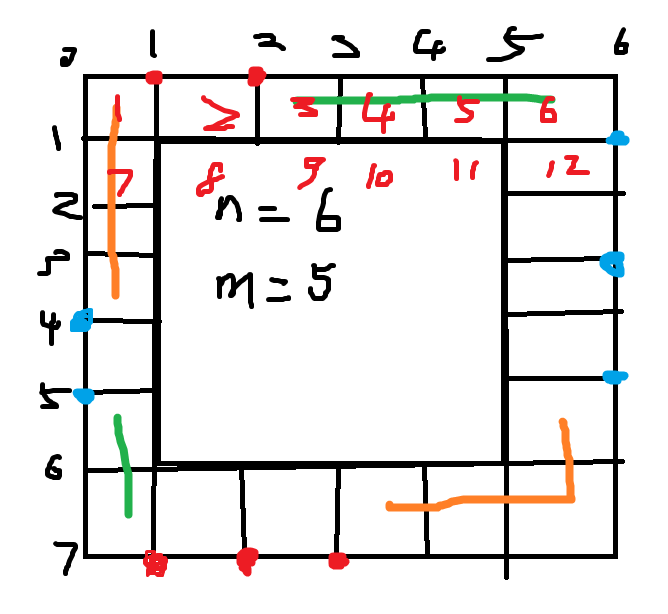
我们把从红点到蓝点的路径标记绿色，蓝点到红点标记为橙色！
所以说最短路(也就是最小割)是下面棕色的线
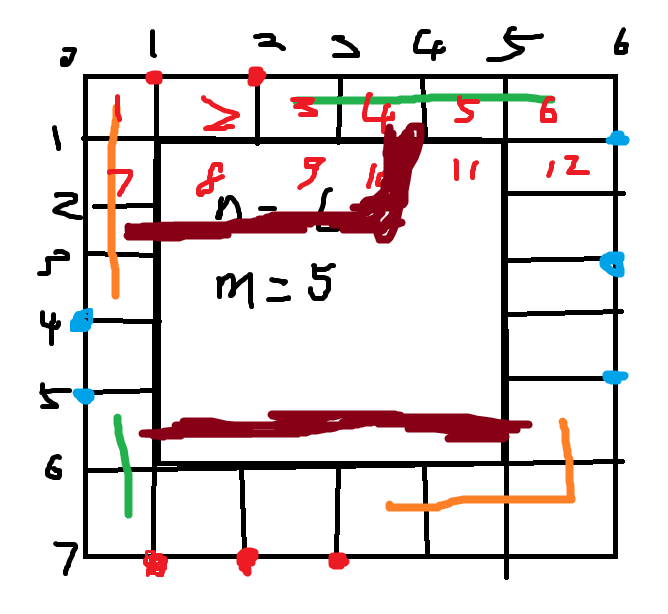
可以发现，最短路左右端点位于不同颜色上，且最短路不会相交！
我们可以提前处理出从 每段颜色到其他颜色所需的代价 $cost[i][j]$
接下来进行区间dp，如下图
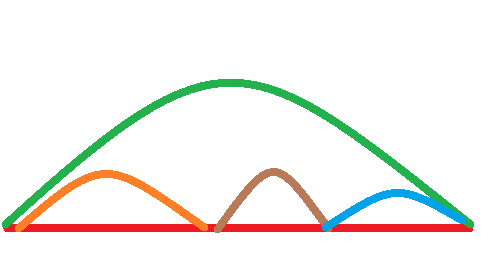
这是类似括号序列的区间dp，只不过由于是求最小值，所以不用担心去重。
#include<bits/stdc++.h>
using namespace std;
#define re register int
#define LL long long
const int N=2e6+5;
int tt=1, ed[N], nt[N], las[N], len[N];
inline void add(int x, int y, int z)
{
ed[++tt]=y;nt[tt]=las[x];las[x]=tt;len[tt]=z;
ed[++tt]=x;nt[tt]=las[y];las[y]=tt;len[tt]=z;
}
int dis[N], cost[505][505];
struct node{
int x, d;
bool operator<(const node&p)const{
return d > p.d;
}
};
vector<int>G[505];
int nid, n, m, col[N], bel[N], poi[N], a[N];
int f[505][505], mp[505][505], getname;
inline void dij(int p)
{
memset(dis, 0x3f, sizeof dis);
priority_queue<node>Q;
for(re x:G[p])Q.push((node){x,dis[x]=0});
while(!Q.empty())
{
int x=Q.top().x, d=Q.top().d;
Q.pop();
if(dis[x]!=d)continue;
for(re i=las[x];i;i=nt[i])
{
int v=ed[i];
if(dis[v]>d+len[i])
Q.push((node){v, dis[v]=d+len[i]});
}
}
for(re i=1;i<=nid;++i)
if((i+p)&1)
{
int ret=1e9;
for(re v:G[i]) ret = min(ret, dis[v]);
cost[i][p]=cost[p][i]=ret;
}
}
inline void work()
{
memset(cost, 0x3f, sizeof cost);
memset(f, 0x3f, sizeof f);
for(re i=1;i<=nid;++i)G[i].clear();
nid=0;
for(re i=1;i<=2*n+2*m;++i)
{
col[i] = -1;
len[bel[i]] = len[bel[i]^1] = 0;
}
// 清零
int K;scanf("%d",&K);
for(re i=1;i<=K;++i)
{
int x, p, t;
scanf("%d%d%d",&x,&p,&t);
col[p] = t;
len[bel[p]] = len[bel[p]^1] = x;
}
if(K==1){puts("0");return;}
int lst=-1, tmp=0;
for(re i=1;i<=2*n+2*m;++i)
if(col[i]!=-1)
{
if(lst==-1){lst = col[i];tmp = i;}
else
{
if(col[i]!=lst)
{
lst = col[i];
nid ++;
for(re j=tmp;j<i;++j)
G[nid].push_back(poi[j]);
tmp = i;
}
else tmp=i;
}
}
for(re i=1;i<=2*n+2*m;++i)
if(col[i]!=-1)
{
if(col[i]!=lst)
{
nid ++;
for(re j=tmp;j!=i;(j==2*n+2*m?j=1:j=j+1))
G[nid].push_back(poi[j]);
}
break;
}
// 处理每个颜色段
if(!nid){puts("0");return;}
for(re i=1;i<=nid;i+=2) dij(i); for(re i=1;i<=2*nid;++i)a[i]=(i>nid?i-nid:i);
// 区间dp
for(re len=2;len<=nid;++len)
for(re l=1;l<=nid;++l)
{
int r = l+len-1;
if(r>2*nid)break;
if(len == 2) {f[l][r] = cost[a[l]][a[r]];continue;}
f[l][r] = min(f[l][r], f[l+1][r-1]+cost[a[l]][a[r]]);
for(re p=l;p<r;++p) f[l][r] = min(f[l][r], f[l][p]+f[p+1][r]);
}
int ans=2e9;
for(re i=1;i<=nid;++i)
{
int j=i+nid-1;
ans=min(ans, f[i][j]);
}
printf("%d\n", ans);
}
signed main()
{
int T;
scanf("%d%d%d",&n,&m,&T);
for(re i=1;i<=n+1;i++)
for(re j=1;j<=m+1;j++)
mp[i][j]=++getname; // 给每个方格编号 for(re i=1;i<=m;++i)
{
int x=i;
add(mp[1][x], mp[1][x+1], 0);
bel[i] = tt-1; // 特殊处理最外面一层的边的编号，以便之后修改边权
poi[i] = mp[1][x+1]; // 处理第i条射线旁的方块编号
}
for(re i=m+1;i<=n+m;++i)
{
int x=i-m;
add(mp[x][m+1], mp[x+1][m+1], 0);
bel[i] = tt;
poi[i] = mp[x+1][m+1];
}
for(re i=n+m+1;i<=2*m+n;++i)
{
int x=i-n-m;
x = m+1-x;
add(mp[n+1][x], mp[n+1][x+1], 0);
bel[i] = tt;
poi[i] = mp[n+1][x];
}
for(re i=2*m+n+1;i<=2*n+2*m;++i)
{
int x=i-2*m-n;
x = n+1-x;
add(mp[x][1], mp[x+1][1], 0);
bel[i] = tt;
poi[i] = mp[x][1];
}
for(re i=1;i<n;++i)
for(re j=1;j<=m;++j)
{
int x;
scanf("%d",&x);
add(mp[i+1][j], mp[i+1][j+1], x);
} for(re i=1;i<=n;++i)
for(re j=1;j<m;++j)
{
int x;
scanf("%d",&x);
add(mp[i][j+1], mp[i+1][j+1], x);
}
while(T--)work();
return 0;
}
csp-s 2021的更多相关文章
- CSP 2021 总结
CSP 2021 总结 PJ 开题顺序:1342 应该先做 T2 ,导致我 T2 直接看错 T1.T3 T1 :直接推规律即可,考场的想法应该正确 T3 :好家伙直接 map 走起 T2 最崩溃的来了 ...
- 【游记】CSP 2021 J2
这次是第一次参加CSP的复赛,所以考的就很LJ. \(DAY-\infty\) 到 \(DAY-14\) 知道了自己苟过了初赛,像个SB一样. (我初赛66分,旁边那位63.5,cao着线过去的) \ ...
- CSP 2021 游记
\(\text{Day -INF}\) 看见了 \(\text{SCP2021}\) 的报名通知,想着应该教练会让我们统一报名,就没放在心上 然后-- 然后过了二十多天教练根本没有提报名的事情,搞得我 ...
- 2021.10.19 CSP 模拟赛 总结
T1 题意: \(n\) 个人摘苹果,跳起高度为 \(a_i\),苹果高度为 \(h_i\),高度小的先摘,摘了就没了 直接排序+双指针,复杂度 \(O(n+m)\) T2 题意:要轰炸一个有向图的所 ...
- [游记]CSP 2021 J/S
这一次,也许是我的OI生涯的转折点了--能过,学习OI的时间就不会减少:但不能过,就会减少学习OI的时间-- 上午(S组) 6:00起床.去吃早餐,结果因为边喝粥边喝牛奶导致肚子疼.(我在这里劝大家, ...
- CSP-J 2021 游记
今年是本人第一次参加CSP组的竞赛. Day 0 晚上复习了几套初赛试卷,做到晚上十点多结束.其实暑假已经做过不少了. Day 1 早上继续复习noip历年真题,在洛谷有题上面自己做题,一向只能考十几 ...
- 【OWASP TOP10】2021年常见web安全漏洞TOP10排行
[2021]常见web安全漏洞TOP10排行 应用程序安全风险 攻击者可以通过应用程序中许多的不同的路径方式去危害企业业务.每种路径方法都代表了一种风险,这些风险都值得关注. 什么是 OWASP TO ...
- CSP J/S 初赛总结
CSP J/S 初赛总结 2021/9/19 19:29 用官方答案估计 J 涂卡的时候唯一的一支 2B 铅笔坏了,只能用笔芯一个个涂 选择 \(-6\ pts\) 判断 \(-3\ pts\) 回答 ...
- CSP的今世与未来
一.从两个工具说起 最近Google又推出了两款有关CSP利用的小工具,其一为CSP Evaluator,这是一个能够评估你当前输入的CSP能否帮助你有效避免XSS攻击的工具,其用法非常简单,在输入框 ...
- windows2003安装证书服务:csp配置不正确、您没有此密钥容器的写访问权限
1.填写CA名称后在生成密钥时提示:csp配置不正确或安装不完整. 原因:可能的原因为CS服务(Crysptographic Service)没有启动 . ps:该服务依赖RPC服务,但RP ...
随机推荐
- AQS快速入门
一.模板方法模式 父子类多态,父类中用一个方法调用执行所有所需要的方法: 父类: 子类: 主线程执行时候调用父类的模板方法: 二.AQS思想 sync都是独占锁,lock显示锁也是,只有读写锁是共享锁 ...
- word域实现动态填充信息附件下载
1.问题描述:在页面上一些下载附件功能,点击触发执行下载操作时候,有些电脑的浏览器可以,有些电脑的浏览器下载不了,电脑打开弹出的下载框下载的不是一个文件,而是一个如jspx后缀名的页面,jspx后缀是 ...
- 口护万亿市场杀出的实力派 Oclean欧可林
撰文 |懂懂 编辑 | 秦言 来源:懂懂笔记 在"青年必去的电影节"上,发现了一个跟他们打成一片的智能护齿"新星". 25日,备受关注的第15届FIRST青年电 ...
- wpf内存泄漏问题
http://www.cnblogs.com/Cindys/archive/2012/05/17/2505893.html http://blogs.msdn.com/b/jgoldb/archive ...
- c++ 游戏代码(1)
迷宫代码如下: #include <iostream> #include <windows.h> #include <conio.h> using namespac ...
- 使用manacher算法解决最长回文子串问题
要解决的问题 求一个字符串最长回文子串是什么.且时间复杂度 O(N) 具体描述可参考: LeetCode_5_最长回文子串 LintCode_200_最长回文子串 暴力解法 以每个字符为中心向左右两边 ...
- 【PHP数据结构】图的遍历：深度优先与广度优先
在上一篇文章中,我们学习完了图的相关的存储结构,也就是 邻接矩阵 和 邻接表 .它们分别就代表了最典型的 顺序存储 和 链式存储 两种类型.既然数据结构有了,那么我们接下来当然就是学习对这些数据结构的 ...
- python学习笔记(十三)-python对Excel进行读写修改操作
日常工作中会遇到Excel的读写问题.我们可以使用xlwt 模块将数据写入Excel表格,使用xlrd 模块从Excel读取数据,使用xlutils模块和xlrd模块结合对Excel数据进行修改.下面 ...
- 牛客练习赛84F-牛客推荐系统开发之下班【莫比乌斯反演,杜教筛】
正题 题目链接:https://ac.nowcoder.com/acm/contest/11174/F 题目大意 给出\(n,k\)求 \[\sum_{i_1=1}^n\sum_{i_2=1}^n.. ...
- Pycharm新建模板默认添加作者时间等信息（逼格更高，好像很历害的样子）
在pycharm使用过程中,关于代码编写者的一些个人信息快捷填写,使用模板的方式比较方便. 方法如下: 1.打开pycharm,选择File-Settings 2.选择Editor--Color&am ...