R-B Tree
1、简介
R-B Tree,全称Red-Black Tree,又称为“红黑树”,为一种自平衡二叉查找树(特殊的平衡二叉树,都是在插入和删除操作时通过特定操作保持二叉树的平衡,从而获得较高的查找性能)。红黑树的每个节点上都有表示存储位的颜色,可以是红色(Red)或黑色(Black)。
红黑树特性:
- (1)每个节点要么是黑色,要么是红色。
- (2)根结点必须是黑色。
- (3)每个叶子结点是黑色(叶结点即指树尾端NIL指针或NULL结点)。
- (4)不能有连续的两个红色结点。
- (5)对于任意结点而言,其到叶结点树尾端NIL指针的每条路径都包括相同数目的黑结点。
正是红黑树的这5条性质,使得一颗n个结点的红黑树保持了Log n的高度,从而解释了红黑树的查找、插入、删除的时间复杂度最坏为O(Log n)这一结论成立的原因。
红黑树示意图一:
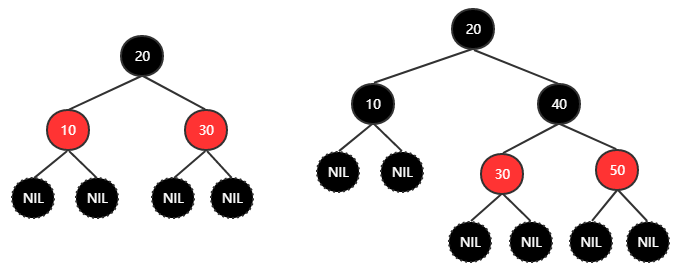
红黑树示意图二:

特性4表明:红色结点的父、左子、右子只能是黑色结点,红色和红色不能连接在一起;而黑色无论红色还是黑色都可以连在一起。(红色暴脾气互不相融,黑色和蔼可亲谁来都行)。
特性5表明:随便选一个结点,不论怎么走,走到最后叶子结点时,其经过的黑色结点数量都是相等的(所谓完全黑平衡)。
特性4、5共同决定了:最长路径的节点数量不会超过最短路径的两倍。因为黑色节点数量要一样,红色不能连着来,从而路径全黑时最短,红黑交替时最长。例如:四个黑色结点,最短:黑-黑-黑-黑(4),最长:黑-红-黑-红-黑-红-黑(7)。因为路径长度(高度)有了一定限制,所以称红黑树是有一定平衡性的,不会出现极端倾斜的情况。
2、红黑树应用
主要用来存储有序数据,时间复杂都为O(log n),效率非常高。如Java集合中的TreeMap、TreeSet、ConcurrentHashMap,C++中Set、map,以及Linux虚拟内存的管理都是用红黑树去实现的。
3、树的旋转
红黑树的基本操作是添加和删除。对红黑树进行添加和删除操作之后,红黑树会发生变化,此时可能不满足红黑树的5条特性。所以需要通过旋转来使这棵树重新成为红黑树。旋转操作包括:左旋和右旋两种操作。
仔细观察左旋与右旋的示意图,可以清晰的发现这两个操作是对称的。无论是左旋还是右旋,被旋转的树在旋转前是二叉查找树,且在旋转之后仍然是一棵二叉查找树。
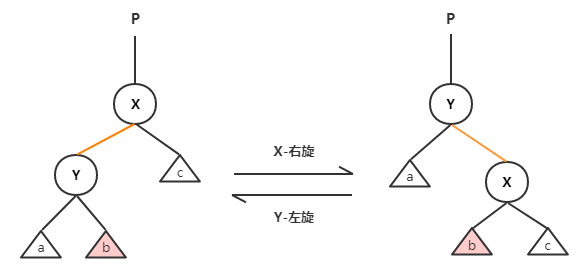
旋转后,原来“左小右大”的特点不会受到影响。影响的是左右子树的高度,右旋左子树高度-1,右子树高度+1;左旋右子树-1,左子树+1。
比如某棵树的左子树高度已经达到3,而右子树只有1,只要右旋一下,左右子树高度都将调整为2.整个树看来,高度就相当于降低了1(3->2),这样就是高度"平衡"。
注意b:
右旋前,b是挂在Y的右子,而右旋后,挂到了X的左子了;
左旋前,b是挂在X的左子,而左旋后,挂到了Y的右子了;
4、树的插入
开始之前,先约定名称:

红黑树属于二叉搜索树,插入动作也与二叉搜索树一致,只不过红黑树在插入之后,多了平衡动作(旋转与涂色)。
新插入的节点均为红色节点,因为红色不会影响路径上黑色节点的数量,保持性质4。如果父节点为黑色,就直接结束了;如果父节点为红色,则需要另外处理了。
以新插入的节点为当前平衡节点N,插入平衡大体上分为以下情形:
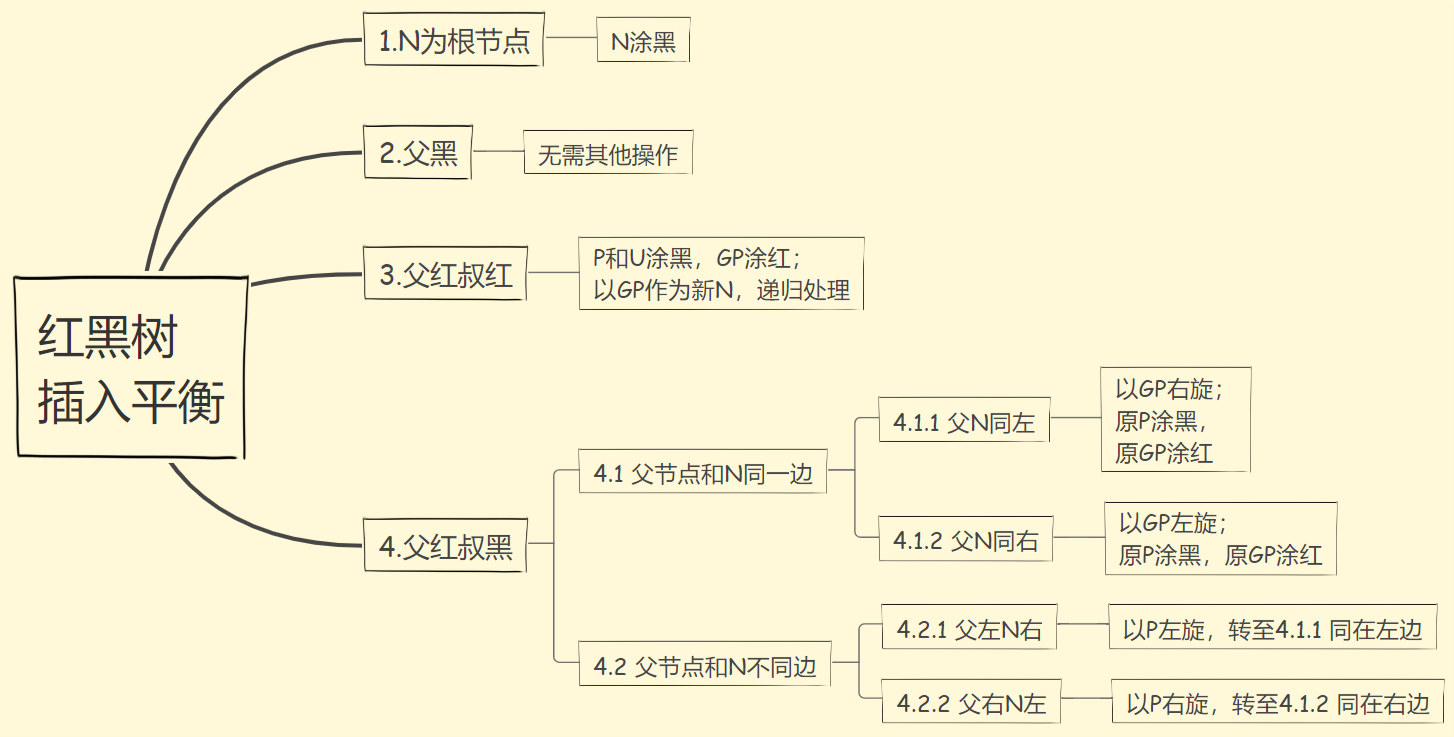
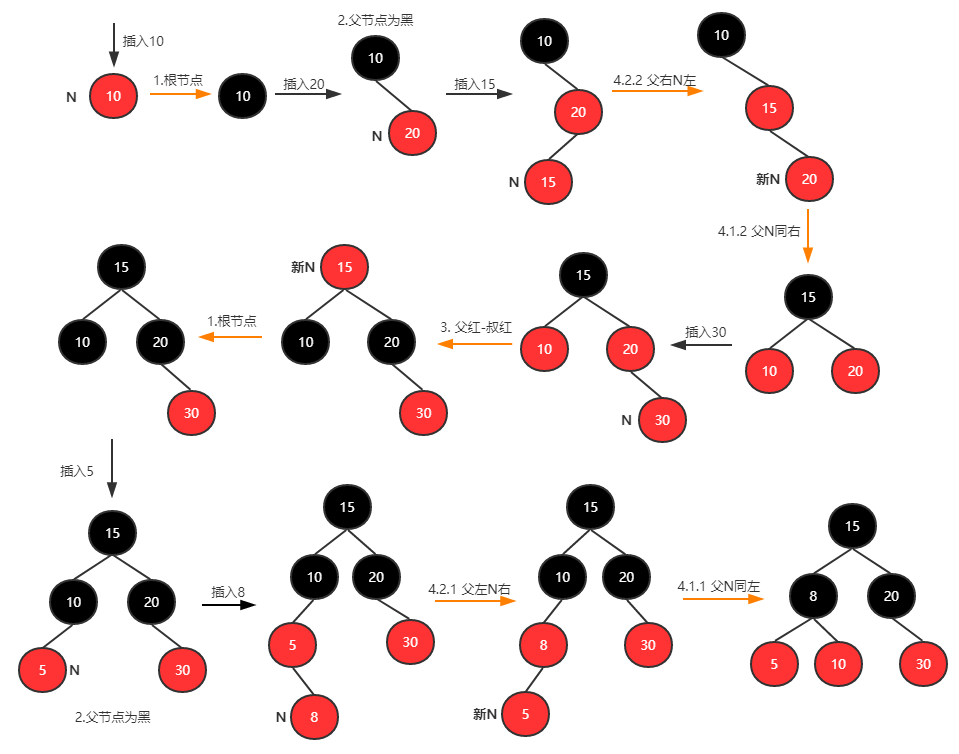
用例:插入10,20,15,30,5,8。步骤说明:
- N为根:涂黑完事;
- 父黑:啥事不用管;
- 父红叔红:父/叔涂黑,祖父涂红,然后把祖父当成新的平衡节点递归处理(我们下面平衡了,让他老人家和上面沟通吧);
- 父红叔黑:父节点和新插入节点同一边的话,扭一下就完事了(同左右旋,同右左旋,顺便涂色);不在同一边的话,先扭到同一边吧。
5)树的删除
情况分析:
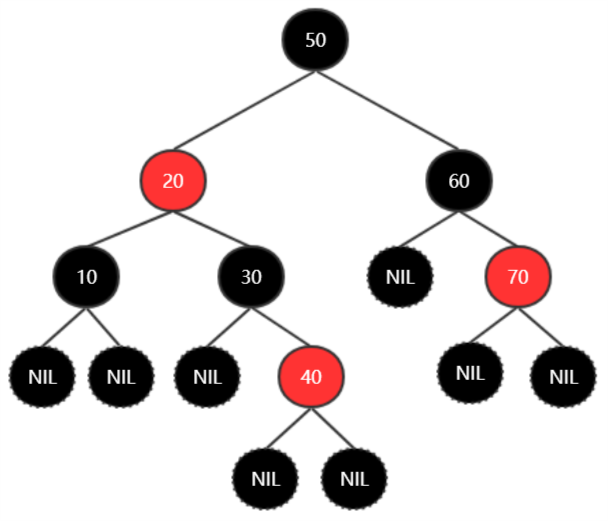
现在我们有一颗红黑树。
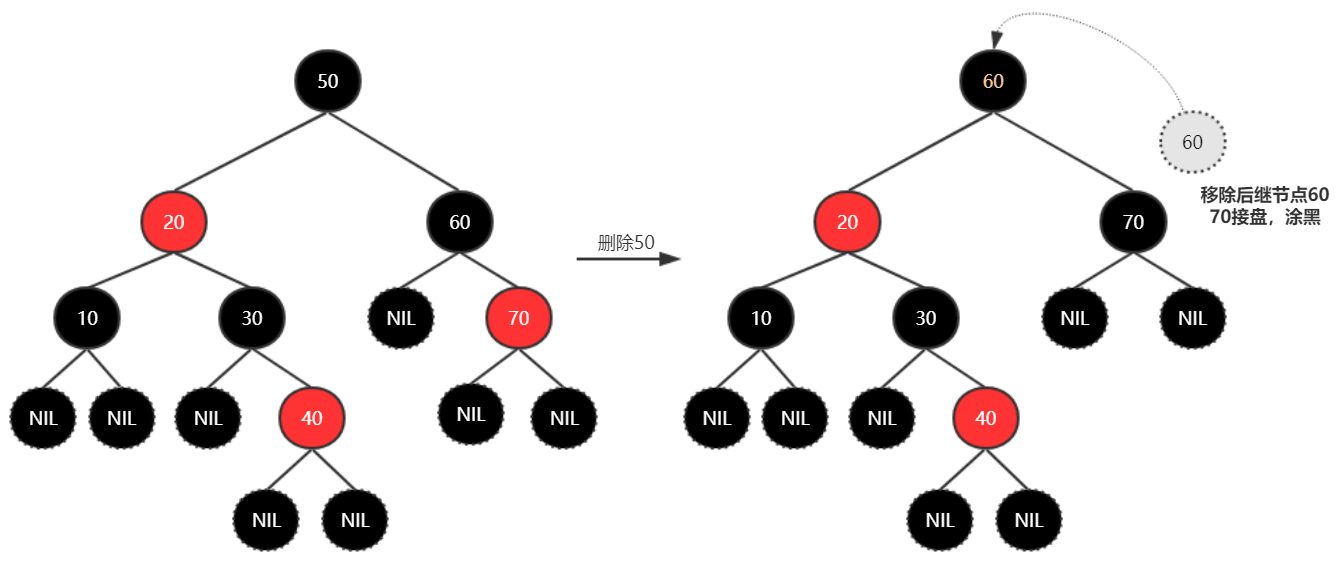
删除50
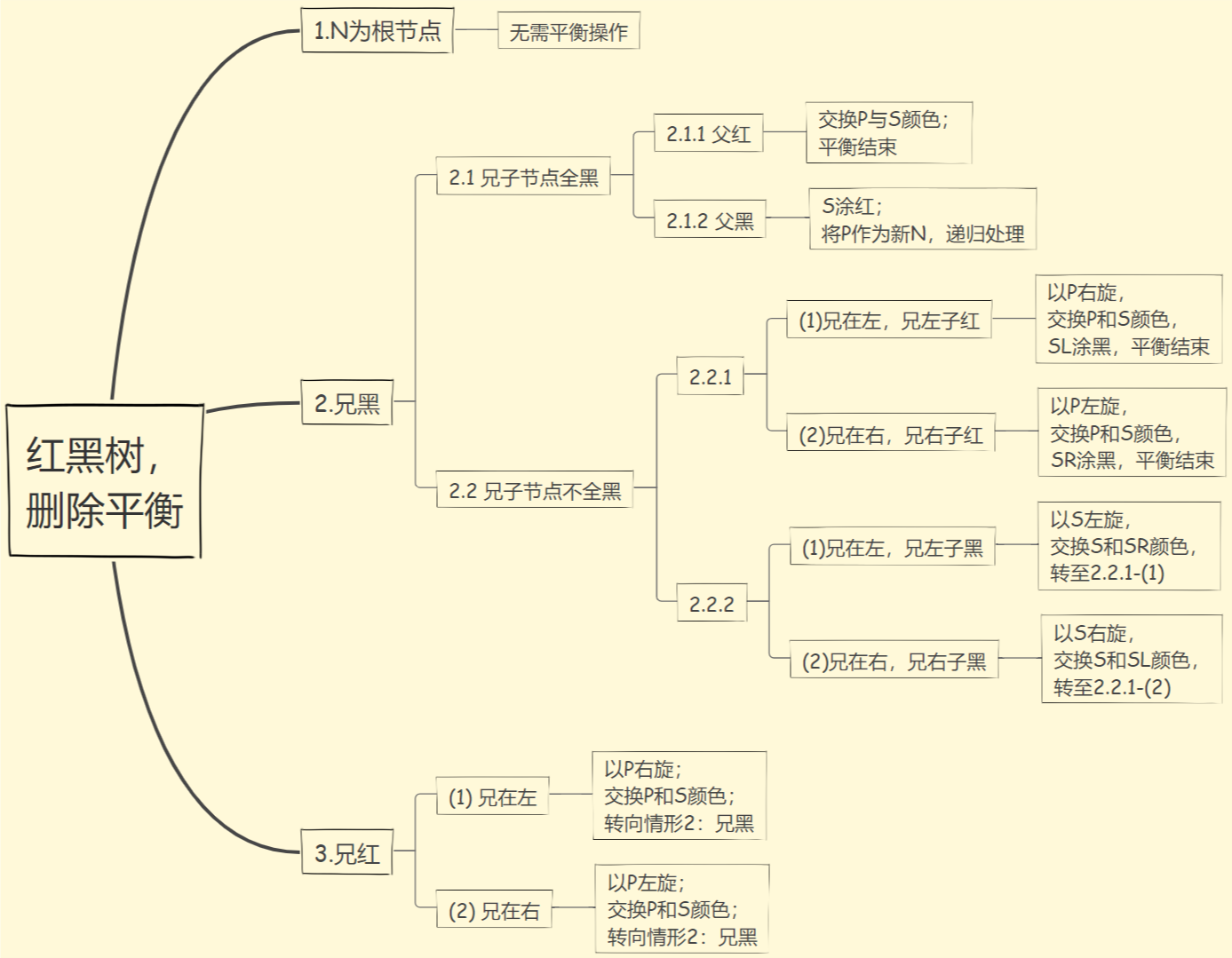
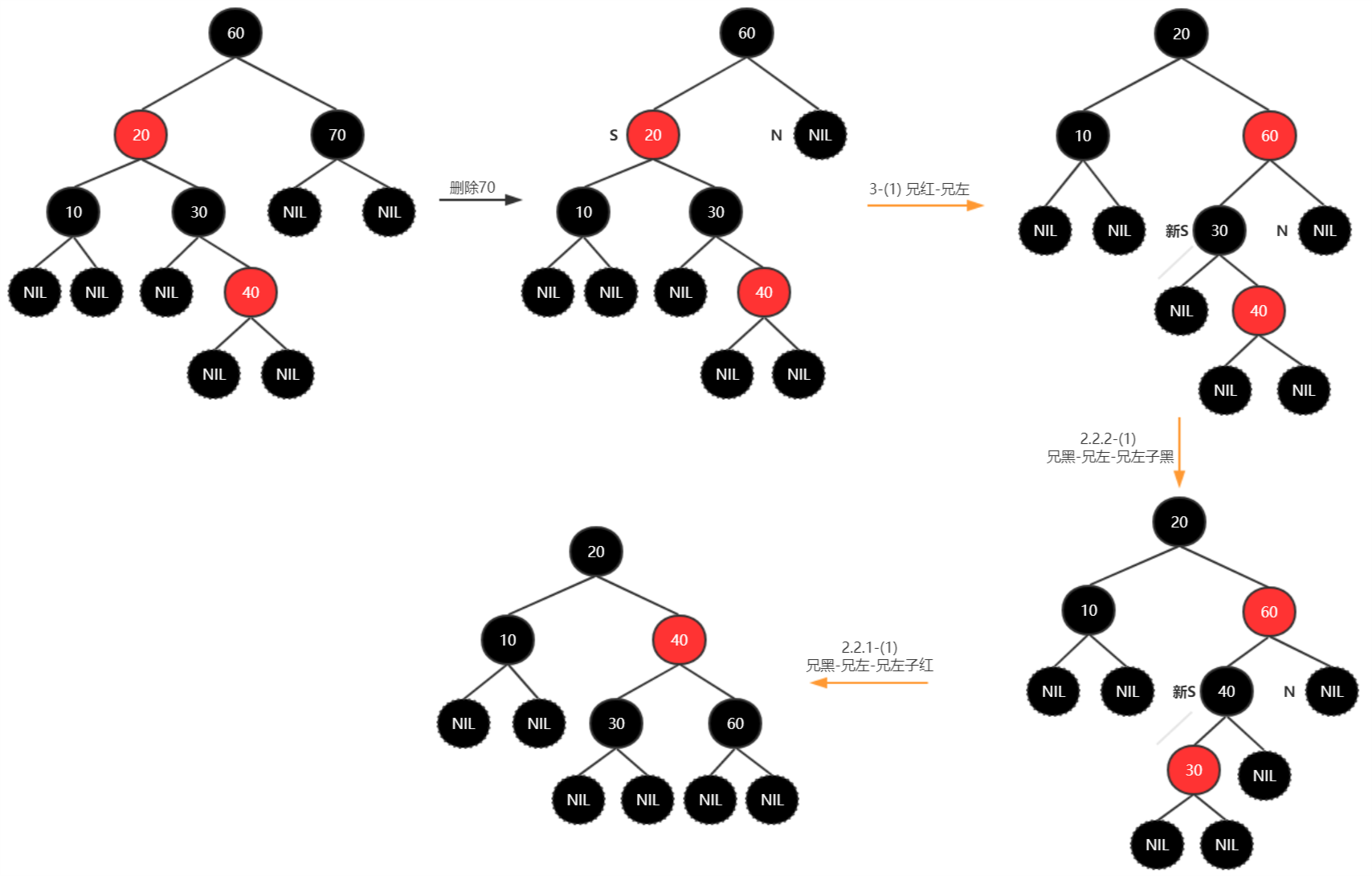
删除70,即黑色叶子节点,进行平衡:
删除60:
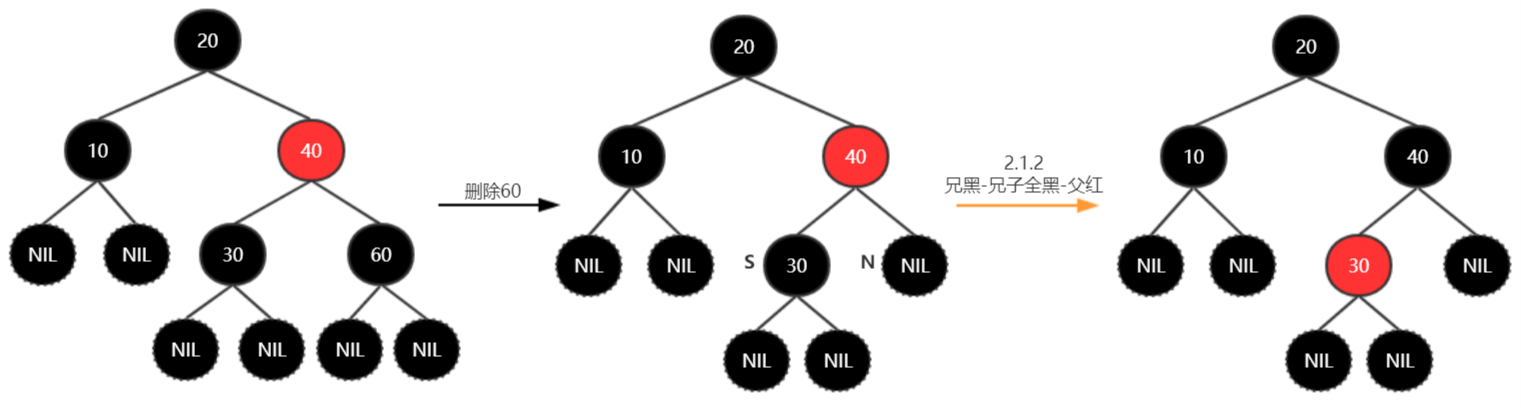
删除10:
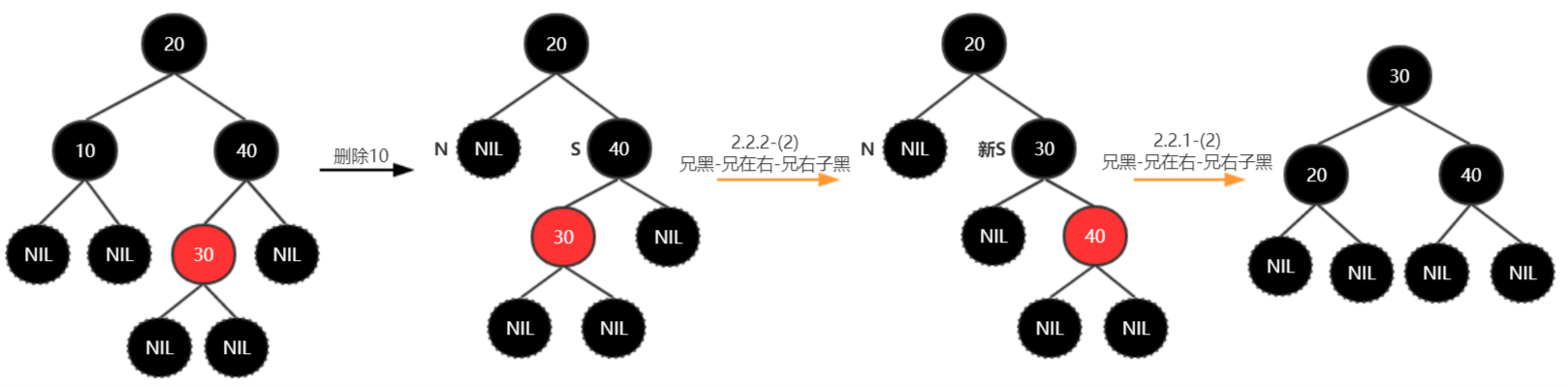
删除20
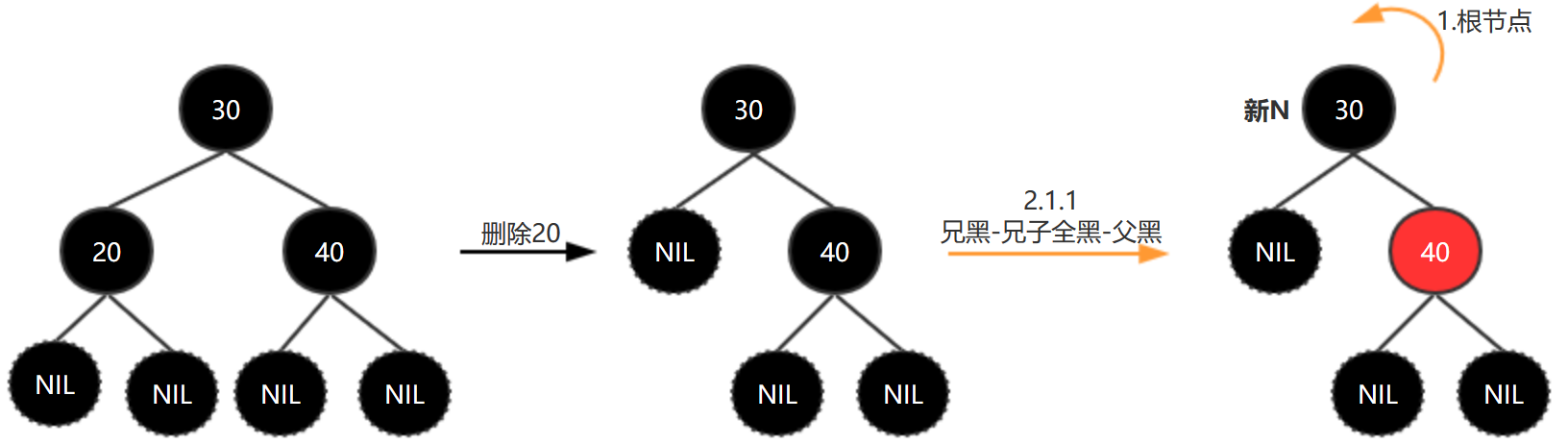
R-B Tree的更多相关文章
- SPOJ 375 Query on a tree 树链剖分模板
第一次写树剖~ #include<iostream> #include<cstring> #include<cstdio> #define L(u) u<&l ...
- tree命令的使用
有些工作在linux下完成就是比在windows下完成高效! windows和linux都有tree命令,主要功能是创建文件列表,将所有文件以树的形式列出来 windows下的tree比较垃圾,只有两 ...
- 【BZOJ-4353】Play with tree 树链剖分
4353: Play with tree Time Limit: 20 Sec Memory Limit: 256 MBSubmit: 31 Solved: 19[Submit][Status][ ...
- 【BZOJ-2648&2716】SJY摆棋子&天使玩偶 KD Tree
2648: SJY摆棋子 Time Limit: 20 Sec Memory Limit: 128 MBSubmit: 2459 Solved: 834[Submit][Status][Discu ...
- Educational Codeforces Round 6 E. New Year Tree dfs+线段树
题目链接:http://codeforces.com/contest/620/problem/E E. New Year Tree time limit per test 3 seconds memo ...
- poj 3321 Apple Tree dfs序+线段树
Apple Tree Time Limit: 2000MS Memory Limit: 65536K Description There is an apple tree outsid ...
- 泛函编程(8)-数据结构-Tree
上节介绍了泛函数据结构List及相关的泛函编程函数设计使用,还附带了少许多态类型(Polymorphic Type)及变形(Type Variance)的介绍.有关Polymorphism的详细介绍会 ...
- SPOJ QTREE Query on a tree --树链剖分
题意:给一棵树,每次更新某条边或者查询u->v路径上的边权最大值. 解法:做过上一题,这题就没太大问题了,以终点的标号作为边的标号,因为dfs只能给点分配位置,而一棵树每条树边的终点只有一个. ...
- 2014 Super Training #9 F A Simple Tree Problem --DFS+线段树
原题: ZOJ 3686 http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3686 这题本来是一个比较水的线段树,结果一个ma ...
- UPC 2224 Boring Counting (离线线段树,统计区间[l,r]之间大小在[A,B]中的数的个数)
题目链接:http://acm.upc.edu.cn/problem.php?id=2224 题意:给出n个数pi,和m个查询,每个查询给出l,r,a,b,让你求在区间l~r之间的pi的个数(A< ...
随机推荐
- 【LeetCode】735. Asteroid Collision 解题报告(Python & C++)
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 目录 题目描述 题目大意 解题方法 栈 日期 题目地址:https://leetcode ...
- Abelian Period
Abelian Period Accepts: 288 Submissions: 984 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 26 ...
- codeforce A. 2Char(水题,暴力)
今晚发了个蛇精病,然后CF了,第一题这好难啊,然而水题一个,暴力飘过. 链接http://codeforces.com/contest/593/problem/A: 题意比较难懂吗?傻逼百度都翻译不对 ...
- 小小明系列故事——游戏的烦恼(hdu 4517)
小小明系列故事--游戏的烦恼 Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)To ...
- Pydantic使用
Pydantic可以在代码运行时提供类型提示, 数据校验失败时提供友好的错误提示, 使用Python的类型注解来进行数据校验和settings管理 一般使用 from datetime import ...
- Adversarial Training with Rectified Rejection
目录 概 主要内容 rejection 实际使用 代码 Pang T., Zhang H., He D., Dong Y., Su H., Chen W., Zhu J., Liu T. Advers ...
- X86系统或intel RK主板上EDP转LVDS屏转接板|CS5211DP转LVDS设计
众所周知LVDS接口是美国NS美国国家半导体公司为克服以TTL电平方式传输宽带高码率数据时功耗大,电磁干扰大等缺点而研制的一种数字视频信号传输方式.由于其采用低压和低电流驱动方式,实现了低噪声和低功耗 ...
- JDK HttpClient 多重请求-响应的处理
HttpClient 多重请求-响应的处理 目录 HttpClient 多重请求-响应的处理 1. 简述 2. 请求响应流程图 3. 用户请求的复制 4. 多重请求处理概览 5. 请求.响应过滤的执行 ...
- 网络划分和各层协议以及webservice 浅谈
最近在公司做一些和其他外部系统接口调用的工作,遇到一些网络传输的问题,趁周末的时间记录.整理一下. 提到网络我们不得不提网络的分层架构: 我们通常听到 网络七层架构/五层架构/四层架构,但是不了解很容 ...
- Java Web程序设计笔记 • 【第10章 JSTL标签库】
全部章节 >>>> 本章目录 10.1 JSTL 概述 10.1.1 JSTL 简介 10.1.1 JSTL 使用 10.1.2 实践练习 10.2 核心标签库 10.2. ...
