NOIP模拟测试9「随·单·题」

liu_runda出的题，先$\%\%\%\%\%\%\%\%\%\%\%$为敬

随

考试时没有Qj 然后甚至没做,甚至没交

我不知道我怎么想的

这个题挺难改

你需要用到

循环矩阵快速幂,矩阵快速幂优化,打表找规律的基础

题解

首先我们可以列出来一个普通的dp式子

设f为第i次操作,操作后x变为j的概率得到$f[i][j*a[q]\%mod]=f[i-1][j]$

思考mod范围很大,那么肯定与mod无关或者矩阵快速幂,

那么我们尝试矩阵快速幂

但用了矩阵快速幂还是超时,$n^3*log$复杂度还是吃不消

观察孙金宁的嘱托

看,原根?原根可以取遍mod-1

还是很多加法

发现这是一个循环矩阵

然后我们就可以循环矩阵优化一下了

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define A 1100000
const ll mod=1e9+7;
ll c[A],a[A],b[A],al[A],base[A],res[A],qpow[A],ans[A],n,m,g,k,p,sum=0;
//al表示now存在不存在
//qpow表示j的几次方为多少
inline ll meng(ll base,ll k,ll mode){
    ll ans=1;
    for(;k;k>>=1,base=base*base%mode)
        if(k&1)
            ans=ans*base%mode;
    return ans;
}
void mult_base(){
    for(ll i=0;i<p;++i)
        for(ll j=0;j<p;++j)
            (res[j]+=base[i]*base[(j-i+p)%p])%=mod;
    for(ll i=0;i<p;++i)
        base[i]=res[i],res[i]=0;
}
void mult_ans(){
    for(ll i=0;i<p;++i)
        for(ll j=0;j<p;++j)
            (res[j]+=ans[i]*base[(j-i+p)%p])%=mod;
    for(ll i=0;i<p;++i)
        ans[i]=res[i],res[i]=0;
}
int main()
{
    scanf("%lld%lld%lld",&n,&m,&p);
    ans[0]=1;
    const ll ni=meng(n,mod-2,mod);
//    cout<<p<<endl;
    for(ll i=0;i<=1000;i++)
        al[i]=-1;
    for(ll i=1;i<p;i++){
        ll now=1,j;
        for(j=0;j<p;j++){
            if(al[now]==-1)
            {
                al[now]=j;
                qpow[j]=now;
                now=now*i%p;
//                printf("now=%lld i=%lld al[now]=%lld j=%lld\n",now,i,al[now],j);
            }
            else break;
        }
        if(j==p-1) {
            g=i;break;
        }
        else
            for(ll q=0;q<=p;q++)
                al[q]=-1;
        for(ll q=0;q<=p;q++){
//            printf("al=%lld\n",al[q]);
        }
    }

    p--;
    for(ll i=1;i<=n;i++){
        scanf("%lld",&a[i]);
//        printf("a=%lld al=%lld\n",a[i],al[a[i]]);
        a[i]=al[a[i]];
    }
    for(ll i=1;i<=n;i++){
        (base[a[i]]+=ni)%=mod;
//        printf("%lld %=%lld\n",ni,ni%mod);
    }
//    for(ll i=0;i<=p;i++){
//        cout<<a[i]<<"   "<<base[a[i]]<<endl;
//    }
    for(;m;m>>=1,mult_base())
        if(m&1)
            mult_ans();
    for(ll i=0;i<p;i++)
        sum=(sum+ans[i]*qpow[i])%mod;
    cout<<sum<<endl;
    return 0;
}

单

题解

$10\%$算法

暴力过$t==0$

$40\%$算法

gauss+暴力过前几个点

$100\%$算法

先算$t==0$

看$n^2$问题出现在那

重复计算多次距离，我们可以想个方法把自己的已经算过的存起来

现在假设我们有这样一棵树（1，2，3……代表点权，(为了方便)也代表编号）

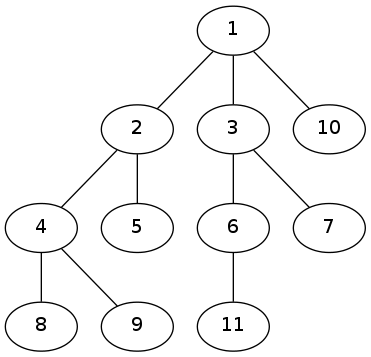
看2 和4 的关系

子树内所有的点权值贡献$-1$,子树外所有点权贡献$+1$

事实上我们可以把我们计算过的存起来。用一个前缀和思想，把子树的和算出来,我们得到1的b就可以通过$b+ -$得到$2$的$b$

那么我们只需要一次dfs处理出所有子树权值和就可以得出来所有b

式子$b[y]=b[x]-sum[y]+sum[1]-sum[y]$

这一点思想莫名像莫队,自从学了莫队我就觉得什么都是莫队

寿司这个题我就用了类似莫队思想,求出来一个$ans$然后通过$ans+-$,得到另一个$ans$

(我也颓了题解)

再看t==1的情况

看上去只能高斯消元,对吗?

实际上我们可以换种思路考虑

将$b[y]=b[x]-sum[y]+sum[1]-sum[y]$移项

得到$sum[1]-2\times sum[y]= b[y]-b[x]$

设dt数组表示两个sum之差dt[y]=b[y]-b[x]

我们可以用一次dfs求出dt那么,我们差的就只剩下sum[1] sum[y]了

仍然没法做对吗?

sum[1]其实可以求

假设1为根

$b[1]=\sum\limits_{i=2}^{n} sum[i]$

感性理解+手膜

还是这个图

每次都是路径长度$\times$权值,计算$2$的时候算了一遍$4 8 9$,计算4时又算了一遍$8 9$,路径每一个点上会被计算它到根节点之间节点个数(其实就是边数),所以最终得到的就是b[1]

同样,我们处理出来dt,再通过一次dfs求sum,然后最后dfs一次就好了

代码

#include<bits/stdc++.h>
using namespace std;
#define mem(x) memset(x,0,sizeof(x))
#define ll long long
#define A 1100000
ll head[A],nxt[A],ver[A],a[A],b[A],sum[A],f[A],dt[A];
ll tot=0,n,t,xx,yy,task;
void add(ll x,ll y){
    nxt[++tot]=head[x],head[x]=tot,ver[tot]=y;
}
void re(){
    tot=0;
    mem(head);
    mem(nxt);
    mem(ver);
    mem(sum);
    mem(dt);
    mem(b);
    mem(f);
    mem(a);
}
void dfs1(ll x,ll fa){
    sum[x]=a[x];
    for(ll i=head[x];i;i=nxt[i]){
        ll y=ver[i];
        if(y==fa) continue;
        f[y]=x;
        dfs1(y,x);
        sum[x]+=sum[y];
    }
}
void dfs0(ll x,ll fa){
    for(ll i=head[x];i;i=nxt[i]){
        ll y=ver[i];
        if(y==fa) continue;
        b[y]=b[x]+sum[1]-2*sum[y];
        dfs0(y,x);
    }
}
void work1(){
    dfs1(1,0);
    for(ll i=2;i<=n;i++){
        b[1]+=sum[i];
    }
    dfs0(1,0);
    for(ll i=1;i<=n;i++){
        printf("%lld ",b[i]);
    }
    printf("\n");
}
void dfs2(ll x,ll fa){
    for(ll i=head[x];i;i=nxt[i]){
        ll y=ver[i];
        if(y==fa) continue;
        dfs2(y,x);
//        printf("b[]=%lld %lld\n",b[y],b[x]);
        dt[y]=b[y]-b[x];
    }
}
void dfs3(ll x,ll fa){
    for(ll i=head[x];i;i=nxt[i]){
        ll y=ver[i];
        if(y==fa) continue;
        dfs3(y,x);
        sum[y]=(sum[1]-dt[y])/2;
    }
}
void dfs4(ll x,ll fa){
    a[x]=sum[x];
    for(ll i=head[x];i;i=nxt[i]){
        ll y=ver[i];
        if(y==fa) continue;
        dfs4(y,x);
        a[x]-=sum[y];
    }
}
void work2(){
    dt[1]=0;
    ll zt=0;
    dfs2(1,0);
    for(ll i=2;i<=n;i++)
        zt+=dt[i];
    sum[1]=(zt+2*b[1])/(n-1);
//    printf("sum1=%lld\n",sum[1]);
    dfs3(1,0);
    dfs4(1,0);
    for(ll i=1;i<=n;i++){
        printf("%lld ",a[i]);
    }
    printf("\n");
}
int main(){
    scanf("%lld",&t);
    while(t--){
        re();
        scanf("%lld",&n);
        for(ll i=1;i<n;i++){
            scanf("%lld%lld",&xx,&yy);
            add(xx,yy),add(yy,xx);
        }
        scanf("%lld",&task);
        task++;
        if(task==1){
            for(ll i=1;i<=n;i++){
                scanf("%lld",&a[i]);
            }
            work1();
        }
        else{
            for(ll i=1;i<=n;i++){
                scanf("%lld",&b[i]);
            }
            work2();
        }
    }
}

题

很好的一个dp？？？？

我当dp做的？？？？？

然后dp错了？？？？？？

首先对于所有的都可以列出来一个dp式子

$f[i][j][k]$表示为走了$i$步走到$j$ $k$的方案数

每一个都可以从四面八方转移过来

比如这个

　　　　f[0][0+n][0+n]=1;
        for(ll i=1;i<=n;i++){
            for(ll x=-n;x<=n;x++)
                for(ll y=-n;y<=n;y++)
                    f[i&1][x+n][y+n]=0;
            for(ll x=0;x<=n;x++)
                for(ll y=0;y<=n;y++)
                    for(ll j=1;j<=4;j++)
　　　　　　　　　　　　　　f[i&1][x+n][y+n]=(f[i&1][x+n][y+n]+f[(i-1)&1][x+nowx[j]+n][y+nowy[j]+n])%mod;

        }

然后就可以打表了

打表可以95？？？？？？

然后你优化一下就可以过掉==2的数据

　　　　else if(k==2){
        f[0][0+n][0]=1;
        f[0][0+n][1]=1;
        for(ll i=1;i<=n;i++){
            for(ll w=-n/2;w<=n/2;w++)
                f[i&1][w+n][0]=0,f[i&1][w+n][1]=0;
            for(ll x=-n/2;x<=n/2;x++)
                if(x==0)
                    f[i&1][x+n][0]=((f[i&1][x+n][0]+f[(i-1)&1][x+1+n][0]*4%mod))%mod;
                else
                    for(ll j=1;j<=2;j++)
                    f[i&1][x+n][0]=((f[i&1][x+n][0]+f[(i-1)&1][x+now[j]+n][0]))%mod;
        }
        printf("%lld\n",(f[n&1][n+0][0])%mod);
    }

打着打着发现降掉一维

    else if(k==2){
        f[0][0+n]=1;
        for(ll i=1;i<=n;i++){
            for(ll w=-n/2;w<=n/2;w++)
                f[i&1][w+n]=0;
            for(ll x=-n/2;x<=n/2;x++)
                if(x==0)
                    f[i&1][x+n]=((f[i&1][x+n]+f[(i-1)&1][x+1+n]*4%mod))%mod;
                else
                    for(ll j=1;j<=2;j++)
                    f[i&1][x+n]=((f[i&1][x+n]+f[(i-1)&1][x+now[j]+n]))%mod;
        }
        printf("%lld\n",(f[n&1][n+0])%mod);
    }

我们欢乐的过掉了==2

然后==1无脑看出Catalan

然后==3无脑Catalan相加其实可以打表