Python基础知识2-内置数据结构(下)
bytes、bytearray


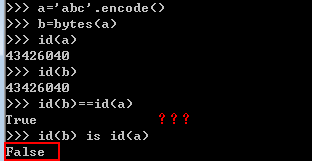
#思考下面例子:
a = 1
b = a
print(a == b)#True
print(a is b)#True
print(id(a) is id(b))#False
print(id(a) == id(b))#True
1. id():获取的是对象在内存中的地址
2. is :比对2个变量的对象引用(对象在内存中的地址,即id() 获得的值)是否相同。如果相同则返回True,否则返回False。换句话说,就是比对2个变量的对象引用是否指向同一个对象。
3. ==:比对2个变量指向的对象的内容是否相同。
参考:https://segmentfault.com/q/1010000015117621 #用id(expression a) == id(expression b)来判断两个表达式的结果是不是同一个对象的想法是有问题的
#只有你能保证对象不会被销毁的前提下,你才能用 id 来比较两个对象
print(id(a.__init__) == id(a.zhuangshi))#True
z =a.__init__
x = a.zhuangshi
print(id(z) == id(x))#False
print(id(1)is id(1))#False
print(id(1) == id(1))#False
参考:https://www.jianshu.com/p/Rvkrdb
bytes定义

bytes操作

bytearray定义

bytearray操作


线性结构

切片



练习:

#要求m行k个元素
#思路1:m行有m个元素,k不能大于m,这个需求需要保存m行的数据,那么可以使用一个嵌套机构[[],[],[]]
triangle=[]
m=5
k=4
for i in range(m):#0~4#杨辉三角每行都是以1开头
row=[1]
triangle.append(row)
if i==0:
continue
for j in range(1,i):
row.append(triangle[i-1][j-1]+triangle[i-1][j])
row.append(1)
print(triangle)
print(triangle[m-1][k-1]) #上例测试效率:

#思路2:根据杨辉三角的定理:第m行的第k个数可表示为C(m-1,k-1),即为从m-1个不同的元素中取k-1个元素的组合数。
#利用c(n,r)=n!/(r!(n-r)!)
m=9
k=5
n = m-1
r = k-1
d = n-r
targets = [] #r,n-r,n
factorial=1
for i in range(1,n+1):
factorial *=i
if i==r:
targets.append(factorial)
if i==d:
targets.append(factorial)
if i==n:
targets.append(factorial)
print(targets[2]//(targets[0]*targets[1])) #上例测试效率:

练习2

#方法1,常规写法
matrix = [[1,2,3],[4,5,6],[7,8,9]]
count = 0
for i in range(len(matrix)):
for j in range(i):#j<i
matrix[i][j]=matrix[j][i]
count+=1
print(matrix)
#方法2:利用enumerate函数创建索引
matrix = [[1,2,3],[4,5,6],[7,8,9]]
count = 0
for i,row in enumerate(matrix):
for j in enumerate(row):
if i<j:
matrix[i][j]=matrix[j][i]
count+=1
print(matrix)
练习3

#思路1:首先新建一个空的列表tm,扫描matrix第一行,在tm的第一列从上至下附加,然后在第二列附加,以此列推。
matrix = [[1,2],[3,4],[5,6]]
tm=[]
for row in matrix:
for index,col in enumerate(row):
if len(tm)<index+1:#matrix有index列就要为tm创建index行
tm.append([]) tm[index].append(col)
print(tm)
#思路2:考虑能否一次性开辟好空间目标矩阵的内存空间?如果能够一次性开辟好空间目标矩阵内存空间,那么原矩阵的元素直接移动到转置矩阵的对称坐标就行了
#在原有矩阵上改动,牵扯到增加元素和减少元素,有些麻烦,所以,定义一个新的矩阵输出
matrix = [[1,2,3],[4,5,6]]
tm=[[0 for col in range(len(matrix))]for row in range(len(matrix[0]))]
count=0
for i,row in enumerate(tm):
for j,col in enumerate(row):
tm[i][j]=tm[j][i]
count+=1
print(matrix)
print(tm)
print(count)

#考虑上面两种方法的时间效率比较:(对于大矩阵运算,方法二效率更高一些)
#测试发现,其实只要增加到4*4的矩阵,方法二的优势就开始了。
#矩阵规模越大,先开辟空间比后append的效率高!
练习4

#思路:利用类似linux中位图的思想来记录当前标记数字是否重复出现 import random nums=[]
for _ in range(10):
nums.append(random.randrange(1,21)) length=len(nums)
samenums=[] #记录相同的数字
diffnums=[] #记录不同的数字
states=[0]*length #记录不同的索引异同状态 for i in range(length):
flag = False #该状态表示没有重复
if states[i]==1:
continue
for j in range(i+1,length):#对每一个数将其与之前的数进行比较
if states[j]==1:
continue
if nums[i]==nums[j]:
flag=True
states[j]=1
if flag:
samenums.append(nums[i])
states[i]=1
else:
diffnums.append(nums[i])
print(samenums)
print(diffnums)
IPython的使用
帮助

shell命令

特殊变量

魔术方法


封装和解构


解构(unpack)


Python3的解构

丢弃变量



lst=list(range(10))
_,sec,_four,*_,2tail,_=lst

#题目1
_,(*_,a),_=lst
#题目2
s="JAVA_HOME=/usr/bin"
name,_,path=s.partition('=')
#题目3
lst = [1,9,8,5,6,7,4,3,2]
for i in range(len(lst)):
flag = False
for j in range(len(lst)-i-1):
if(lst[j+1]<lst[j]):
lst[j+1],lst[j]=lst[j],lst[j+1]
flag = True
if not flag:
break
小结:
解构,是Python提供的很好的功能,可以方便的提取复杂数据结构的值。
配合_的使用,会更加顺利。
集set

set定义初始化

初始化set的时候,里面的元素不能是可变类型,如list,bytearray等
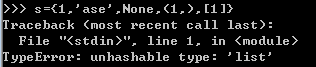
set的元素

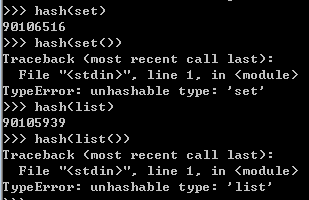
set增加

set删除

注意这里的remove是根据hash值来找到元素并移除的!所以时间复杂度是O(1).
set修改、查询

这个效率相当于用索引访问顺序结构!时间复杂度为O(1)。
set成员运算符的比较


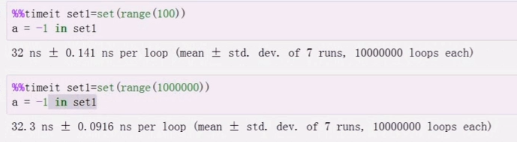
可以看出set集合查询效率跟数据规模无关!
set和线性结构

集合

集合运算
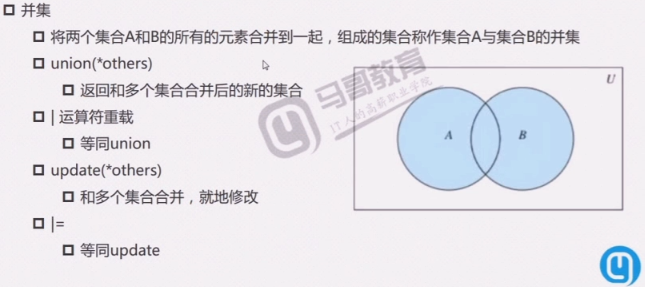








集合练习


简单选择排序

简单选择排序代码实现(一)
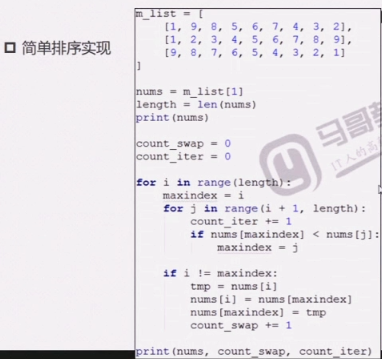
简单选择排序代码实现(二)

#二元选择排序(降序)
# lst = [9,2,1,4,5,7,6,8,3]
lst=[1,1,1,1,1,1,1]
print("原序列:",lst)
length = len(lst)
count_swap = 0
count_iter = 0 for i in range(length//2):
maxindex = i
minindex = -i-1
# minorginindex = minindex
for j in range(i+1,length-i):#!!!
count_iter += 1
if lst[maxindex]<lst[j]:
maxindex = j
count_swap += 1
if lst[minindex]>lst[-j-1]:
minindex = -j-1
count_swap += 1 if lst[minindex] == lst[maxindex]:#元素相同说明已经有序
break if i != maxindex:
lst[maxindex],lst[i] = lst[i],lst[maxindex]
#如果minindex的索引被交换过(即刚好最大值的索引和最小值的索引交换过),则需要更新!
if i == minindex+length:
minindex = maxindex if (-i-1) != minindex or (-i-1+length) != minindex:
lst[minindex], lst[-i-1] = lst[-i-1], lst[minindex]
print("排序后:",lst)
print("比较次数:{0} 交换次数:{1}".format(count_iter,count_swap))
使用二元排序的时候需要注意几点:
1.相比于(一元)简单选择排序,我们需要再添加一个变量来记录极值的下标。
2.如果两个极值的下标索引只要有一个被交换过则我们需要注意更新另一个极值的下标索引。
3.如果使用了负索引来记录下标,则在比较判断时我们需要注意索引不能为负。

简单选择排序总结

字典dict

字典dict定义初始化

#上述红色标记才是最为常用的初始化格式

字典元素的访问

字典的增加和修改

字典删除


字典遍历

Python中有序字典OrderedDict (参考:https://www.cnblogs.com/tianyiliang/p/8260741.html)


字典练习

waitting...
标准库datetime





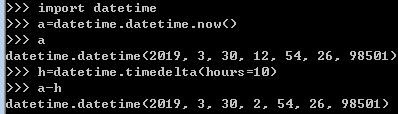

注意:total_seconds()是属于timedelta对象的方法!
标准库time

Python解析式、生成器
列表解析


注意一下下列情况:
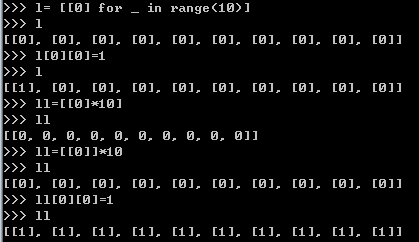



列表解析进阶




输出都是[(5,24),(6,24)]
列表解析练习

1. [x**2 for x in range(1,11)]
2. lst=[1,4,9,16,2,5,10,15]
[lst[i]+lst[i+1] for i in range(len(lst)-1)]
3. [print("{}*{}={:<3}{}".format(j,i,i*j,'\n' if i==j else ''),end='' )for i in range(1,10) for j in range(1,i+1)]
4 ["{:>04}.{}".format(i,''.join([chr(random.randint(97,123))for _ in range(10)]))for i in range(1,101)]
生成器表达式



结果会报异常:first和second都为None!

集合解析式

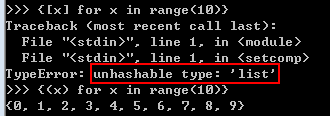
字典解析式


总结

内建函数








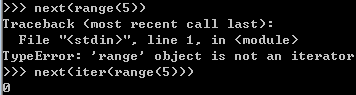
可迭代对象

迭代器

迭代器不一定是生成器,但生成器本质是迭代器!

字典练习

#按统计次数降序输出
import random
random_alphatable = [''.join([chr(random.randint(97,122))for _ in range(2)])for _ in range(1,101)]
dict_count={}
for i in random_alphatable:
if i not in dict_count:
dict_count[i] = 1
else:
dict_count[i] += 1
#即按字典的value排序
res = sorted(dict_count.items(),key=lambda items:items[1],reverse=True)
print(type(res))
for i in res:
print(i,end=" ")
Python基础知识2-内置数据结构(下)的更多相关文章
- Python的4个内置数据结构
Python提供了4个内置数据结构(内置指可以直接使用,无需先导入),可以保存任何对象集合,分别是列表.元组.字典和集合. 一.列表有序的可变对象集合. 1.列表的创建例子 list1 = []lis ...
- Python第五章-内置数据结构05-集合
Python内置数据结构 五.集合(set) python 还提供了另外一种数据类型:set. set用于包含一组无序的不重复对象.所以set中的元素有点像dict的key.这是set与 list的最 ...
- Python第五章-内置数据结构01-字符串
Python 内置的数据结构 到目前为止,我们如果想保存一些数据,只能通过变量.但是如果遇到较多的数据要保存,这个时候时候用变量就变的不太现实. 我们需要能够保存大量数据的类似变量的东东,这种 ...
- python的四种内置数据结构
对于每种编程语言一般都会规定一些容器来保存某些数据,就像java的集合和数组一样python也同样有这样的结构 而对于python他有四个这样的内置容器来存储数据,他们都是python语言的一部分可以 ...
- Python第五章-内置数据结构04-字典
Python 内置的数据结构 四.字典(dict) 字典也是 python 提供给我们的又一个非常重要且有用的数据结构. 字典在别的语言中有时叫关联数组.关联内存.Map等. 字典中存储的是一系列的k ...
- Python第五章-内置数据结构03-元组
Python 内置的数据结构 三.元组(tuple) python 作为一个发展中的语言,也提供了其他的一些数据类型. tuple也是 python 中一个标准的序列类型. 他的一些操作和str和li ...
- Python第五章-内置数据结构02-列表
Python 内置的数据结构 二.列表(list) 想一想: 前面学习的字符串可以用来存储一串信息,那么想一想,怎样存储咱们班所有同学的名字呢? 定义100个变量,每个变量存放一个学生的姓名可行吗?有 ...
- python 基础知识-day6(内置函数)
1.sorted():用于字典的排序 dict1={"name":"cch","age":"3","sex&q ...
- python面试总结4(算法与内置数据结构)
算法与内置数据结构 常用算法和数据结构 sorted dict/list/set/tuple 分析时间/空间复杂度 实现常见数据结构和算法 数据结构/算法 语言内置 内置库 线性结构 list(列表) ...
- Python的内置数据结构
Python内置数据结构一共有6类: 数字 字符串 列表 元组 字典 文件 一.数字 数字类型就没什么好说的了,大家自行理解 二.字符串 1.字符串的特性(重要): 序列化特性:字符串具有一个很重要的 ...
随机推荐
- Redis之过期时间
1.命令介绍 expire key seconds 设置key的有效时间,单位为秒expire命令返回1表示设置成功,返回0表示键不存在或设置失败. ttl keyttl命令返回值是键的剩余时间 ...
- python3 练习题 day04
'''1.整理装饰器的形成过程,背诵装饰器的固定格式''''''开放封闭原则:为了保证程序的稳定性,和功能的可开放性,在不修改目标函数源代码和调用方式的情况下,对目标函数增加新功能'''# def w ...
- 区分range() , np.arange() , np.linspace()
content: range() np.arange() np.linspace() 一.range(start, stop, step) 1.range() 为 python 自带函数 2.生成一个 ...
- PAT A1095 Cars on Campus (30 分)——排序,时序,从头遍历会超时
Zhejiang University has 8 campuses and a lot of gates. From each gate we can collect the in/out time ...
- 理论篇-MySQL知识汇总
1. 唯一索引 普通索引允许被索引的数据列包含重复的值.唯一索引则是不允许有重复的值,当然 null 除外,唯一索引不仅仅可以存储 null , 还可以存储多个 null.这么做的好处是: 简化了My ...
- [Micropython]TPYBoardV102 DIY智能温控小风扇
1.实验目的 1. 学习在PC机系统中扩展简单I/O 接口的方法. 2. 进一步学习编制数据输出程序的设计方法. 3. 学习DS18B20的接线方法,并利用DS18B20检测当前温度. 4.学习三极管 ...
- Java读写文件,字符输入流FileReader 和 字符输出流FileWriter
一个流被定义为一个数据序列.输入流用于从源文件读取数据,输出流用于向目标写数据. 字符输入流FileReader三种读文件方式 package com.shuzf.fileio; import jav ...
- 狄利克雷卷积&莫比乌斯反演总结
狄利克雷卷积&莫比乌斯反演总结 Prepare 1.\([P]\)表示当\(P\)为真时\([P]\)为\(1\),否则为\(0\). 2.\(a|b\)指\(b\)被\(a\)整除. 3.一 ...
- Linux ACL 权限
ACL 是什么 ACL的全称是 Access Control List (访问控制列表) ,一个针对文件/目录的访问控制列表.它在UGO权限管理的基础上为文件系统提供一个额外的.更灵活的权限管理机制. ...
- 【C#复习总结】垃圾回收机制(GC)1
摘要:今天我们漫谈C#中的垃圾回收机制,本文将从垃圾回收机制的原理讲起,希望对大家有所帮助. GC的前世与今生 虽然本文是以.NET作为目标来讲述GC,但是GC的概念并非才诞生不久.早在1958年,由 ...
