AVL树,红黑树

AVL树

https://baike.baidu.com/item/AVL%E6%A0%91/10986648

在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。
增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，
他们在1962年的论文《An algorithm for the organization of information》中发表了它。

红黑树

https://www.cnblogs.com/skywang12345/p/3245399.html

顺便看了一下计算机中的树...好多.高中时其实学这些最好不过了.现在...老了.

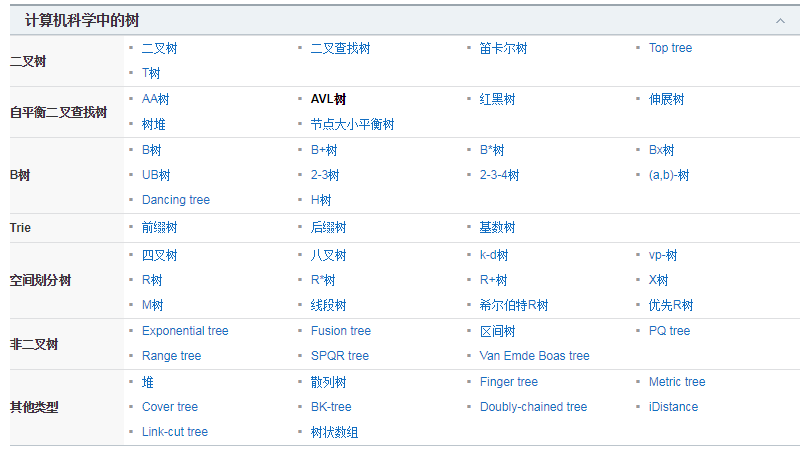
计算机科学中的树

二叉树

▪ 二叉树	▪ 二叉查找树	▪ 笛卡尔树	▪ Top tree
▪ T树

自平衡二叉查找树

▪ AA树	▪ AVL树	▪ 红黑树	▪ 伸展树
▪ 树堆	▪ 节点大小平衡树

B树

▪ B树	▪ B+树	▪ B*树	▪ Bx树
▪ UB树	▪ 2-3树	▪ 2-3-4树	▪ (a,b)-树
▪ Dancing tree	▪ H树

Trie

▪ 前缀树	▪ 后缀树	▪ 基数树

空间划分树

▪ 四叉树	▪ 八叉树	▪ k-d树	▪ vp-树
▪ R树	▪ R*树	▪ R+树	▪ X树
▪ M树	▪ 线段树	▪ 希尔伯特R树	▪ 优先R树

非二叉树

▪ Exponential tree	▪ Fusion tree	▪ 区间树	▪ PQ tree
▪ Range tree	▪ SPQR tree	▪ Van Emde Boas tree

其他类型

▪ 堆	▪ 散列树	▪ Finger tree	▪ Metric tree
▪ Cover tree	▪ BK-tree	▪ Doubly-chained tree	▪ iDistance
▪ Link-cut tree	▪ 树状数组