Logistic回归Cost函数和J(θ)的推导----Andrew Ng【machine learning】公开课

最近翻Peter Harrington的《机器学习实战》，看到Logistic回归那一章有点小的疑问。

作者在简单介绍Logistic回归的原理后，立即给出了梯度上升算法的code：从算法到代码跳跃的幅度有点大，作者本人也说了，这里略去了一个简单的数学推导。

那么其实这个过程在Andrew Ng的机器学习公开课里也有讲到。现在回忆起来，大二看Andrew的视频的时候心里是有这么一个疙瘩（Andrew也是跳过了一步推导）

这里就来讲一下作者略去了怎样的数学推导，以及，怎么推导。

在此之前，先回顾一下Logistic回归。

Logistic回归

　　基本原理：《实战》这本书上是这么讲的，“回归”就是用一条直线对一堆数据点进行拟合，这个拟合过程就称为“回归”。利用Logistic回归进行分类的主要思想是，根据现有数据对分类边界线建立回归公式，以此进行分类。

　　以Andrew公开课的例子说明：

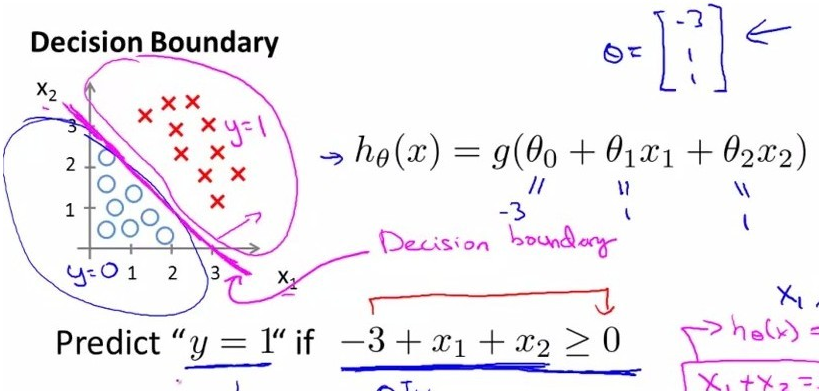
　　圆（蓝色）和叉（红色）是两类数据点，我们需要找到一个决策边界将其划分开，如图所示的边界形式显然是线性的形式，如图中所描述的：

　　我们记为：

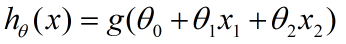
　　这里，括号里的就是决策边界的表达式，我们找一个函数g，将表达式结果作为输入，生成一个预测函数hθ(x).这里我们使用Sigmoid函数

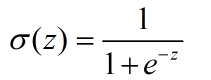
　　从而：

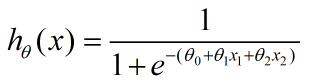
　　然而有时候，决策边界用一维直线无法区分，也就是这里的θ参数个数是变数，比如下面这堆数据

　　这是一种非线性的决策边界。

　　可以看到这里，将x1,x2参数全部平方处理，找得一个圆形边界。

　　

公式推导

　　讲到这里，我们可以把边界形式做如下推广：

　　

　　边界的最后一项是向量相乘的形式，即：

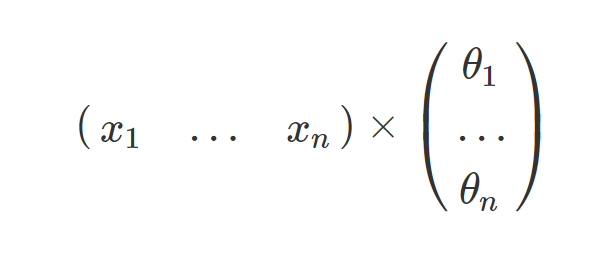
　　将其输入到sigmoid函数去判断其所属类别，就有了我们的预测函数，记为：

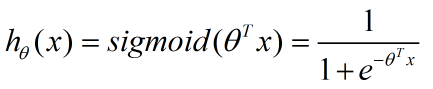
　　根据sigmoid图像，这个预测函数输出值大于0.5，那么代表x（数据点）所属类别为1，否则是0（对于二分类问题）。

　　但是别忘了我们的最初的目标，这里的θ向量未知。我们的目的是：

　　　　确定θ的参数值，使得我们这个决策边界能更好地划分数据集。

　　这个过程，在Andrew的课程里，被略过了，他直接给出了cost函数和J(θ)函数，然后通过梯度下降求得最优的θ参数。其中，J(θ)函数是这样的：

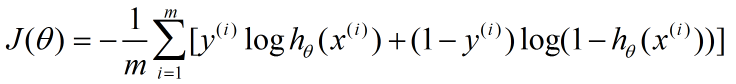
　　利用上面的公式以及梯度下降算法，我们就能求出θ的值。也就能求出最能拟合数据的决策边界。

　　接下来就要讲讲这个公式是怎么被推导出来的。

　　我们先来看看现在我们已经知道什么：

　　　　　　1、一堆数据点+它们的类别（2类）

　　　　　　2、它们的概率分布hθ(x)：虽然目前θ仍然是未知参数

　　我们的目标是求出未知参数，使得每个样本数据点属于它当前所标记的类别的概率最大。

　　于是就引出了Fisher的极大似然估计。

　　这里就不讲极大似然估计的具体概念和公式推导了，不过还是用个例子来形象的说明极大似然估计的作用吧：

　　　　　　　　一个猎人和一个学生一起走在山路上，突然从山间跑出一只兔子，啪一声枪响，兔子倒地而亡。问：谁最有可能杀死了兔子？

　　答案显而易见：猎人。那么这里，猎人就是那个参数θ。极大似然估计的目标就是预测出待估参数，使得样本事件发生的概率最大。

　　对于上述例子，用极大似然估计的思想来说明其中的几个重要信息：

样本事件	兔子被枪杀
待估参数	射死了兔子的人（记为θ：θ属于{猎人,学生}）

　　极大似然估计就是找出最有可能杀死兔子的人。

　　同样，对于本实验的一堆数据点，我们对应着看：

样本事件	每个样本数据点属于他自己的label
待估参数	决策边界参数向量θ

　　　　　　　　P.S.虽然样本里的每条数据都表明了数据点本身的类别，但是使用极大似然估计的时候，你并不知道样本本身所属的类别，样本数据自带的类别标签是你估计好坏的一个评价标准。换句话说，数据点全体就是一个样本事件

　　接下来就是估计所需要的数学推导了。

　　对于一个连续性的分布，我们需要它的概率密度函数，在本例中，其实就是那个sigmoid函数（取值范围0-1刚好表示的是发生概率），我们重新写在这里：

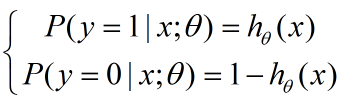
　　把这两个式子写在一起：

　　可以验证一下，当y=1或者y=0的时候，上式分别满足上上式。对每个样本数据点，满足上式，所以对于群体，我们接下来继续。

　　根据极大似然估计的求解步骤，取似然函数：

　　　　

　　要求L(θ)的最大值对应的θ参数。其中m是样本数据点的个数

　　连乘不容易求解，同时又容易造成下溢出。这里由于x和ln(x)单调性相同，两边取对数

　　这个就是Andrew给的那个J(θ)了，唯一的区别就是，Andrew在前面乘了一个负系数，使得这里求最大值变成了最小值，从而可以使用梯度下降算法。

　　不过其实用本式也可以完成任务，只是用的算法就变成梯度上升了，其实没有区别。

结语

　　这里安利一下《机器学习实战》这本书，真的蛮不错的，实践性很强，既入门了ML，又锻炼了动手能力。