对B+树，B树，红黑树的理解

出处：https://www.jianshu.com/p/86a1fd2d7406

写在前面，好像不同的教材对b树，b-树的定义不一样。我就不纠结这个到底是叫b-树还是b-树了。

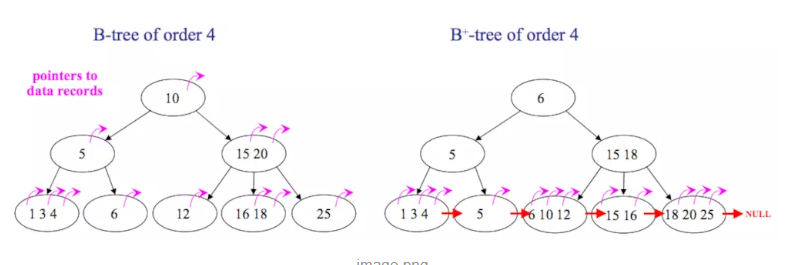
如图所示，区别有以下两点：

B+树中只有叶子节点会带有指向记录的指针，而B树则所有节点都带有，在内部节点出现的索引项不会再出现在叶子节点中。
B+树中所有叶子节点都是通过指针连接在一起，而B树不会。

B+树的优点：

非叶子节点不会带上指向记录的指针，这样，一个块中可以容纳更多的索引项，一是可以降低树的高度。二是一个内部节点可以定位更多的叶子节点。
叶子节点之间通过指针来连接，范围扫描将十分简单，而对于B树来说，则需要在叶子节点和内部节点不停的往返移动。具体的来讲，如何想扫描一次所有数据，对于b+树来说，可以从因为他们的叶子结点是连在一起的，所以可以横向的遍历过去。而对于b-树来说，就这能中序遍历了。

B树的优点：
对于在内部节点的数据，可直接得到，不必根据叶子节点来定位。

B树长什么样子？

红黑树和B树应用场景有何不同？

为什么要设计红黑树？

　　先说一下红黑树，红黑树有一个比较复杂的规则，红的结点balala怎么样，黑的结点balalal怎么样。大一大二学这些的时候，傻呵呵的想背课文一样背下来，当也不知道为什么要设计成这样。换一句话说，为什么平衡树和红黑树的区别是什么？为什么有了平衡树还要设计出来红黑树？

红黑树的规则：
1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点（叶结点即指树尾端NIL指针或NULL结点）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。
5）对于任一结点而言，其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点。

　　现在想想，我的理解是平衡树（AVL）更平衡，结构上更加直观，时间效能针对读取而言更高，但是维护起来比较麻烦！！！（插入和删除之后，都需要rebalance）。但是，红黑树通过它规则的设定，确保了插入和删除的最坏的时间复杂度是O(log N) 。

设计红黑树的目的，就是解决平衡树的维护起来比较麻烦的问题，红黑树，读取略逊于AVL，维护强于AVL，每次插入和删除的平均旋转次数应该是远小于平衡树。

小结一下：

能用平衡树的地方，就可以用红黑树。用红黑树之后，读取略逊于AVL，维护强于AVL。

红黑树和 b+树的用途有什么区别？

红黑树多用在内部排序，即全放在内存中的，STL的map和set的内部实现就是红黑树。
B+树多用于外存上时，B+也被成为一个磁盘友好的数据结构。

为什么b+磁盘友好？

磁盘读写代价更低
树的非叶子结点里面没有数据，这样索引比较小，可以放在一个blcok（或者尽可能少的blcok）里面。避免了树形结构不断的向下查找，然后磁盘不停的寻道，读数据。这样的设计，可以降低io的次数。
查询效率更加稳定
非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。
遍历所有的数据更方便
B+树只要遍历叶子节点就可以实现整棵树的遍历，而其他的树形结构要中序遍历才可以访问所有的数据。

题外话：为什么mysql索引使用b+树而不使用红黑树?

　　b+树就是为文件存储而生的。如果数据库文件存储在主存中我认为两种结构的查询速度差距不是很大，因为主存的查找速度非常快。而数据库文件实际存储在磁盘中，定位一行信息需要查找该行文件所在柱面号，磁盘号，扇区号，页号这个阶段是很耗费时间的。每一次的定位请求意味着要做一次IO操作，也意味着成倍的时间消耗。因此减少IO查询的次数是提高查询性能的关键。而IO的查询次数就是索引树的高度，高度越低查询的次数越少。同样的结点次数红黑树的高度最多为2log(n+1)，而B+树的高度最多为(logt (n+1)/2)+1,随着t增大高度会更小，IO次数也会减少。