Paper | Octave Convolution（OctConv）

目录

• 1. 尺度空间理论（scale-space theory）
• 2. OctConv
• 3. 启发

论文：Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution

1. 尺度空间理论（scale-space theory）

参考：维基百科

如果我们要处理的图像目标的大小/尺度（scale）是未知的，那么我们可以采用尺度空间理论。

其核心思想是将图像用多种尺度表示，这些表示统称为尺度空间表示（scale-space representation）。
我们对图像用一系列高斯滤波器加以平滑，而这些高斯滤波器的尺寸是不同的。
这样，我们就得到了该图像在不同尺度下的表示。

公式化：假设二维图像为\(f(x,y)\)，二维高斯函数（关于\(t\)的簇）为\(g(x,y;t) = \frac{1}{2{\pi}t}e^{-\frac{x^2+y^2}{2t}}\)，那么线性尺度空间就可以通过二者卷积（Convolution）得到：
\[
L(\cdot,\cdot;t) = g(\cdot,\cdot;t) * f(\cdot,\cdot)
\]
高斯滤波器的方差\(t = \sigma^2\)被称为尺度参数（scale parameter）。
直观地看，图像中尺度小于\(\sqrt{t}\)的结构会被平滑地无法分辨。因此，\(t\)越大，平滑越剧烈。
实际上，我们只会考虑\(t \ge 0\)的一些离散取值。当\(t = 0\)时，高斯滤波器退化为脉冲函数（impulse function），因此卷积的结果是图像本身，不作任何平滑。
看图：

事实上，我们还可以构造其他尺度空间。
但由于线性（高斯）尺度空间满足很多很好的性质，因此是使用最为广泛的。

尺度空间方法最重要的属性是尺度不变性（scale invariant），使得我们可以处理未知大小的图像目标。

最后要注意的是，在构造尺度空间时，往往还伴随着降采样。
比如\(t=2\)的尺度空间，我们会将其分辨率减半，即面积减为\(1/4\)。这也是本文的做法。

2. OctConv

作者认为：不仅自然世界中的图像存在高低频，卷积层的输出特征图以及输入通道（feature maps or channels）也都存在高、低频分量。
低频分量支撑的是整体，比如企鹅的白色大肚皮。显然，低频分量是存在冗余的，在编码过程中可以节省。

基于以上考虑，作者提出OctConv用以取代传统CNN（vanilla CNN）。有以下两个关键步骤：

第一步，我们要获得输入通道（或图像）的线性尺度表示，称为Octave feature representation。
所谓高频分量，是指不经过高斯滤波的原始通道（或图像）；
所谓低频分量，是指经过\(t=2\)的高斯滤波得到的通道（或图像）。
由于低频分量是冗余的，因此作者将低频分量的通道长/ 宽设置为高频分量通道长/ 宽的一半。
在音乐中，Octave是八音阶的意思，隔一个八音阶，频率会减半；在这里，drop an octave就是通道尺寸减半的含义。
那么高频通道和低频通道比例是多少呢？作者设置了一个超参数\(\alpha \in [0,1]\)，表示低频通道的比例。
在本文中，输入通道低频比例\(\alpha_{in}\)和输出通道低频比例\(\alpha_{out}\)设为相同。

图：企鹅白肚皮（低频）冗余（上）；传统CNN，OctConv对比（下）。

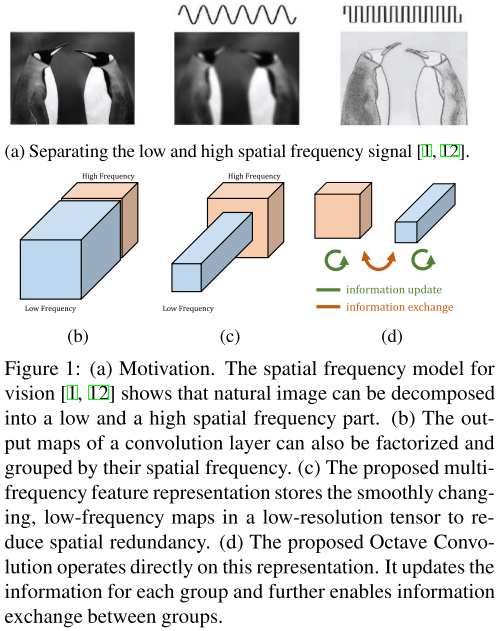
问题来了：由于高/ 低频通道尺寸不一，因此传统卷积无法执行。
但我们又不能简单地对低频通道进行升采样，因为这样不就白干了嘛，计算量和内存就没办法节省了。

因此我们有第二步：
第二步，作者提出了对应的卷积解决方案：Octave Convolution。

首先给一些定义：
设图像的低频分量和高频分量分别是\(X^L\)和\(X^H\)，卷积输出的低频分量和高频分量分别是\(Y^L\)和\(Y^H\)。卷积操作中，\(W^H\)负责构建\(Y^H\)，\(W^L\)负责构建\(Y^L\)。

我们希望：
\(W^H\)既有负责\(X^H\)到\(Y^H\)的部分：\(W^{H \to H}\)，也有负责\(X^L\)到\(Y^H\)的部分：\(W^{L \to H}\)，即\(W^H = [W^{H \to H}, W^{L \to H}]\)。

其结构如下图右边所示。
其中，\(W^{H \to H}\)是传统卷积，因为输入、输出图像尺寸一样大；对于\(W^{L \to H}\)部分，我们先对输入图像进行升采样（upsample），再执行传统卷积。这样，整体计算量仍然是减少的。
\(W^L\)同理，但对\(W^{H \to L}\)先执行的是降采样。

具体方法很简单，就是取值的问题：


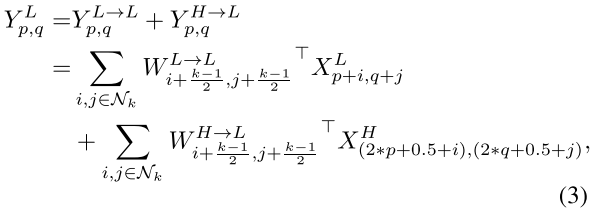
降采样后卷积相当于有步长的卷积，会不太精确；因此作者最后选择了平均池化（pooling）的方式，平均取值，采样结果会较精确一些。

完整流程如图左：

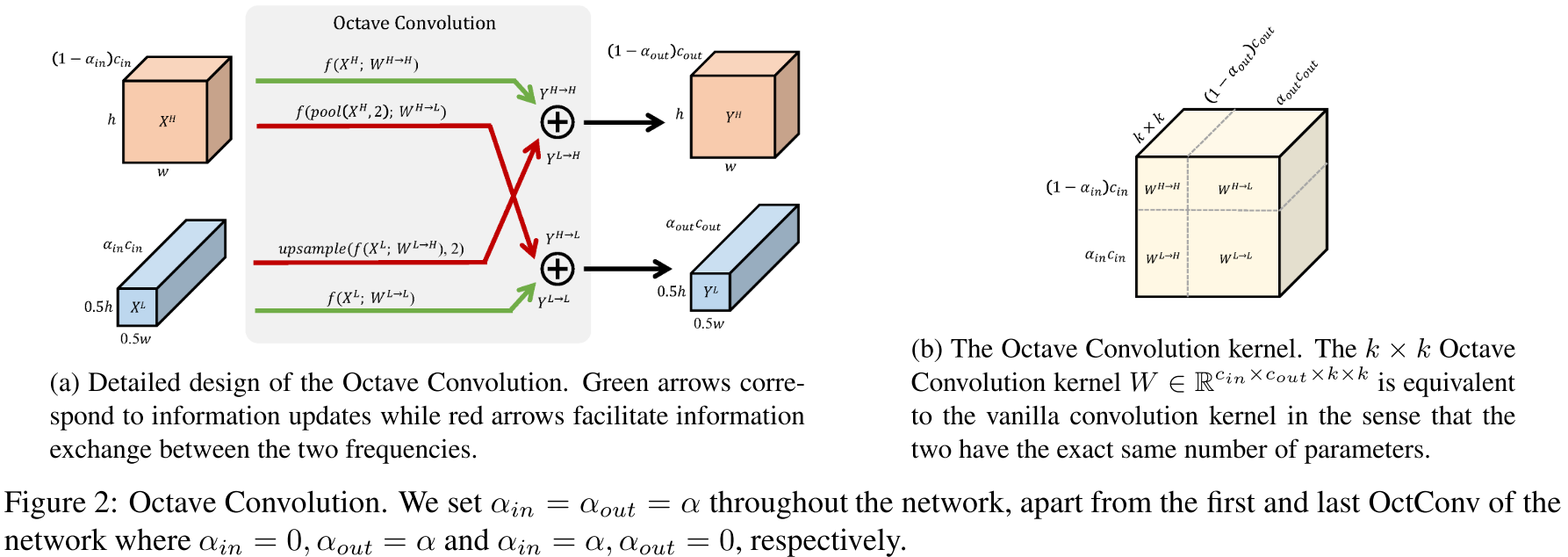
整套流程下来，我们可以发现，这种滤波+新式卷积的操作是“插片式”的，不需要破坏原来的CNN框架。
值得注意的是，低频通道卷积的感受野比传统卷积更大。
通过调整低频比例\(\alpha\)，预测精度和计算代价可以得到权衡（trade-off）。

实验效果：在算力受限的情况下（内存消耗低），图像分类的预测精度相当高。见论文。

3. 启发

1. 我们要让神经网络更好地学习。
   该文通过尺度空间变换和Octave卷积操作，让网络更清晰地分开处理高、低频分量，并且在低频分量上节约了计算量。
   又比如BN技巧，也是让网络自我学习\(\alpha\)和\(\beta\)参数，从而实现特征中心化。
   神经网络很厉害，自学能力超强，但我们要适度改造它，让它更快、更精简、更强大。

2. 我们要多从人类视觉特性上思考问题。
   因为人类视觉编码的能力远远超过现有技术：分辨率大概是10亿像素（10亿个视杆/视锥细胞），但眼睛到大脑的通路带宽只有8Mbps（1k个神经节）。
   本文思考的低频分量冗余，很有可能就是人类视觉编码特性中主要解决的冗余之一。