HDU - 6305 RMQ Similar Sequence（笛卡尔树）

http://acm.hdu.edu.cn/showproblem.php?pid=6305

题目

对于A，B两个序列，任意的l，r，如果RMQ(A，l，r)=RMQ(B，l，r)，B序列里的数为[0,1]的实数，B的重量为B的所有元素的和，否则为0。问你B的期望重量是多少。

分析

准备知识：笛卡尔树https://skywt.cn/posts/cartesian-tree/

RMQ-Similar实际上就是A和B的笛卡尔树一样。于是这个题就是笛卡尔树同构的问题，假设A的笛卡尔树的子树大小为sz[u]，那么序列B与A同构的概率为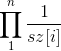，因为B中的数满足均匀分布(因为B中的元素为[0,1]中的任意实数)，所以每个位置的期望值为(0+1)/2，那么B的重量总和为n/2，所以B的重量的期望值为。

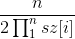实际上对这题我还没完全懂，暂且记录一下吧。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<cassert>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
typedef long long ll;
const int maxn=1e6+;
const int inf=0x3f3f3f3f;
const int mod=1e9+;

stack<int>st;
ll inv[maxn];
int n;

struct node{
    int val,sz;
    int l,r,par;
}t[maxn];

void init()
{
    for(int i=;i<=n;i++)
        t[i].l=,t[i].r=,t[i].par=,t[i].sz=;//初始化
    t[].val=inf;
    while(!st.empty())
        st.pop();
    st.push();
}

void build()
{
    for(int i=;i<=n;i++){
        while(!st.empty()&&t[st.top()].val<t[i].val)//从栈顶往栈底遍历，
            st.pop();
        int par=st.top();
        t[i].par=par;//i.par为st.pop()
        t[i].l=t[par].r;
        t[t[par].r].par=i;
        t[par].r=i;//右子树
        st.push(i);
    }
}

void dfs(int u)
{
    if(u==) return ;
    t[u].sz=;
    dfs(t[u].l);
    dfs(t[u].r);
    t[u].sz+=t[t[u].l].sz+t[t[u].r].sz;
}

void Inv(){//扩展gcd求逆元
    inv[]=;
    for(int i=;i<maxn;i++)
        inv[i]=inv[mod%i]*(mod-mod/i)%mod;
}

int main()
{
    int T;
    Inv();
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        init();
        for(int i=;i<=n;i++)
            scanf("%d",&t[i].val);
        build();
        dfs(t[].r);

        ll ans=n*inv[]%mod;
        for(int i=;i<=n;i++)
            ans=ans*inv[t[i].sz]%mod;
        printf("%lld\n",ans);
    }
}