卡尔曼滤波算法--核心公式推导导论 - ZZ

卡尔曼滤波算法--核心公式推导导论

10 个月前

写在最前面：这是我第一篇专栏文章，感谢知乎提供这么一个平台，让自己能和大家分享知识。本人会不定期的开始更新文章，文章的内容应该集中在汽车动力学控制，整车软件架构，控制器等方面。作为一名在校硕士，很多理解都可能不全面，不正确，大家有不同意见欢迎讨论。 谢谢！
---------------------------------------------------------------------------------------------------------------------------

卡尔曼滤波算法的应用很广泛，省略很多字。

卡尔曼滤波算法的优点很多，省略很多字。

卡尔曼滤波算法很牛逼，因为有一堆公式，有一堆符号，看起来就很牛逼啊，乍一看不懂的都很牛逼啊！

本文针对卡尔曼滤波算法的核心公式进行推导，不让大家被它华丽的外表吓到。（之后计划写关于针对非线性情况的EKF和UKF，对卡尔曼滤波算法做一个全面一点的应用介绍。感兴趣的可以关注专栏。）

--------------------------------------------------------------------------------------------------------------------------

Okay，进入正题。这篇文章假设读者已经对卡尔曼滤波算法有初步的了解，知道它能做什么，知道它的优点，知道它很牛逼，并且你已经对它产生兴趣，但不知道如何下手。

首先给出一个控制理论中公式，别急着翻控制理论的书，没那么复杂：

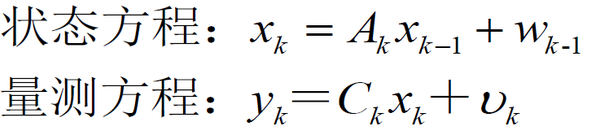两个基本问题：

1.卡尔曼滤波算法要做什么？

对状态进行估计。

2. 卡尔曼滤波算法怎么对状态进行估计？

利用状态过程噪声和测量噪声对状态进行估计。

一个状态在一个时刻点k的状态进入下一个时刻点k+1状态，会有很多外界因素的干扰，我们把干扰就叫做过程噪声，（这个词一看就是硬翻译过来的，别在意为什么叫噪声）用w表示。任何一个测量仪器，都会有误差，我们把这个误差叫做量测噪声，用v表示。

回到上面那个公式，状态方程表示状态在不断的更新，从一个时刻点进入下一个时刻点，这个很好理解。关键是量测方程，它表示，我们不断更新的状态有几个能用测量仪器测出来，比如，汽车运动状态参数有很多，比如速度，轮速，滑移率等，但是我们只能测量出轮速，因此量测方程要做的就是把状态参数中能量测的状态拿出来。

我们始终要记得我们要做的事：我们要得到的是优化的状态量Xk。

理解了上面之后就可以开始推导公式了。

1.首先不考虑过程噪声对状态进行更新，很简单：

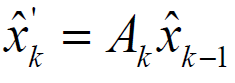举个例子，v(k)=v(k-1)+at，匀加速运动咯。

2.不考虑测量噪声取出能测量的状态，也很简单：

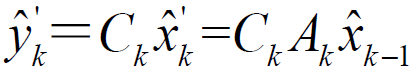3.用测量仪器测量出来的状态值（大家可以考虑到：测量的值就是被各种噪声干扰后的真实值）减去上面不考虑噪声得到的测量值：

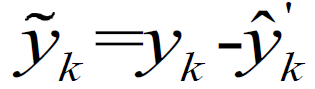这个值在数学上是一个定义值，叫做新息，有很多有趣的性质，感兴趣的可以自己谷歌。

我们对步骤暂且停一停。这个叫新息的值有什么用？由上面的过程我们可以明显看到，它反映了过程噪声和测量噪声综合对测量状态值的影响，也就是它包含了w和v的情况。

回到数学层面，（不要害怕，很简单的数学应用和思考啦！）一个数值c由两部分内容a和b组成，那么怎样用数学表达式来表达？

一般有两种做法：

I.直接相加：c=a+b;

II. 用比例的方法：a=n*c,b=(1-n)*c

卡尔曼采用了方法II，用比例的方法来做（其实这也是为什么叫做滤波的原因，因为滤波就是给权值之类的操作）。也就是说，过程噪声w=新息*一个比例。这样得到的过程噪声加上原来（第一步）不考虑过程噪声的状态值不就是优化值了吗？ 也就是：

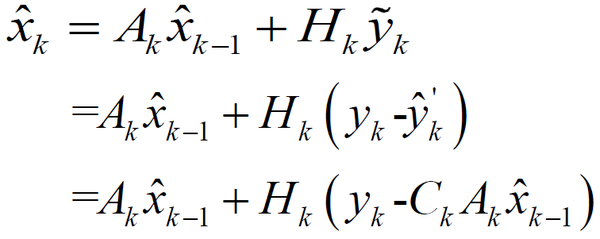Okay，都写到这里了，有必要做一下前提假设：

a. 什么高斯噪声，均值为零一堆；

b.Ak,Ck,wk的协方差Q,vk的协方差R，系统协方差初始值P0,状态初始值X0，都已知。为什么已知，你实际做项目就知道了。不过不懂的可以留言或者私信。

那么到目前为止我们的思路就是清楚了，找到一个合适的Hk值（卡尔曼增益），那么我们就能得到状态的最优值。（卡尔曼说的，不是我说的，所以你问为什么，你要问他，这么深层次的理论留给博士和学者们去做就好，我们就现学现用就行，哈哈哈，站在巨人的肩膀！）

问题来了：怎么得到合适的Hk？似乎不是随便一个参数。

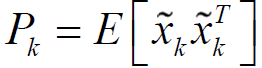这是误差协方差矩阵。

思路：使得误差协方差矩阵Pk最小的Hk。

为什么？这里我从感观的角度说明自己的理解，欢迎讨论。

协方差表示什么，协方差表示两者之间的联系或者关系，关系越大，协方差越大。误差协方差越小说明过程噪声和量测噪声的关系越小。关系越小能做什么，这要回到我们第3步讨论的我们用比例的方法分开了w和v。用比例分开，到底多少属于w，多少是v，如果关系越小，分开的越精确，比如一堆白砂糖和盐，如果两种混合的很均匀，我们说它关系很大，也就越难用比例的方法将其分开。

4.求的误差协方差矩阵Pk

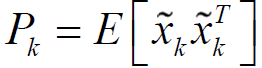自然是把里面的Xk先得到，然后公式运算，通过上面的步骤我们也容易得到：

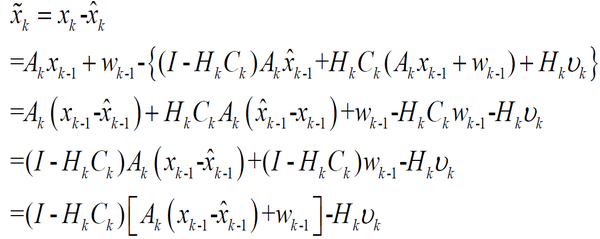然后复杂的数学计算，和之前假设的高斯噪声，新息的性质之类（至于过程，个人觉得你如果只做应用，不研究算法，就没必要深入去看了），就能得到下面的卡尔曼滤波递推公式：

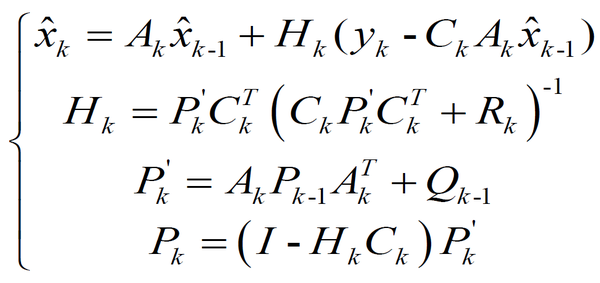通过上面的解释，我们也就不难知道这些公式都在干嘛，知道干嘛就可以了。在知道A,C,P0,Q,R的情况下，整个公式的运算流程也都很清晰了。

————————————————————————————————————————

欢迎评论！转载请注明出处！谢谢大家！