机器学习理论基础学习3.5--- Linear classification 线性分类之朴素贝叶斯

一、什么是朴素贝叶斯？

（1）思想：朴素贝叶斯假设

　　   条件独立性假设:假设在给定label y的条件下，特征之间是独立的

　　   最简单的概率图模型

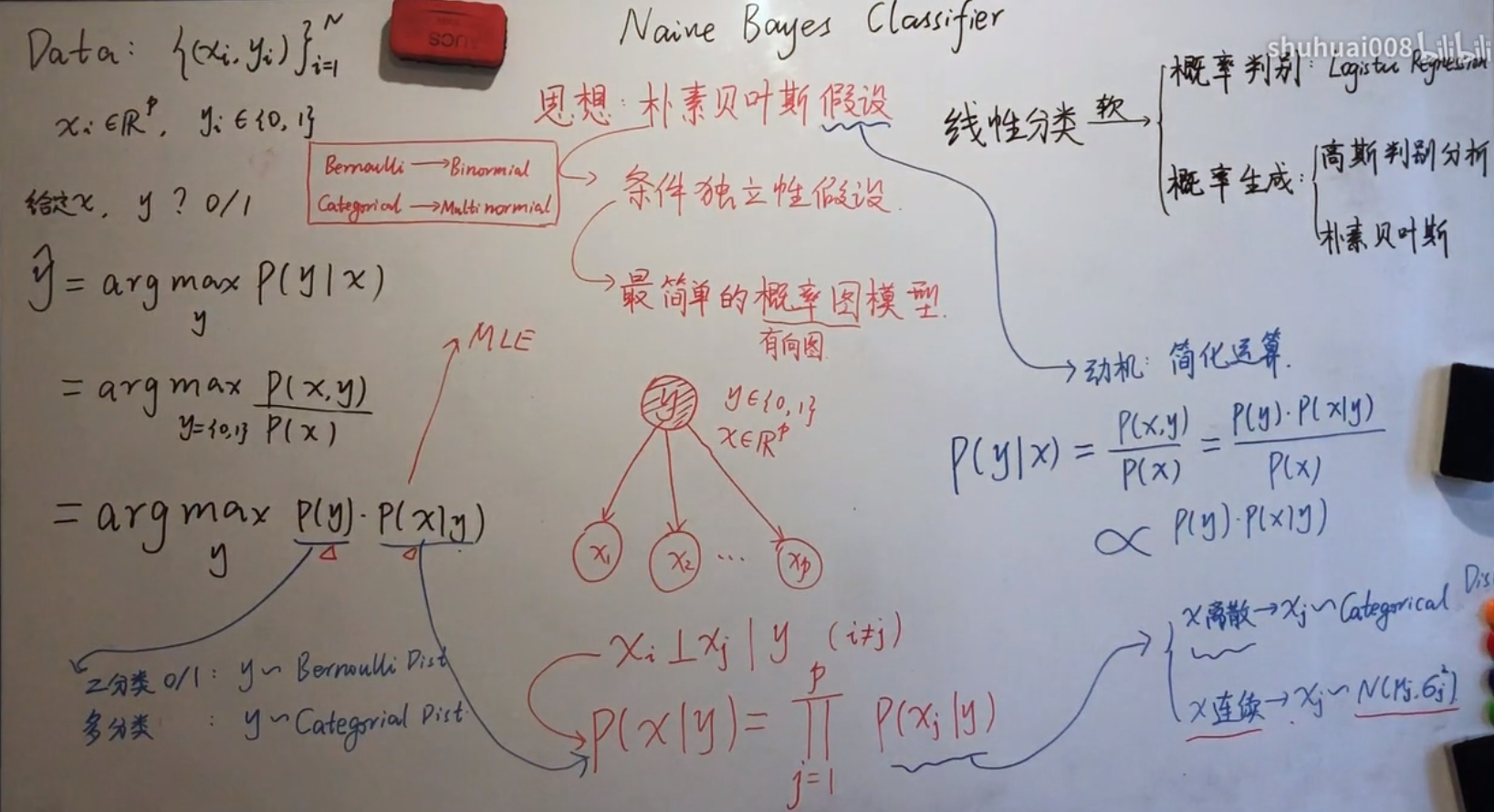
解释:

（2）重点注意：朴素贝叶斯 拉普拉斯平滑（Laplace Smoothing）

为什么要做平滑处理?

  零概率问题，就是在计算实例的概率时，如果某个量x，在观察样本库（训练集）中没有出现过，会导致整个实例的概率结果是0。在文本分类的问题中，当一个词语没有在训练样本中出现，该词语调概率为0，使用连乘计算文本出现概率时也为0。这是不合理的，不能因为一个事件没有观察到就武断的认为该事件的概率是0。

拉普拉斯的理论支撑

  为了解决零概率的问题，法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率，所以加法平滑也叫做拉普拉斯平滑。 
  假定训练样本很大时，每个分量x的计数加1造成的估计概率变化可以忽略不计，但可以方便有效的避免零概率问题。

应用举例

  假设在文本分类中，有3个类，C1、C2、C3，在指定的训练样本中，某个词语K1，在各个类中观测计数分别为0，990，10，K1的概率为0，0.99，0.01，对这三个量使用拉普拉斯平滑的计算方法如下： 
  1/1003 = 0.001，991/1003=0.988，11/1003=0.011 
  在实际的使用中也经常使用加 lambda（1≥lambda≥0）来代替简单加1。如果对N个计数都加上lambda，这时分母也要记得加上N*lambda。

二、举例

给定数据：

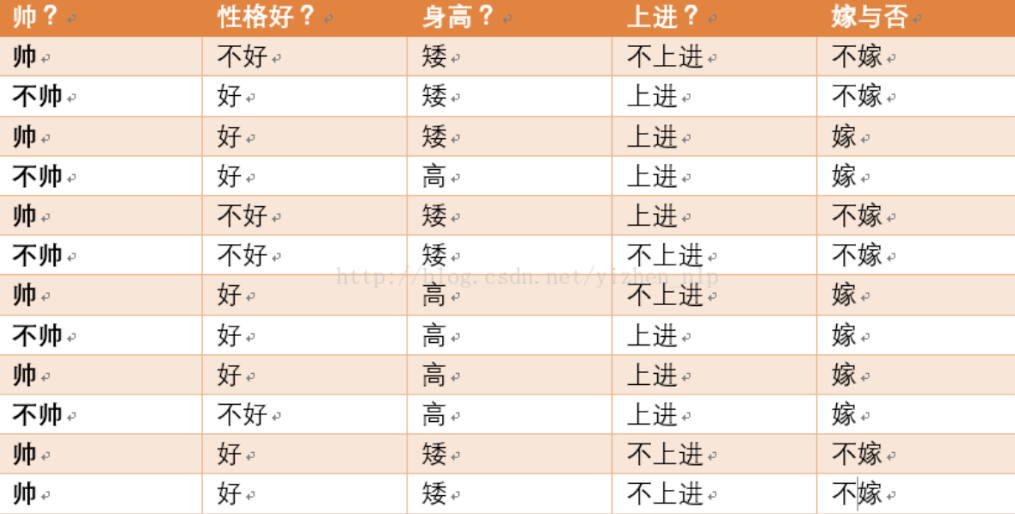
现在给我们的问题是，如果一对男女朋友，男生想女生求婚，男生的四个特点分别是不帅，性格不好，身高矮，不上进，请你判断一下女生是嫁还是不嫁？

这是典型的二分类问题，按照朴素贝叶斯的求解，转换为P(嫁|不帅、性格不好、矮、不上进)和P(不嫁|不帅、性格不好、矮、不上进)的概率，最终选择嫁与不嫁的答案。

这里我们根据贝叶斯公式:

由此，我们将(嫁|不帅、性格不好、矮、不上进)转换成三个可求的P(嫁)、P(不帅、性格不好、矮、不上进|嫁)、P(不帅、性格不好、矮、不上进)。进一步分解可以得:
P(不帅、性格不好、矮、不上进)=P(嫁)P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)+P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(矮|不嫁)P(不上进|不嫁)。
P(不帅、性格不好、矮、不上进|嫁)=P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)

将上面的公式整理一下可得:

P(嫁)=1/2、P(不帅|嫁)=1/2、P(性格不好|嫁)=1/6、P(矮|嫁)=1/6、P(不上进|嫁)=1/6。
 P(不嫁)=1/2、P(不帅|不嫁)=1/3、P(性格不好|不嫁)=1/2、P(矮|不嫁)=1、P(不上进|不嫁)=2/3
 但是由贝叶斯公式可得:对于目标求解为不同的类别，贝叶斯公式的分母总是相同的。所以，只求解分子即可：

于是，对于类别“嫁”的贝叶斯分子为：P(嫁)P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)=1/2 * 1/2 * 1/6 * 1/6 * 1/6=1/864     
对于类别“不嫁”的贝叶斯分子为:P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(矮|不嫁)P(不上进|不嫁)=1/2 * 1/3 * 1/2 * 1* 2/3=1/18。
经代入贝叶斯公式可得：P(嫁|不帅、性格不好、矮、不上进)=(1/864) / (1/864+1/18)=1/49=2.04%
P(不嫁|不帅、性格不好、矮、不上进)=(1/18) / (1/864+1/18)=48/49=97.96%
则P(不嫁|不帅、性格不好、矮、不上进) > P(嫁|不帅、性格不好、矮、不上进)，则该女子选择不嫁！

三、朴素贝叶斯的优缺点

优点：

(1）算法逻辑简单,易于实现（算法思路很简单，只要使用贝叶斯公式转化即可！）

（2）分类过程中时空开销小（假设特征相互独立，只会涉及到二维存储）

缺点：朴素贝叶斯假设属性之间相互独立，这种假设在实际过程中往往是不成立的。在属性之间相关性越大，分类误差也就越大。

四、朴素贝叶斯实战

sklearn中有三种不同类型的朴素贝叶斯问题

• 高斯分布型：用于classification问题，假定属性/特征服从正态分布的。
• 多项式型：用于离散值模型里。比如文本分类问题里面我们提到过，我们不光看词语是否在文本中出现，也得看出现次数。如果总词数为n，出现词数为m的话，有点像掷骰子n次出现m次这个词的场景。
• 伯努利型：最后得到的特征只有0(没出现)和1(出现过)。

待补充...

参考文献：

【1】带你彻彻底底搞懂朴素贝叶斯公式

【2】朴素贝叶斯算法 & 应用实例