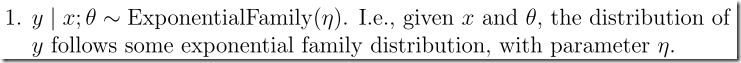【cs229-Lecture4】GLMS:选定指数分布族,如何用它来推导出GLM?
在Lecture4中有3部分内容:
- Newton’s method 牛顿方法
- Exceponential Family 指数分布族
- Generalized Linear Models 广义线性模型(GLMS)
牛顿法上一篇随便中已经讲过了,是平行于梯度下降算法的另一种最优化算法。
然后,视频中证明了伯努利分布和高斯分布都属是指数分布族中的特例的证明,实际上就是把这两种分布转化为指数分布族的形式,然后一一去对照,判断是否符合。
接下来,就讲到了当我们选定了一个指数分布族之后,如何用它来推导出一个广义线性模型(GLM),也就是本文想要讲述的内容。
首先,给出三个假设,同时我们以伯努利分布为例(01问题建模)来进行说明:
给定一个指数分布族,之前我们已经证明了伯努利分布是指数分布族的特例,因此,它满足第一个假设。
给定X,目标是求出以X为条件的T(y)的期望E[T(y)|x],即让学习算法输出h(x)=E[T(y)|x],在此处,这个期望值就等于因变量取1的概率,一般就写成P了。这个P涵盖了0-1因变量的信息,同时也能够用来比较直观地理解我们的问题:当自变量发生变化时,我们的目标变量取1的概率是怎样变化的。
假设因变量取1的概率跟自变量是线性关系。
之后会补充例子。
【cs229-Lecture4】GLMS:选定指数分布族,如何用它来推导出GLM?的更多相关文章
- 机器学习-牛顿方法&指数分布族&GLM
本节内容 牛顿方法 指数分布族 广义线性模型 之前学习了梯度下降方法,关于梯度下降(gradient descent),这里简单的回顾下[参考感知机学习部分提到的梯度下降(gradient desce ...
- Stanford大学机器学习公开课(四):牛顿法、指数分布族、广义线性模型
(一)牛顿法解最大似然估计 牛顿方法(Newton's Method)与梯度下降(Gradient Descent)方法的功能一样,都是对解空间进行搜索的方法.其基本思想如下: 对于一个函数f(x), ...
- [MCSM]Exponential family: 指数分布族
Exponential family(指数分布族)是一个经常出现的概念,但是对其定义并不是特别的清晰,今天好好看了看WIKI上的内容,有了一个大致的了解,先和大家分享下.本文基本是WIKI上部分内容的 ...
- Andrew Ng机器学习公开课笔记 -- Generalized Linear Models
网易公开课,第4课 notes,http://cs229.stanford.edu/notes/cs229-notes1.pdf 前面介绍一个线性回归问题,符合高斯分布 一个分类问题,logstic回 ...
- [读书笔记] R语言实战 (十三) 广义线性模型
广义线性模型扩展了线性模型的框架,它包含了非正态的因变量分析 广义线性模型拟合形式: $$g(\mu_\lambda) = \beta_0 + \sum_{j=1}^m\beta_jX_j$$ $g( ...
- 斯坦福CS229机器学习课程笔记 part3:广义线性模型 Greneralized Linear Models (GLMs)
指数分布族 The exponential family 因为广义线性模型是围绕指数分布族的.大多数常用分布都属于指数分布族,服从指数分布族的条件是概率分布可以写成如下形式:η 被称作自然参数(nat ...
- CS229 笔记05
CS229 笔记05 生成学习方法 判别学习方法的主要思想是假设属于不同target的样本,服从不同的分布. 例如 \(P(x|y=0) \sim {\scr N}(\mu_1,\sigma_1^2) ...
- CS229 笔记04
CS229 笔记04 Logistic Regression Newton's Method 根据之前的讨论,在Logistic Regression中的一些符号有: \[ \begin{eqnarr ...
- CS229 Lecture 01
CS229 Lecture notes 01 机器学习课程主要分为4部分:监督学习:学习理论:无监督学习:增强学习. $x^{(i)}$表示特征,$y^{(i)}$表示目标,$i=1...m$.m是训 ...
随机推荐
- CentOS 6.9编译安装Erlang
转自http://www.jb51.net/article/59823.htm 这篇文章主要介绍了CentOS 6.5源码安装Erlang教程,本文讲解了源码编译安装的过程和遇到的一些错误处理方法,需 ...
- httpclient 发送文件和字符串信息
HttpPost httpPost = new HttpPost(url); MultipartEntity reqEntity = new MultipartEntit ...
- 微软office web apps 服务器搭建之在线文档预览
案例:http://owa.linbsoft.com/op/generate.aspx# 文档地址:http://demo.linbsoft.com/CourseFile/201407/2014070 ...
- gradle 的安装
前言: 我不是一个勤奋好学的人,奔着新技术就跑去尝试学习.但是在工作或者学习的过程中,遇到了的技术,还是得一个坎一个坎的迈过去.把今天遇到的坎变成明天的垫脚石. 想学习一下 spring 的源码,然后 ...
- C# Image与Base64编码互转函数
public Bitmap GetImageFromBase64(string base64string) { byte[] b = Convert.FromBase64String(base64st ...
- man 转 pdf _____ jpg 转 pdf
man -t bash | ps2pdf - bash.pdf 将jpeg转成pdf convert *.jpeg images.pdf 将pdf转成jpeg gs -dBATCH -dNOPAUSE ...
- hbase深入了解
http://blog.csdn.net/u010967382/article/details/37878701?utm_source=tuicool&utm_medium=referral ...
- Android Material Design控件学习(三)——使用TextInputLayout实现酷市场登录效果
前言 前两次,我们学习了 Android Material Design控件学习(一)--TabLayout的用法 Android Material Design控件学习(二)--Navigation ...
- C++输入cin,输出cout,换行endl,getline连续读取字符
简记:cin=键盘,cout=屏幕. >>和<<指向代表数据流动方向.<<是流插入运算符,右操作数(运算符右边的值)会被插入到输出流中. 首先要包含:#includ ...
- scanf_s,scanf安全版本
%s,%c必须加sizeof(it)