双足步行机器人的ZMP与CoP检测

• 静态步行与动态步行

　　机器人步态分为静态步行和动态步行。当机器人做静态步行运动时，身体的各个部分运动速度很小，机器人的整体稳定性较易控制。静态步行稳定性采用机器人的重心地面投影点(Center of Gravity，简称CoG)作为稳定性标准，这种判定方法适用于运动较为缓慢的情况。如果机器人采用的是一种高速运动的步行方式，则称之为动态步行。当机器人进行动态步行时，其重心的位置和加速度的大小时刻都在变化，产生向前和侧向的惯性不容易控制，从而稳定性不好掌控。在机器人的静态步行过程中，如果重心投影的轨迹始终落在支撑面内，称之为稳定。当机器人保持静止或静态平衡时，其ZMP与重心在地面上的投影重合。当机器人步行速度较高时，由于惯性力，重心在地面上的投影点不能保证始终与ZMP重合。

• ZMP(零力矩点)和CoP(压力中心)是评价双足步行机构行走稳定性的重要参数。

　　双足步行机器人研究的一个关键问题是实现其稳定的行走。目前世界上大多数双足步行机器人系统都采用ZMP作为稳定行走的判据。ZMP是由南斯拉夫学者Vukobratovic提出的, 他研究了ZMP与双足动态系统之间的关系,提出ZMP是判断动态平衡的一个重要依据。ZMP是地面上的一点，重力和惯性力对这一点的力矩，其水平分量为零。即整个系统对于这个点的前向、侧向的倾覆力矩为零。他指出，当双足机构处于动态平衡时,ZMP和脚底所受地面反力的压力中心CoP是重合的。因此,我们可以根据检测到的地面反力信息,计算CoP,通过控制策略调整ZMP和CoP的位置,使二者重合,实现机器人的动态稳定行走。日本本田公司的机器人ASIMO通过安装在脚部的六维力/力矩传感器检测出地面反力信息, 计算得到CoP,通过独特的姿态控制同时调整躯干姿态和脚部姿态, 进而保持ZMP和CoP 在行走过程中始终处于合适的位置, 实现稳的行走。

　　对于处于动态平衡下的双足机器人, 在单脚支撑期间内, ZMP与CoP是重合的。对于单脚支撑期的动态不平衡状态, 整个机器人机构围绕脚的边缘发生旋转或翻转, ZMP和CoP是不重合的。根据定义可知CoP是永远不会离开支撑区域的, 而ZMP可以离开支撑区域。（If the robot is dynamically stable ,ZMP coincides with CoP and can be calculated with CoP by using force sensors on the foot. If the biped is not dynamically stable ,the CoP can still be determined but this location does not represent the ZMP）。ZMP点由于计算比较容易，常用于行走步态的生成，而CoP则由于容易直接测量，更适合用于对机器人行走进行控制。ZMP作为机器人稳定行走的一个充分条件，使用范围有一定的限制：当足底打滑、地面不平、或者机器人上身与外界环境接触时，ZMP就不能应用。

　　当ZMP处于支撑区域之外时, 机器人就会倾倒。作用在机器人脚底的实际地面反力(包括垂直反力和摩擦力)作用点如能与期望ZMP重合，并落在支撑多边形内,则对于机器人无翻转力矩，处于稳定行走状态。期望ZMP可通过实际结构尺寸、重量、步态规划进行计算。实际ZMP需要由六维力/力矩传感器（或多个压力传感器）进行测量，传感器的最佳安装位置应在踝关节以下，越接近地面越好。

• 支撑多边形

　　支撑多边形是指机器人足底面和地面接触点构成的最小多边形；对于单腿支撑, 根据定义其支撑多边形就是支撑腿的足底接触面;对于双腿支撑可分两种情况, 一种为两腿都完全与地面接触（图2）, 另一种是其中一条腿即将离地时（图3）。由图2 可知, 两腿足底完全接触地面时的支撑面为多边形ABCDEF , 当其中一腿即将离地时, 它的接触面变成一条线, 支撑面也会变成多边形ABDEF。根据支撑多边形和零力矩点ZMP的定义, 可得到零力矩点始终落在支撑多边形内而不能落到边缘之外, 这为机器人是否稳定行走提供了判断的依据, 即利用传感器检测ZMP的位置与支撑多边形边界进行比较判断行走是否趋于稳定;在一般情况下, 为了预先防止ZMP 坐落在支撑多边形边界上这一情况的发生, 通常距支撑多边形边界留出一段距离作为稳定裕度。

• ZMP测量

　　通过安装在足底的压力传感器测量各个离散点的压力,离散点的数量越多，ZMP的估计越准确。

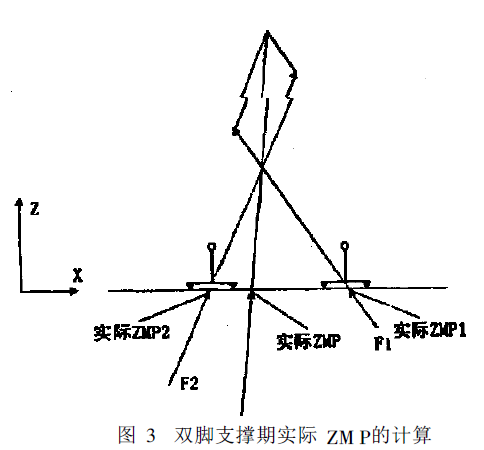
　　以上为单脚支撑期的实际ZMP的计算公式。在双足步行机器人的行走过程中，还有双脚支撑期。当机器人处于双脚支撑期时，每只脚的实际ZMP仍然用以上公式计算，整个机器人系统的实际ZMP可按下式计算，推导过程可参照图3所示。式子中X1、X2、Y1、Y2分别为左右脚ZMP点在参考坐标系中的坐标。F_z1、F_z2分别为左右脚4个压力传感器计算出的竖直方向的合力。

• ZMP计算

　　对于研究机器人步行运动，通常都是计算ZMP运动轨迹来反映步行的稳定性。通过重力与惯性力的合力来定义ZMP的坐标计算公式，并用达朗贝尔原理进行推导。(推导时注意坐标轴以及力/力矩的方向)

　　设机器人各个连杆质量为m_i，连杆质心坐标为(x_i,y_i,z_i)，重力和惯性力的合力为：

　　该合力对各个坐标轴的矩为：

　　将合力从参考坐标系原点移动到ZMP点，ZMP点处合力矩对X,Y轴分量为零，则有：

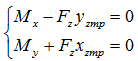
　　可求得：

　　不考虑惯性力的影响，则上式变为：

　　忽略惯性力的影响后，ZMP与CoG（重心在地面上的投影）重合。由此可见，静态步行为动态步行的特例。

参考：

　　1. 刘莉，汪劲松，陈恳，杨东超，赵建东. 基于六维力/力矩传感器的拟人机器人实际ZMP检测[J]. 机器人. 第23卷第5期，2001年9月

　　2. 常江. 基于ZMP 的双足机器人稳定性分析[J]. 佳木斯大学学报( 自然科学版). 第27卷第1期，2009年01月

　　3. 林玎玎, 刘莉, 赵建东, 陈恳. 双足步行机器人的ZMP-CoP检测及研究[J]. 机器人. 第26卷第4期,2004年7月