Fisher线性判别分析

1、概述

在使用统计方法处理模式识别问题时，往往是在低维空间展开研究，然而实际中数据往往是高维的，基于统计的方法往往很难求解，因此降维成了解决问题的突破口。

假设数据存在于d维空间中，在数学上，通过投影使数据映射到一条直线上，即维度从d维变为1维，这是容易实现的，但是即使数据在d维空间按集群形式紧凑分布，在某些1维空间上也会难以区分，为了使得数据在1维空间也变得容易区分，需要找到适当的直线方向，使数据映射在该直线上，各类样本集群交互较少。如何找到这条直线，或者说如何找到该直线方向，这是Fisher线性判别需要解决的问题。

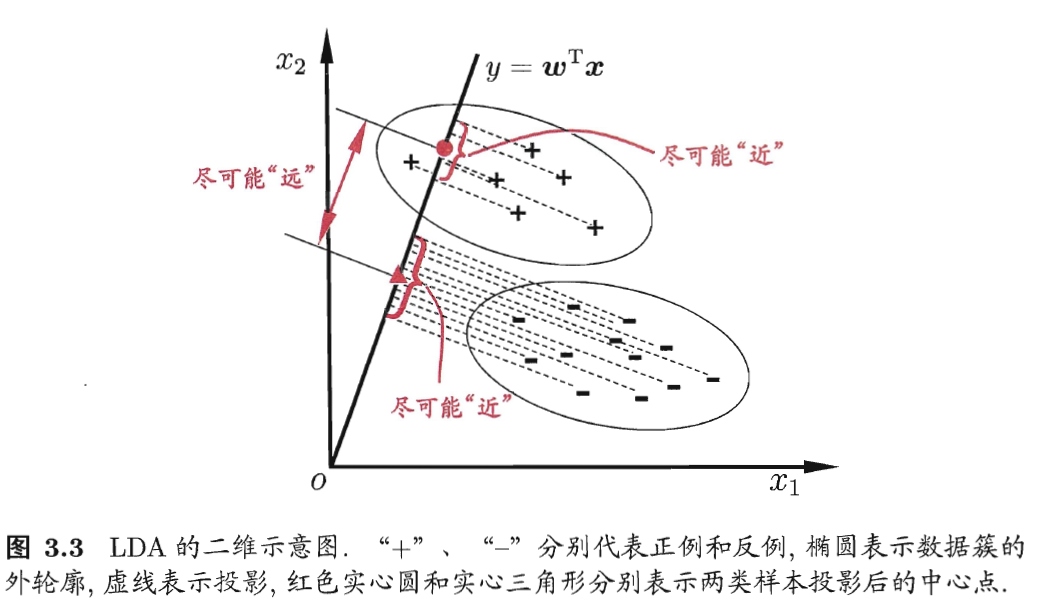
2、从d维空间变换到1维空间

3、介绍几个基本的参量

A. 在d维原始空间

B. 在1维映射空间

4、Fisher准则函数

5、学习算法推导

6、决策分类

Fisher线性判别分析的更多相关文章

  1. 线性判别分析（LDA）准则：FIsher准则、感知机准则、最小二乘（最小均方误差）准则

    准则 采用一种分类形式后,就要采用准则来衡量分类的效果,最好的结果一般出现在准则函数的极值点上,因此将分类器的设计问题转化为求准则函数极值问题,即求准则函数的参数,如线性分类器中的权值向量. 分类器设 ...

  2. 线性判别分析（Linear Discriminant Analysis）转载

    1. 问题 之前我们讨论的PCA.ICA也好,对样本数据来言,可以是没有类别标签y的.回想我们做回归时,如果特征太多,那么会产生不相关特征引入.过度拟合等问题.我们可以使用PCA来降维,但PCA没有将 ...

  3. 线性判别分析算法（LDA）

    1. 问题 之前我们讨论的PCA.ICA也好,对样本数据来言,可以是没有类别标签y的.回想我们做回归时,如果特征太多,那么会产生不相关特征引入.过度拟合等问题.我们可以使用PCA来降维,但PCA没有将 ...

  4. （数据科学学习手札17）线性判别分析的原理简介&Python与R实现

    之前数篇博客我们比较了几种具有代表性的聚类算法,但现实工作中,最多的问题是分类与定性预测,即通过基于已标注类型的数据的各显著特征值,通过大量样本训练出的模型,来对新出现的样本进行分类,这也是机器学习中 ...

  5. LDA(Linear discriminate analysis)线性判别分析

    LDA 线性判别分析与Fisher算法完全不同 LDA是基于最小错误贝叶斯决策规则的. 在EMG肌电信号分析中,... 未完待续:.....

  6. 线性判别分析（LDA）, 主成分分析(PCA)及其推导【转】

    前言: 如果学习分类算法,最好从线性的入手,线性分类器最简单的就是LDA,它可以看做是简化版的SVM,如果想理解SVM这种分类器,那理解LDA就是很有必要的了. 谈到LDA,就不得不谈谈PCA,PCA ...

  7. 机器学习中的数学-线性判别分析（LDA）, 主成分分析(PCA)

    转:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html 版权声明: 本文由L ...

  8. 机器学习中的数学(4)-线性判别分析（LDA）, 主成分分析(PCA)

    版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gm ...

  9. LDA 线性判别分析

    LDA, Linear Discriminant Analysis,线性判别分析.注意与LDA(Latent Dirichlet Allocation,主题生成模型)的区别. 1.引入 上文介绍的PC ...

随机推荐

  1. 在Win7系统下， 使用VS2015 打开带有日文注释程序出现乱码的解决方案

    在Win7系统下, 使用VS2015 打开带有日文注释程序出现乱码的解决方案 下载: apploc.msi (下载地址:http://microsoft-applocale.software.info ...

  2. recv函数返回值说明

    recv函数 int recv( SOCKET s, char FAR *buf, int len, int flags); 不论是客户还是服务器应用程序都用recv函数从TCP连接的另一端接收数据. ...

  3. mybitis学习笔记

    <?xml version="1.0" encoding="UTF-8" ?><!DOCTYPE mapperPUBLIC "-// ...

  4. tfs项目解绑及svn上传

    1.tfs解绑 file--源代码管理——tfs解绑 2.svn将本地的文件夹上传到server 右击--import--url--新建文件夹

  5. Ajax—web中ajax的常用方式

    什么Web2.0的特点? 1:注重用户贡献度 2:内容聚合RSS协议(每小块都个性化,单独加载单独请求,不用全部刷新--Ajax) 3:更丰富的用户体验 Ajax的概念? "Asynchro ...

  6. 文件操作(CRT、C++、WIN API、MFC)

    一.使用CRT函数文件操作 二.使用标准C++库 std::fstream std::string 1)std::string对象内部存储了一个C的字符串,以'\0'结尾的. 2)std::strin ...

  7. VNC的安装和常用命令

    主要参考文章:http://www.cnblogs.com/coderzh/archive/2008/07/16/1243990.html                         http:/ ...

  8. Ubuntu系统下Jenkins的git构建基本方法

    上一博文讲到了本地脚本的构建方法. 本篇博文主要讲“Ubuntu系统下Jenkins的git构建基本方法”. 点击保存后即可完成简单的构建. 构建触发器 这个触发器是决定什么时候触发构建,可以设置为定 ...

  9. SNMP学习笔记之SNMPv3的配置和认证以及TroubleShooting

    0x00 增加snmp v3用户 增加用户的时候,必须要停止SNMP服务. # service snmpd stop # net-snmp-config --create-snmpv3-user -r ...

  10. c++性能之map实现性能比较

    http://www.cnblogs.com/zhjh256/p/6346501.html讲述了基本的map操作,在测试的时候,发现map的性能极为低下,与java相比相差了接近200倍.测试的逻辑如 ...