AVLMap平衡二叉树

public class AVLMap<K, V> implements Iterable<AVLEntry<K, V>> {
    private int size;
    private AVLEntry<K, V> root;
    private Comparator<K> comp;
    private LinkedList<AVLEntry<K, V>> stack = new LinkedList<AVLEntry<K, V>>();

    private int compare(K a, K b) {
        if (comp != null) {
            return comp.compare(a, b);//有比较器就用比较器比较
        } else {
            Comparable<K> c = (Comparable<K>) a;
            return c.compareTo(b);//没有比较器就用对象本身比较
        }
    }

    public AVLMap(Comparator<K> comp) {
        super();
        this.comp = comp;
    }

    public AVLMap() {
        super();
    }

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0 ? true : false;
    }

    public V put(K key, V value) {//存放节点，并把相比较过了的节点加入到stack。
        if (root == null) {//第一个元素是根
            root = new AVLEntry<K, V>(key, value);
            stack.push(root);
            size++;
        } else {
            AVLEntry<K, V> p = root;//每次从根节点开始比较，stack存放依次比较路上的所有节点，
            while (p != null) {
                stack.push(p); //调整二叉树时候用
                int compareResult = compare(key, p.key);//-1:<，key<p.key
                if (compareResult == 0) {
                    p.setValue(value);//相等就覆盖
                    break;
                } else if (compareResult < 0) {//小于0就跟左节点比较，左节点入栈，
                    if (p.left == null) {
                        p.left = new AVLEntry<K, V>(key, value);
                        System.out.println(p.left);
                        size++;
                        stack.push(p.left);//刚刚加入的节点也入栈
                        break;
                    } else {// 还有左子树
                        p = p.left;
                    }
                } else {
                    if (p.right == null) {//大于0就跟右节点比较，右节点入栈，
                        p.right = new AVLEntry<K, V>(key, value);
                        size++;
                        stack.push(p.right);//刚刚加入的节点也入栈
                        break;
                    } else {// 还有右子树
                        p = p.right;
                    }
                }
            }
        }
        fixAfterInsertion(key);//修改依次比较路上的所有节点的高度，
        return value;
    }

    @Override
    public Iterator<AVLEntry<K, V>> iterator() {
        return new AVLIterator<K, V>(root);
    }

    private AVLEntry<K, V> getEntry(K key) {
        AVLEntry<K, V> p = root;
        while (p != null) {
            int compareResult = compare(key, p.key);
            if (compareResult == 0) {
                return p;
            } else if (compareResult < 0) {
                p = p.left;
            } else {
                p = p.right;
            }
        }
        return null;
    }

    public boolean containsKey(K key) {
        AVLEntry<K, V> p = getEntry(key);
        return p != null;
    }

    public V get(K key) {
        AVLEntry<K, V> p = getEntry(key);
        return p != null ? p.getValue() : null;
    }

    public boolean containsValue(V value) {
        Iterator<AVLEntry<K, V>> itr = this.iterator();
        while (itr.hasNext()) {
            if (itr.next().getValue().equals(value)) {
                return true;
            }
        }
        return false;
    }

    public AVLEntry<K, V> getFirstEntry(AVLEntry<K, V> p) {
        if (p == null) {
            return null;
        }
        while (p.left != null) {
            p = p.left;
        }
        return p;
    }

    public AVLEntry<K, V> getLastEntry(AVLEntry<K, V> p) {
        if (p == null) {
            return null;
        }
        while (p.right != null) {
            p = p.right;
        }
        return p;
    }

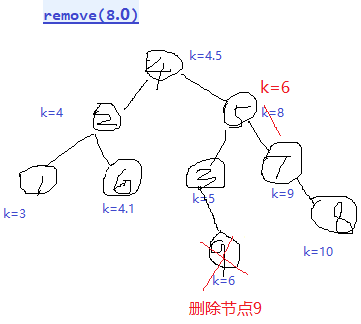
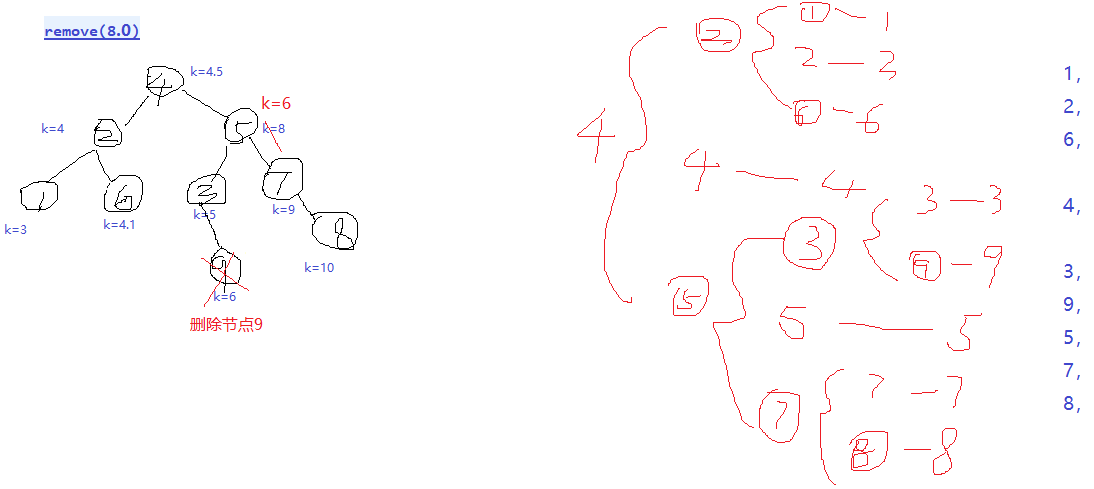
    private AVLEntry<K, V> deleteEntry(AVLEntry<K, V> p, K key) {//从根节点开始删除，
        if (p == null) {
            return null;
        } else {
            int compareResult = compare(key, p.key);
            if (compareResult == 0) {//删除就是p节点，不是删除p节点，而是修改p节点，删除的是被替换的节点。
                if (p.left == null && p.right == null) {
                    p = null;
                } else if (p.left != null && p.right == null) {
                    p = p.left;
                } else if (p.left == null && p.right != null) {
                    p = p.right;
                } else {//从右边和从左边开始是一样的。
                    if ((size & 1) == 0) {//偶数
                        AVLEntry<K, V> rightMin = getFirstEntry(p.right);//p.right最左边的节点，就是比p大但是最小的。
                        p.key = rightMin.key;
                        p.value = rightMin.value;//修改要删除节点p的k，v，
                        AVLEntry<K, V> newRight = deleteEntry(p.right, p.key);//从p.right开始删除p.key
                        p.right = newRight;//修改要删除节点p的right,
                    } else {//奇数
                        AVLEntry<K, V> leftMax = getLastEntry(p.left);//p.left最右的节点，就是小于p但是最大的，
                        p.key = leftMax.key;
                        p.value = leftMax.value;
                        AVLEntry<K, V> newLeft = deleteEntry(p.left, p.key);//从p.left开始删除p.key
                        p.left = newLeft;
                    }
                }
            } else if (compareResult < 0) {
                AVLEntry<K, V> newLeft = deleteEntry(p.left, key);//从p.left开始删除，返回并修改新的顶点p.left
                p.left = newLeft;
            } else {
                AVLEntry<K, V> newRight = deleteEntry(p.right, key);//从p.right开始删除，返回并修改新的顶点p.right
                p.right = newRight;
            }
            p = fixAfterDeletion(p);
            return p;//返回的是根节点
        }
    }

    public int getHeight(AVLEntry<K, V> p) {
        return p == null ? 0 : p.height;//p==null?0:Max(getHeight(p.left),getHeight(p.right))+1
    }

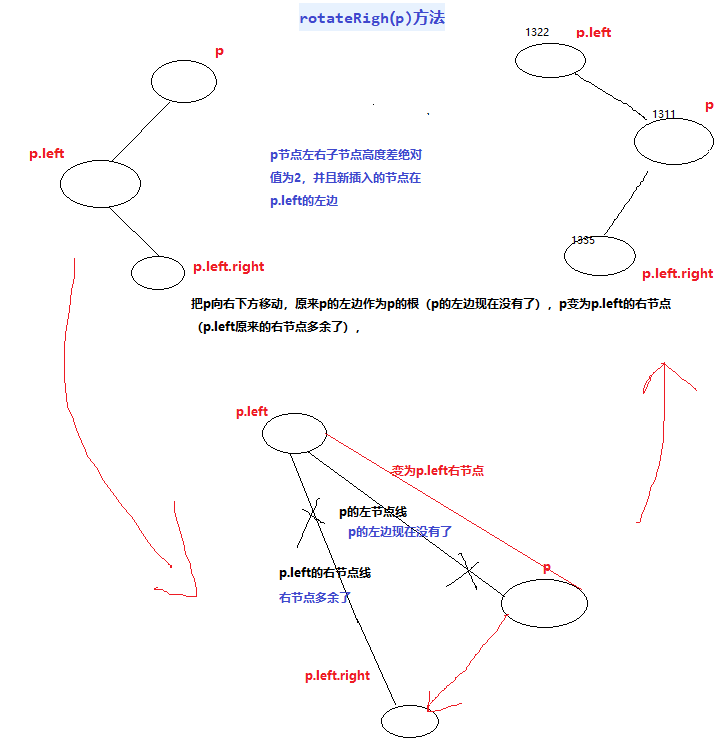
    private AVLEntry<K, V> rotateRight(AVLEntry<K, V> p) {//向右旋转，返回现在的顶节点p.left
        AVLEntry<K, V> left = p.left;
        p.left = left.right;
        left.right = p;
        p.height = Math.max(getHeight(p.left), getHeight(p.right)) + 1;//重新计算高度
        left.height = Math.max(getHeight(left.left), p.height) + 1;//重新计算高度
        return left;
    }

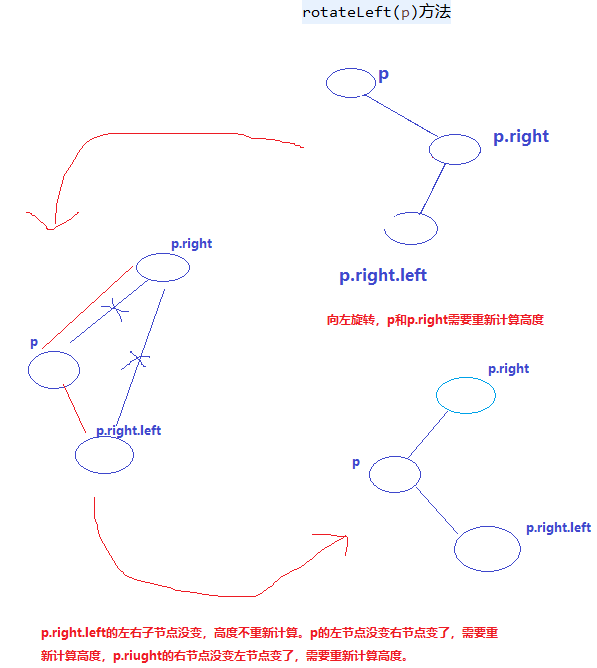
    private AVLEntry<K, V> rotateLeft(AVLEntry<K, V> p) {//向左旋转，返回现在的顶节点p.right
        AVLEntry<K, V> right = p.right;
        p.right = right.left;
        right.left = p;
        p.height = Math.max(getHeight(p.left), getHeight(p.right)) + 1;//重新计算高度
        right.height = Math.max(p.height, getHeight(right.right)) + 1;//重新计算高度
        return right;
    }

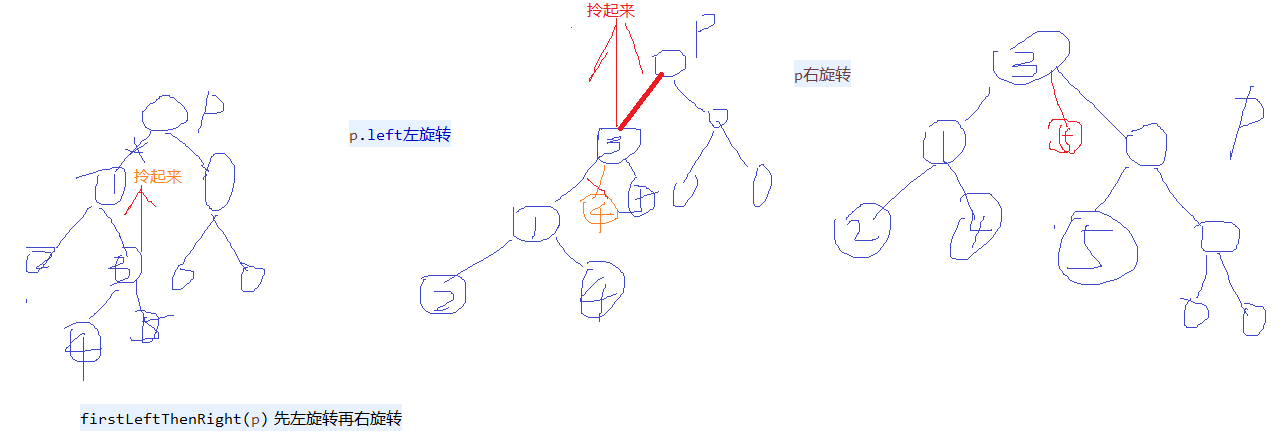
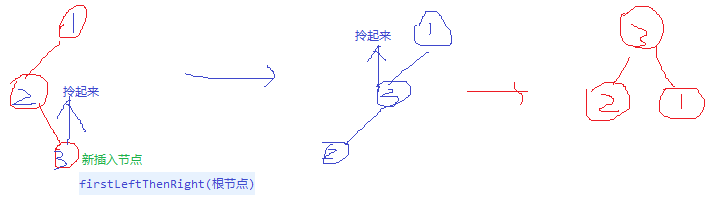
    private AVLEntry<K, V> firstLeftThenRight(AVLEntry<K, V> p) {
        p.left = rotateLeft(p.left);//p.left.right为p.left
        p = rotateRight(p);
        return p;
    }

    private AVLEntry<K, V> firstRightThenLeft(AVLEntry<K, V> p) {
        p.right = rotateRight(p.right);
        p = rotateLeft(p);
        return p;
    }
    //一路上比较的节点都要重新调整大小，因为新加进去的节点在这些节点的下面，所以这些节点都要重新调整高度。
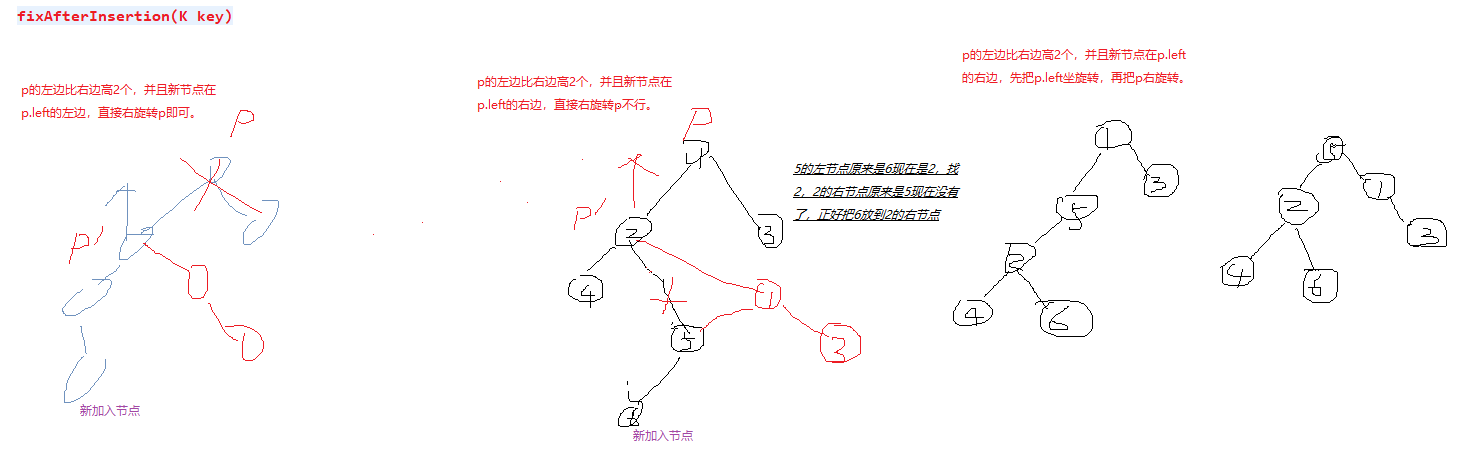
    private void fixAfterInsertion(K key) {//从新插入的节点到根节点，依次修改比较路上的节点的高度，
        AVLEntry<K, V> p = root;//根
        while (!stack.isEmpty()) {
            p = stack.pop();//比较路上的所有节点，包括刚刚加进去的节点，第一次pop出来的是最外面的节点，
            //就是刚刚加进去的节点，高度是1，然后依次修改比较路上的节点的高度。不在比较路上的节点的高度不要修改。
            int newHeight = Math.max(getHeight(p.left), getHeight(p.right)) + 1;
            if (p.height > 1 && newHeight == p.height) {//节点p的高度没改变
                stack.clear();//那么p的上层节点高度也没改变
                return;
            }
            p.height = newHeight;//修改高度
            int d = getHeight(p.left) - getHeight(p.right);
            if (Math.abs(d) <= 1) {//绝对值
                continue;
            } else {//左右子树高度差>=2,每次只增加一个节点，所以高度差从2开始，不会大于2，等于2就开始旋转调整。
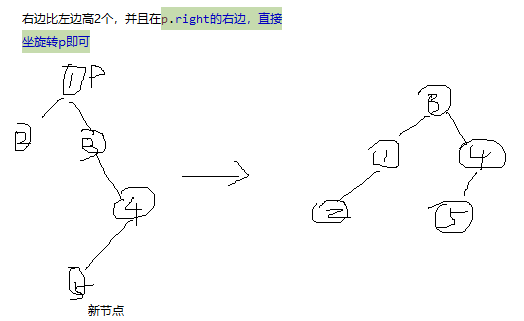
                if (d == 2) {//p左边比右边高2个，
                    //新插入的节点在p.left的左边，直接p右旋转，
                    if (compare(key, p.left.key) < 0) {
                        p = rotateRight(p);//返回现在的顶节点
                    } else {//新插入的节点在p.left的右边，先把p.left左旋转，
                        p = firstLeftThenRight(p);
                    }
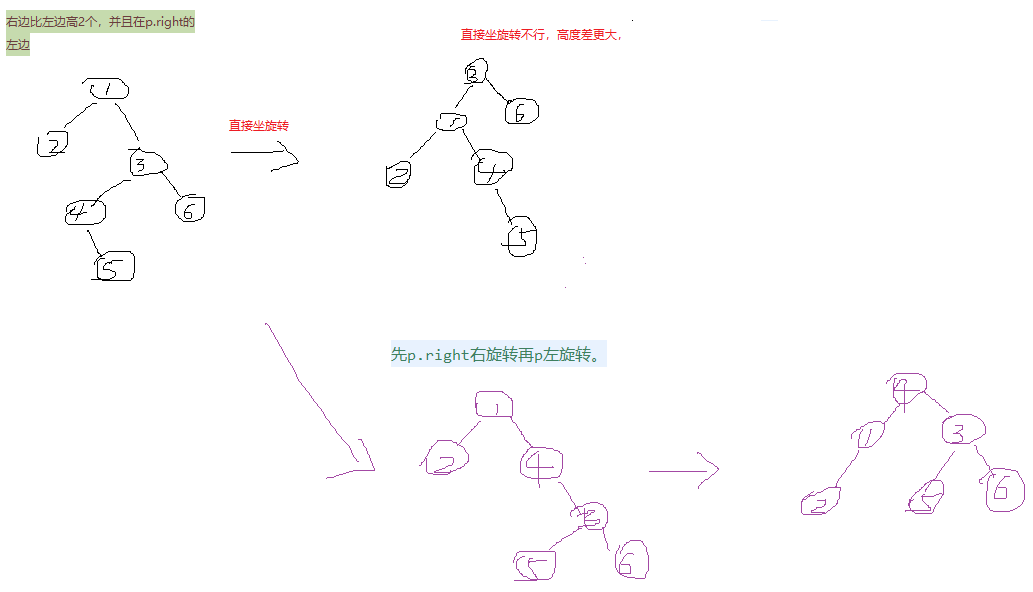
                } else {//-2,p右边比左边高2个，
                    if (compare(key, p.right.key) > 0) {//p.right的右边直接左旋转即可。
                        p = rotateLeft(p);//返回现在的顶节点
                    } else {//先p.right右旋转再p左旋转。
                        p = firstRightThenLeft(p);
                    }
                }
                if (!stack.isEmpty()) {//peek()不移除元素
                    if (compare(key, stack.peek().key) < 0) {//表示在节点stack.peek()的左边
                        stack.peek().left = p;//就设置左边
                    } else {
                        stack.peek().right = p;
                    }
                }
            }
        }
        root = p;//修改根节点
    }

    public void checkBalance() {//断言AVL树的平衡性
        postOrderCheckBalance(root);
    }

    private void postOrderCheckBalance(AVLEntry<K, V> p) {
        if (p != null) {
            postOrderCheckBalance(p.left);
            postOrderCheckBalance(p.right);
            Assert.assertTrue(Math.abs(getHeight(p.left) - getHeight(p.right)) <= 1);
        }
    }

    public V remove(K key) {
        AVLEntry<K, V> entry = getEntry(key);
        if (entry == null) {
            return null;
        }
        V oldValue = entry.getValue();
        root = deleteEntry(root, key);//从根节点开始删除。删除路上的所有节点都要重新调整为平衡二叉树。
        size--;
        return oldValue;
    }

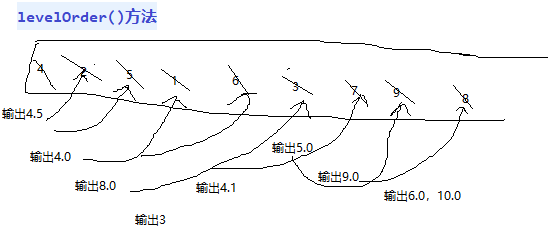
    public void levelOrder() {
        Queue<AVLEntry<K, V>> queue = new LinkedList<AVLEntry<K, V>>();
        queue.offer(root);
        int preCount = 1;
        int pCount = 0;
        while (!queue.isEmpty()) {
            preCount--;
            AVLEntry<K, V> p = queue.poll();
            System.out.print(p + " ");
            if (p.left != null) {
                queue.offer(p.left);
                pCount++;
            }
            if (p.right != null) {
                queue.offer(p.right);
                pCount++;
            }
            if (preCount == 0) {
                preCount = pCount;
                pCount = 0;
                System.out.println();
            }
        }
    }

    public AVLEntry<K, V> fixAfterDeletion(AVLEntry<K, V> p) {
        if (p == null) {
            return null;
        } else {
            p.height = Math.max(getHeight(p.left), getHeight(p.right)) + 1;
            int d = getHeight(p.left) - getHeight(p.right);
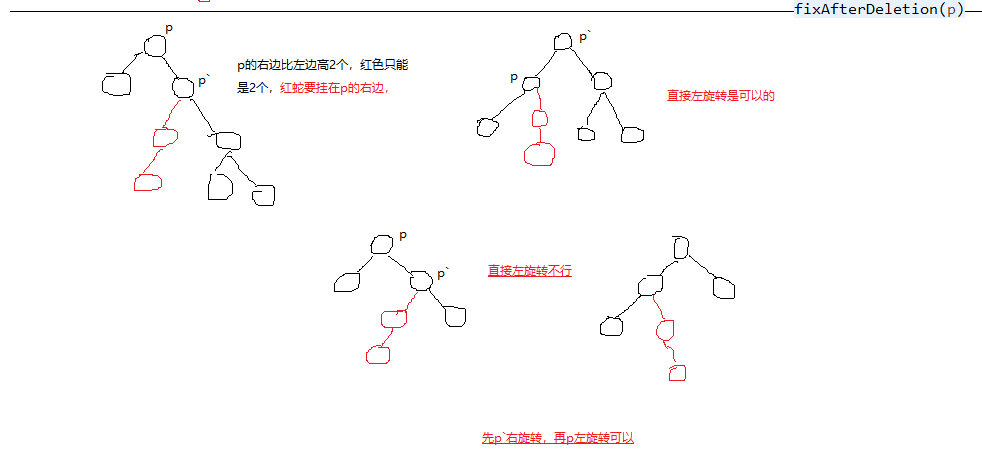
            if (d == 2) {//左节点比右节点高2个，不可能超过2个，一次只加进去一个节点，影响高度是1，是2的时候就已经调整了。
                if (getHeight(p.left.left) - getHeight(p.left.right) >= 0) {
                    p = rotateRight(p);//左边>=右边高可以直接右旋转p。
                } else {
                    p = firstLeftThenRight(p);//右边比左边高，就要先把p.left左旋转，然后在右旋转p。
                }
            } else if (d == -2) {//右节点比左节点高2个
                if (getHeight(p.right.right) - getHeight(p.right.left) >= 0) {
                    p = rotateLeft(p);
                } else {
                    p = firstRightThenLeft(p);
                }
            }
            return p;
        }
    }

    @SuppressWarnings({ "rawtypes", "unchecked", "unused" })
    public static void main(String[] args) {

        AVLMap al = new AVLMap();
        al.put(5d, 55d);
        al.put(4d, 44d);
        al.put(3d, 33d);
        al.put(4.5d, 4.55d);
        al.put(8d, 88d);
        al.put(4.1d, 4.11d);
        al.put(9d, 99d);
        al.put(10d, 100d);
        al.put(6.0d, 6.0d);
        Iterator i = al.iterator();//[{k:4.5,L:{k:4.0,L:{k:3.0},R:{k:4.1}},R:{k:8.0L:{k:5.0},R:{k:9.0,R:{k:10.0}}}},{k:4.0,L:{k:3.0},R:{k:4.1}},{k:3.0}]
        while(i.hasNext()) {
            System.out.println(i.next().toString());
        }
        AVLEntry j = al.getEntry(4.5d);
        al.levelOrder();
        double o =  (Double) al.remove(8d);

        AVLMap<Person, Integer> map = new AVLMap<Person, Integer>(new Comparator<Person>() {
            public int compare(Person o1, Person o2) {
                return o2.id - o1.id;
            }
        });
        for (int i1 = 0; i1 < 16; i1++) {
            map.put(new Person(new Random().nextInt(16),
                    "name" + new Random().nextInt(16)),
                    new Random().nextInt(16));
        }
        Iterator<AVLEntry<Person, Integer>> itr = map.iterator();
        while (itr.hasNext()) {
            System.out.println(itr.next().getKey());
        }

    }
}

public class AVLEntry<K, V> implements Map.Entry<K, V> {
    public K key;
    public V value;
    public AVLEntry<K, V> left;
    public AVLEntry<K, V> right;
    public int height = 1;//单个结点高度就是1
    }
}

public class AVLIterator<K, V> implements Iterator<AVLEntry<K, V>> {//遍歷器

    private Stack<AVLEntry<K, V>> stack;

    public AVLIterator(AVLEntry<K, V> root) {
        super();
        stack = new Stack<AVLEntry<K, V>>();
        addLeftPath(root);//從根開始，最左边都加进去。
    }

    private void addLeftPath(AVLEntry<K, V> p) {
        while (p != null) {
            //p入栈时候，把他的所有子左节点都加里面。右节点不在里面，出来的时候把右节点加进去（这样右节点就在里面了）， 加这个右节点时候同时把所有子左节点加进去。
            //从根开始，所谓的左节点都是入栈时候加进去的，所谓的右节点都是出栈时候加进去的（加这个右节点时候也叫入栈，把所有子左节点加进去）。
            stack.push(p);
            p = p.left;
        }
    }

    @Override
    public boolean hasNext() {
        return stack.isEmpty() ? false : true;
    }

    @Override
    public AVLEntry<K, V> next() {
        AVLEntry<K, V> p = stack.pop();//pop()是要移除元素的。
        addLeftPath(p.right);//pop()出去时候把右节点加进去，加右节点时候把该节点的所有左节点加进去。
        return p;
    }

    @Override
    public void remove() {
        throw new ConcurrentModificationException("Can not remove!");
    }
}