10. Javascript 前后端数据加密

为了加强项目的接口安全程度，需求如下

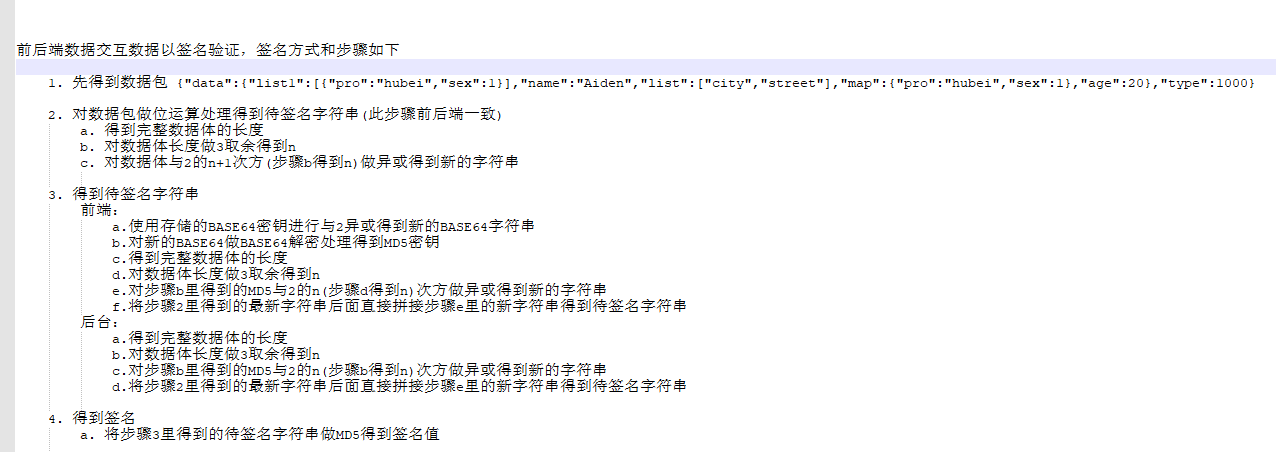
         var options = {
             // 前端需要传送的数据加密
             data: {
                 abc: 123,
                 bcd: 123,
                 cds: '撒旦教付货款12313',
             },
             // 模拟后端返回base64码
             key: 'NWxCZUZ3YWlE'
         }
         var test = function (option) {
             //定义时添加VAR表示是私有属性 内部使用
             var data = option.data; // 前端传送的数据
             var key = option.key; // base64
             //  前端对数据做ascii码排序
             var sort_ASCII = function (obj) {
                 if (obj == null) return '';
                 var arr = new Array();
                 var num = 0;
                 for (var i in obj) {
                     arr[num] = i;
                     num++;
                 }
                 var sortArr = arr.sort();
                 var sortObj = {};
                 for (var i in sortArr) {
                     sortObj[sortArr[i]] = obj[sortArr[i]];
                 }
                 return sortObj;
             }
             // 对象封装 将data转译成字符串
             var changeUrl = function (obj) {
                 if (obj == null) return '';
                 var str = ""
                 var n = 0;
                 Object.keys(sort_ASCII(obj)).forEach(key => {
                     // if (!isNaN(obj[key])) {
                     //     str += (n ? '&' : '') + key + '=' + obj[key];
                     //     n++
                     // }
                     if (!/.*[\u4e00-\u9fa5]+.*$/.test(obj[key])) {
                         str += (n ? '&' : '') + key + '=' + obj[key];
                         n++
                     }
                 })
                 return str
             }
             //  字符串与位异或封装
             var stringToChars = function (_s, _num) {
                 var _r = "";
                 for (var i = 0; i < _s.length; i++) {
                     _r += String.fromCharCode(_s.charCodeAt(i) ^ _num);
                 }
                 return _r.trim().replace(/\s/g, "");
             }
             // 封装内部计算方式
             var remainder = function (str) {
                 var num = Math.pow(2, str.length % 3 + 1);
                 return stringToChars(changeUrl(data), num)
             }
             // 方法前加this表示公共方法 可以在外部访问
             // 获取前后端密钥
             this.getSignature = function () {
                 var code = stringToChars(key, 2)
                 var n = Math.pow(2, code.length % 3);
                 code = stringToChars(md5(code), n)
                 // md5加密前后密钥
                 return md5(remainder(changeUrl(data)) + code)
             }
         }
         var t = new test(options);
         // 生成最后的签名
         console.log(t.getSignature());        

版权声明：本文为小乐9924的原创文章，转载请附上原文出处链接及本声明。