洛谷P5171 Earthquake

题面

题解

我们先把样例画出来：

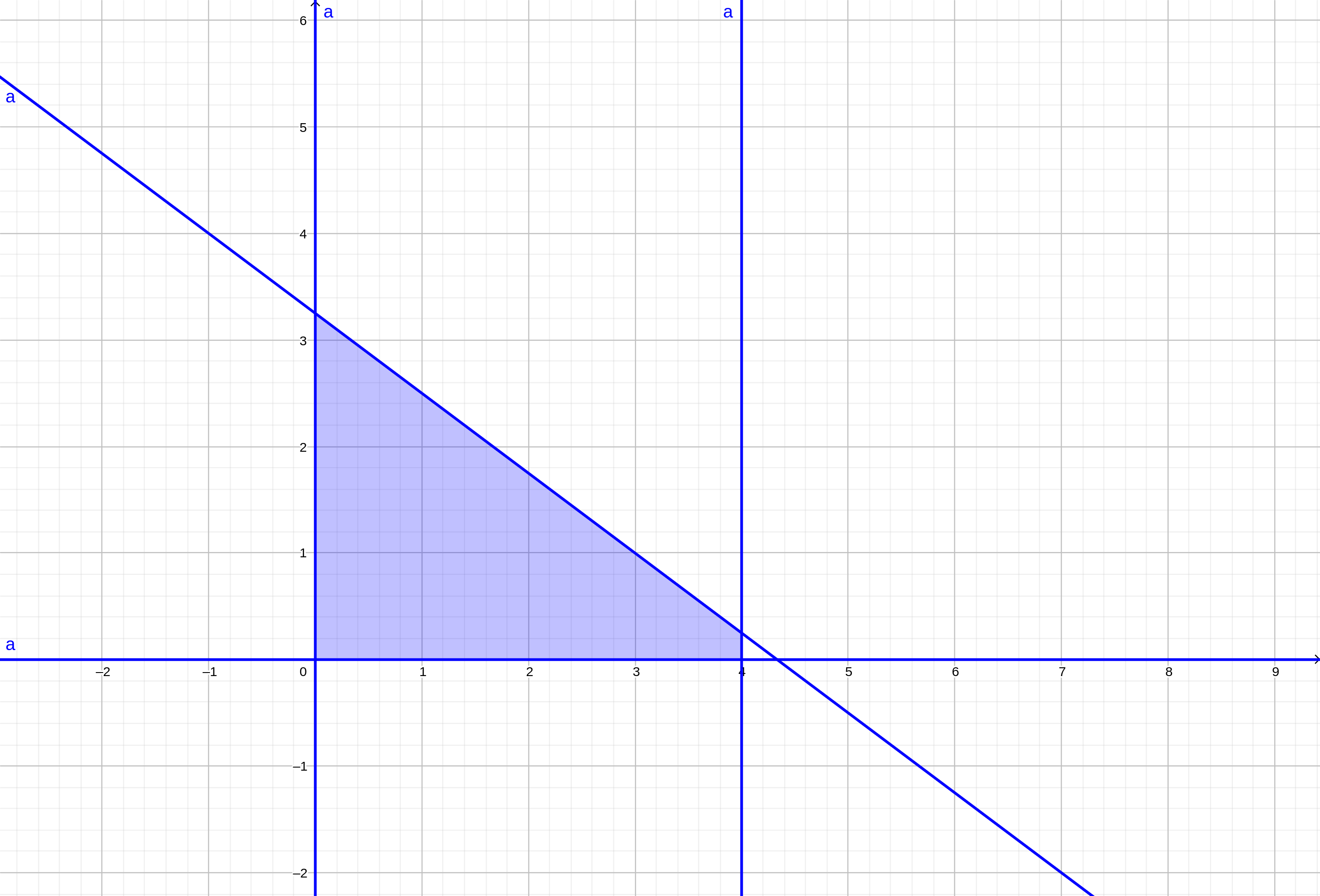
看到它是一个减函数感觉很烦，考虑把函数转过来一下：

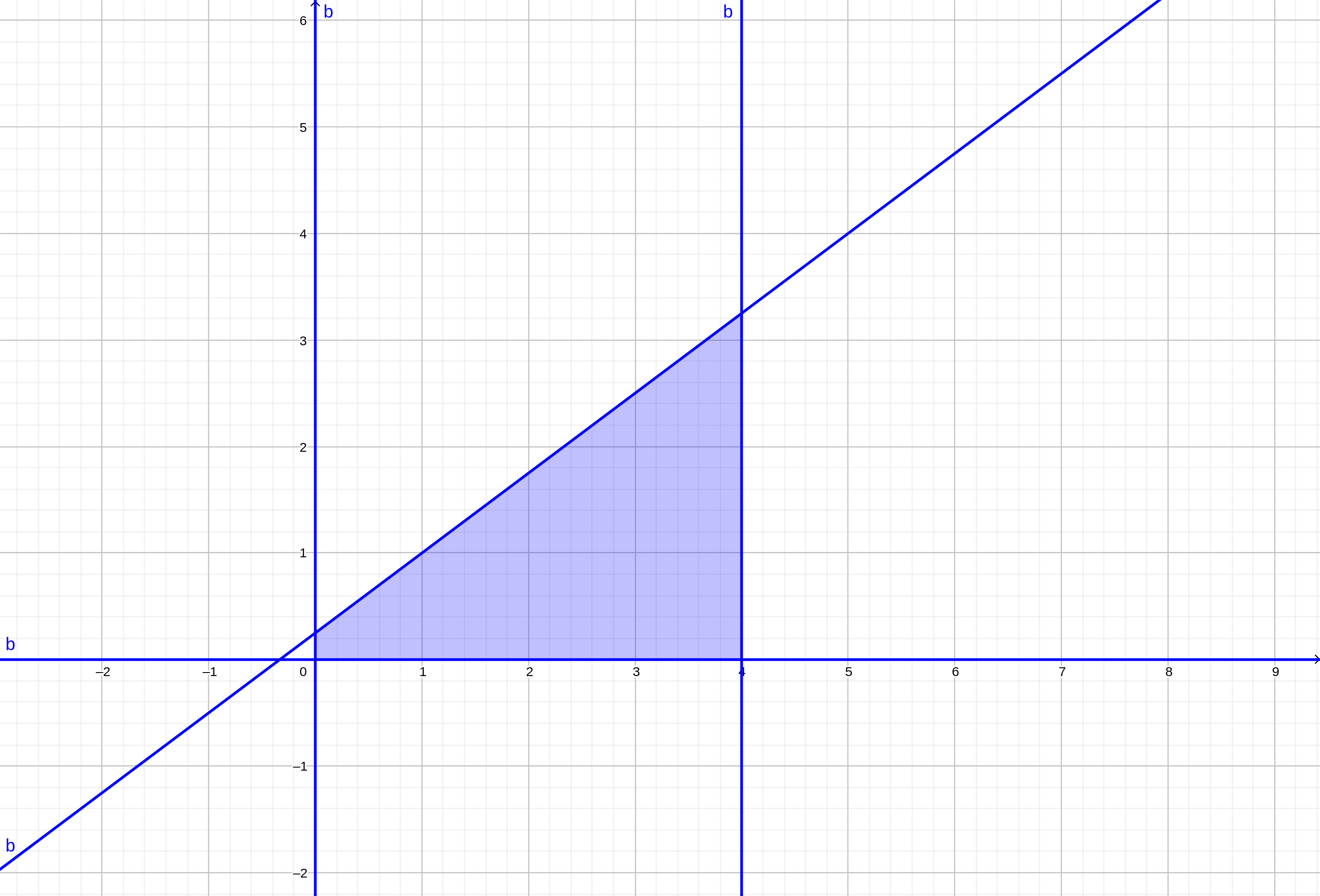
转过来的函数通过推导可得为：

\[y = \frac abx + \frac {c \bmod a}b
\]

于是问题变为了求函数 \(y = \frac {ax + b} c \quad (x \leq n)\)下面的整点数。

讨论两种情况：

\(c \leq a\) 或 \(c \leq b\)

此时斜率或者截距是 \(\geq 1\) 的，考虑将它的斜率或者截距减小。

每次当斜率减小 \(1\) 时，\(x = 1\) 这个位置就会少算 \(1\) 个点，\(x = 2\) 这个位置就会少算 \(2\) 个点,依此类推,可以得出少算的整点数为 \(\sum_{i=0}^n i = \frac {n(n + 1)}2\)。

截距减 \(1\) 同理，可以算出少算的整点数为 \(\sum_{i=0}^n 1 = n + 1\)。

于是我们就可以将斜率和截距减小到 \(< 1\) 的级别了。

可以对着这张图理解一下：

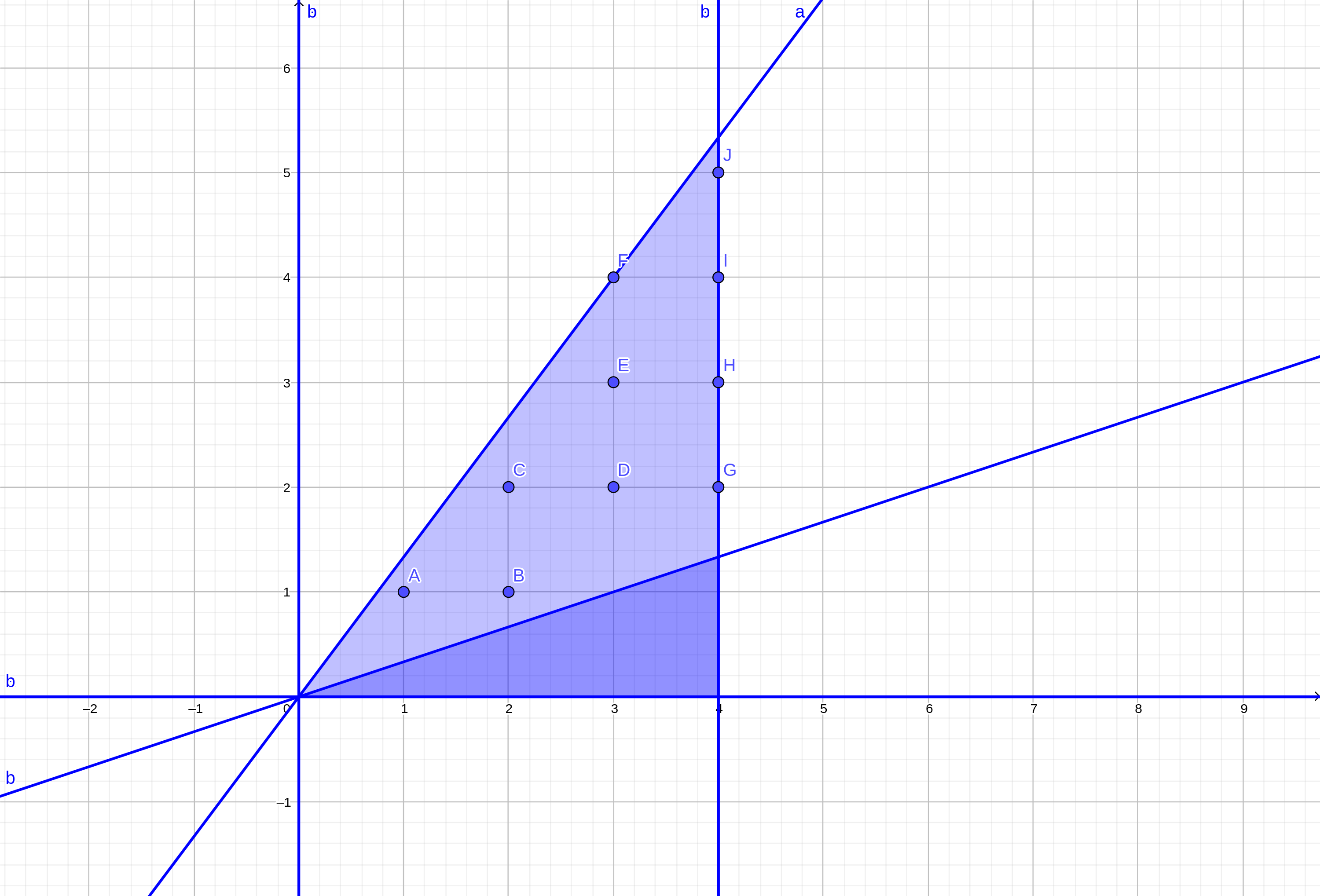
\(c > a\) 且 \(c > b\)

考虑补全成一个矩形，拿总点数减去多出来的三角形个数：

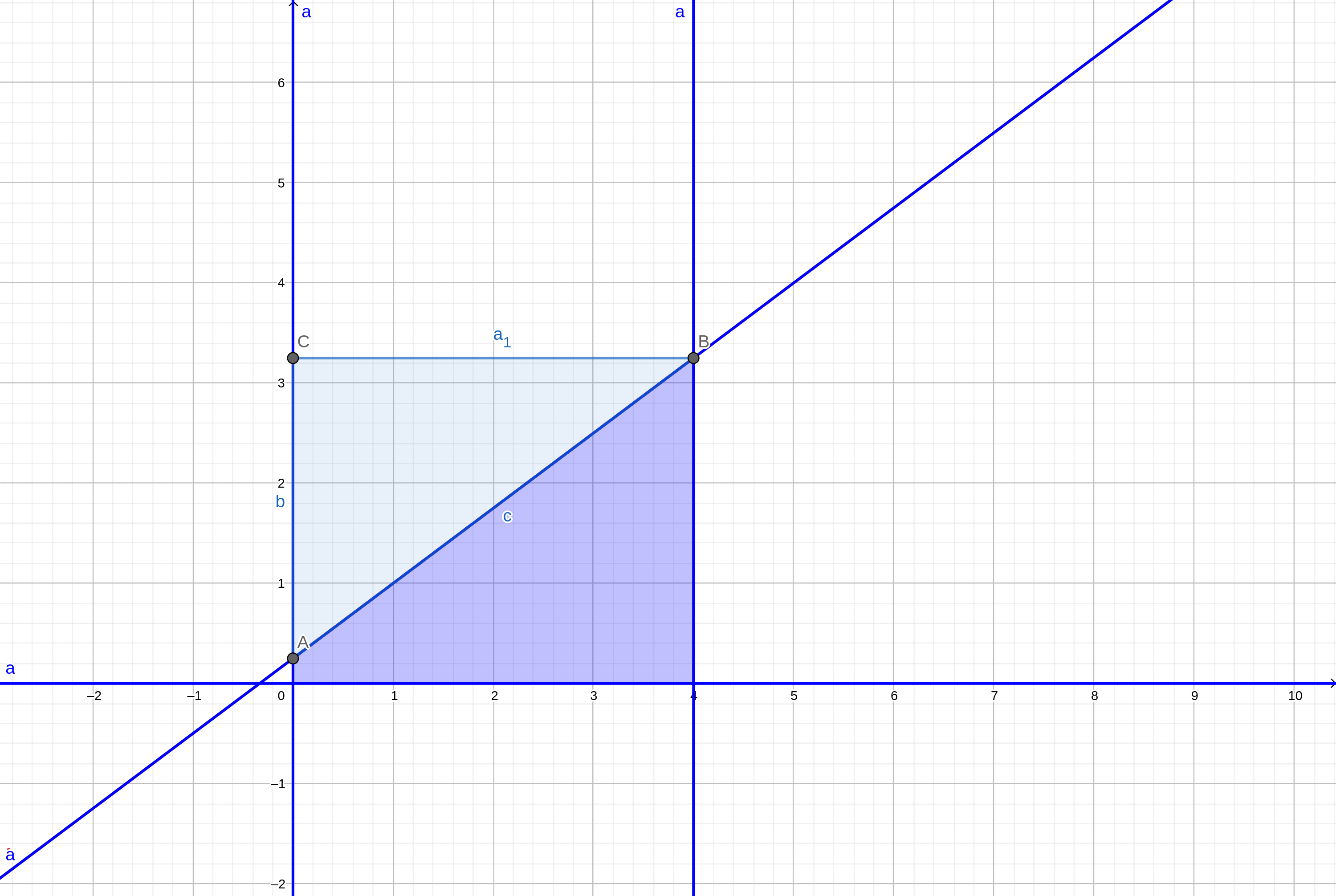
将这个三角形沿着直线 \(y = x\) 翻折一下，可以得出直线 \(y = \frac {ax + b}c\) 沿直线 \(y = x\) 翻折后的直线为 \(y = \frac {cx - b} a\)：

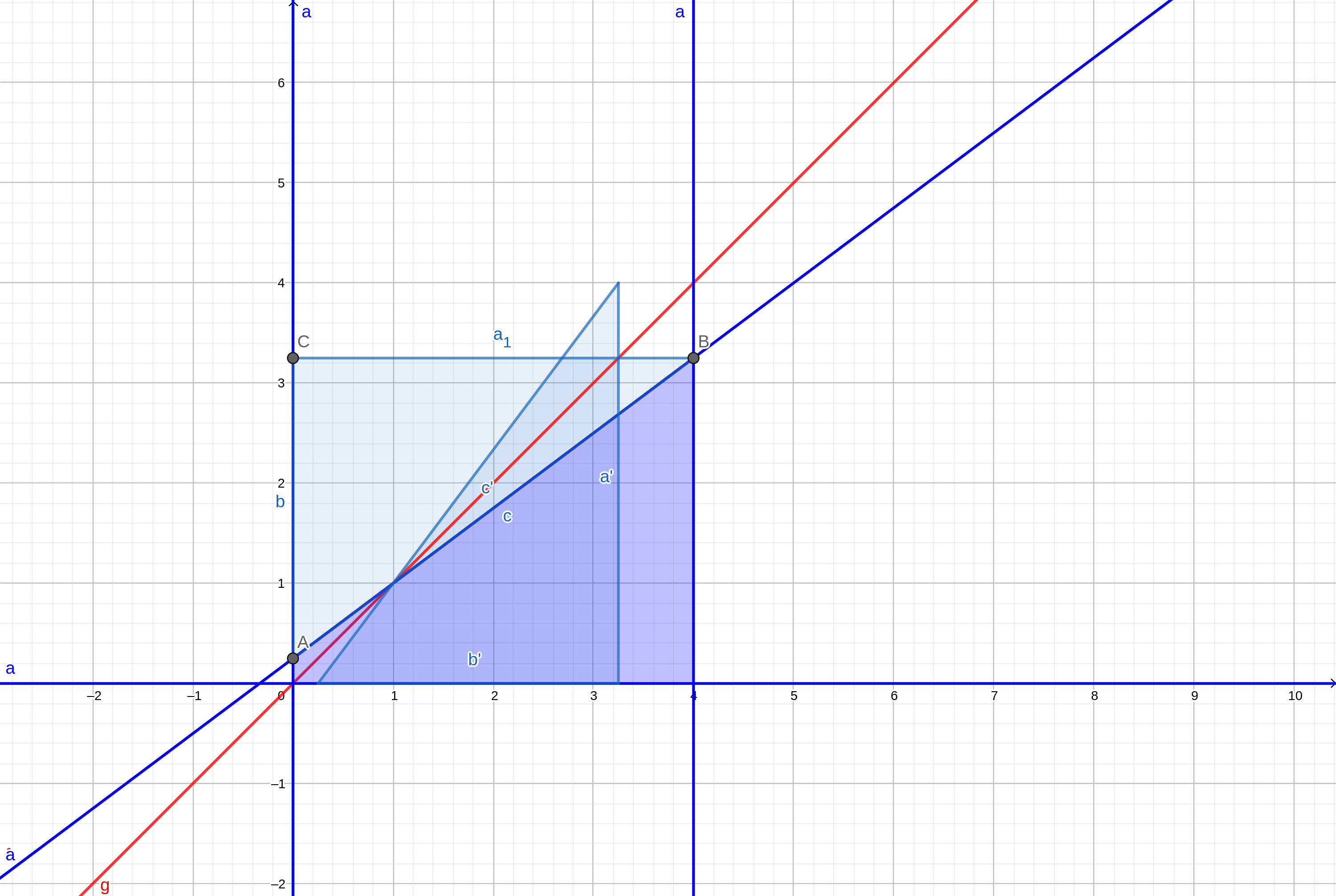
发现这条直线的截距出现了负数，考虑怎么将截距变成正数。

将直线向左平移 \(1\) 个单位即可，可以知道这样做不会对答案有影响。

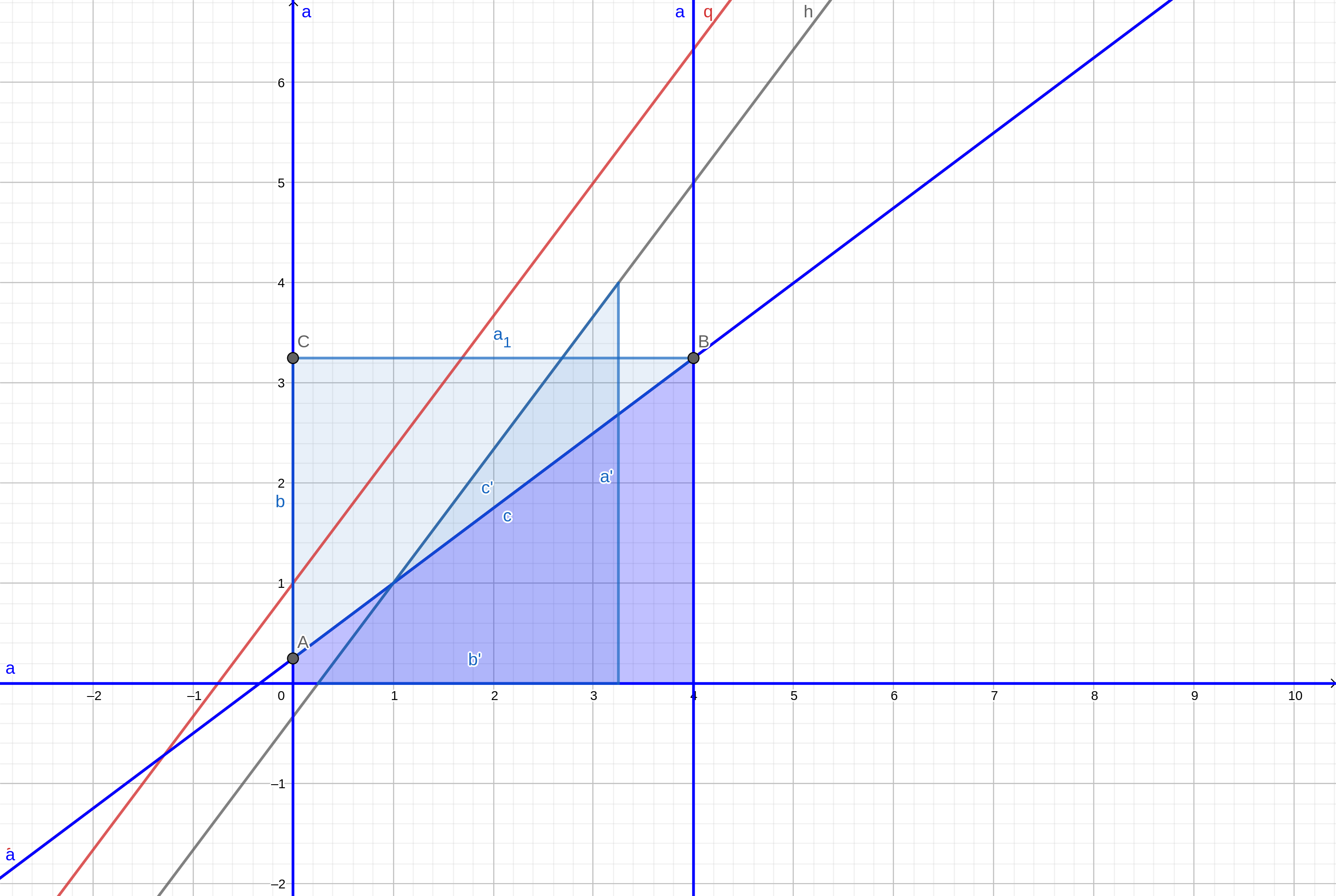
还有一个问题，就是边界线上的点是不能被减掉的，但是我们却把它减掉了。

把截距扰动一下即可，具体来说就是给截距减掉一个较小的数 \(\frac 1a\)，这样就不会算到边界了。

所以这条直线的解析式就变成了 \(y = \frac ca x + \frac {c-b-1}a\)，和代数方法推出来的式子是一样的。如下图所示：

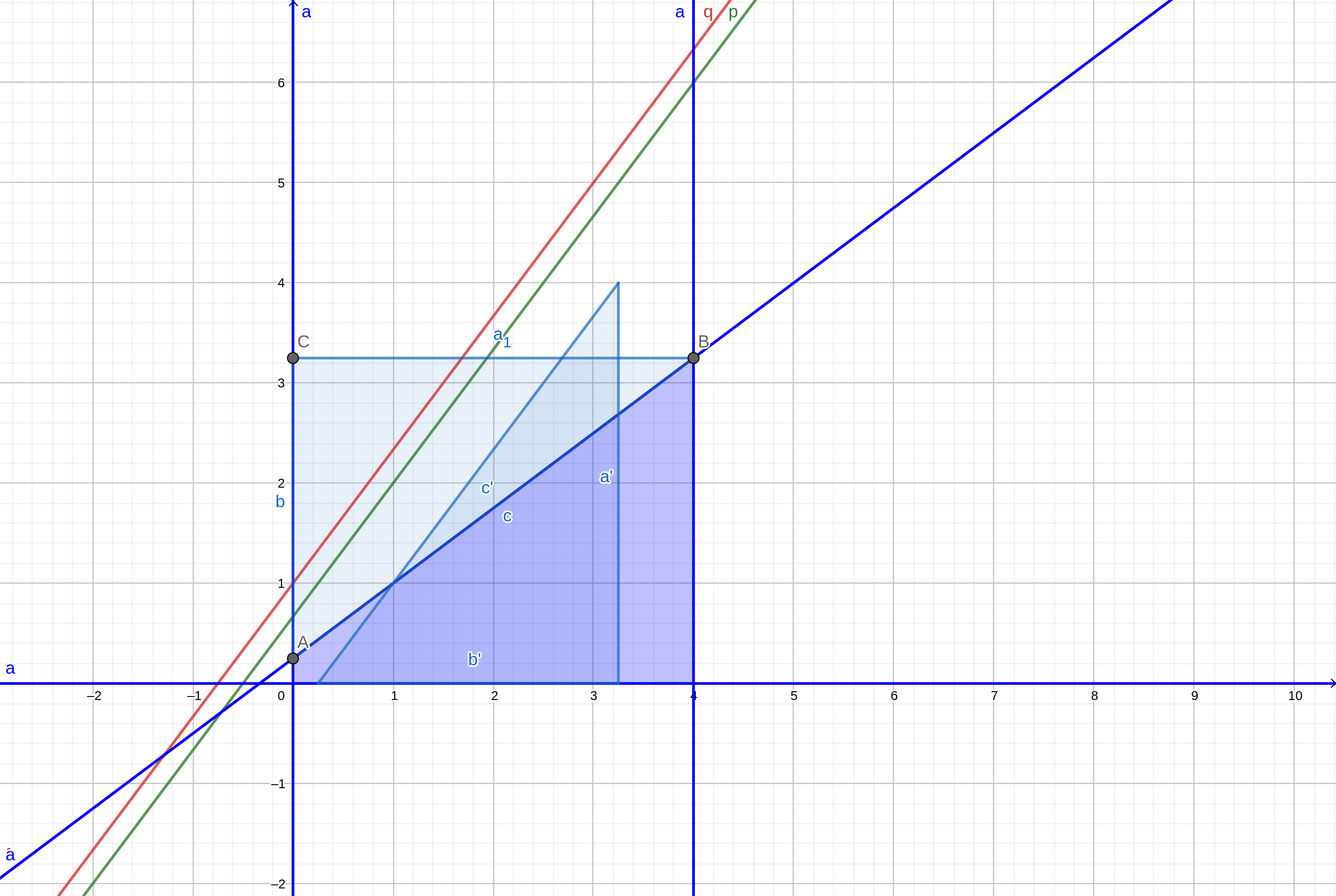
这样我们就可以不用公式而是大量的图片来解决这题了。

代码

#include <cstdio>

long long a, b, c;
long long f(long long a, long long b, long long c, long long n)
{
	if (!a) return b / c * (n + 1);
	if (a >= c || b >= c)
		return n * (n + 1) / 2 * (a / c) + (n + 1) * (b / c) + f(a % c, b % c, c, n);
	long long m = (a * n + b) / c;
	return n * m - f(c, c - b - 1, a, m - 1);
}

int main()
{
	scanf("%lld%lld%lld", &a, &b, &c);
	printf("%lld\n", f(a, c % a, b, c / a) + c / a + 1);
	return 0;
}