C#利用控件mscomm32.ocx读取串口datalogic扫描枪数据

1）.开发环境VS12,语言C#

2）.扫描枪品牌:datalogic 4470

3）.通讯协议：串口

1.首先，第一步创建一个新工程，windows窗体应用程序，命名为TestScanner，如下：

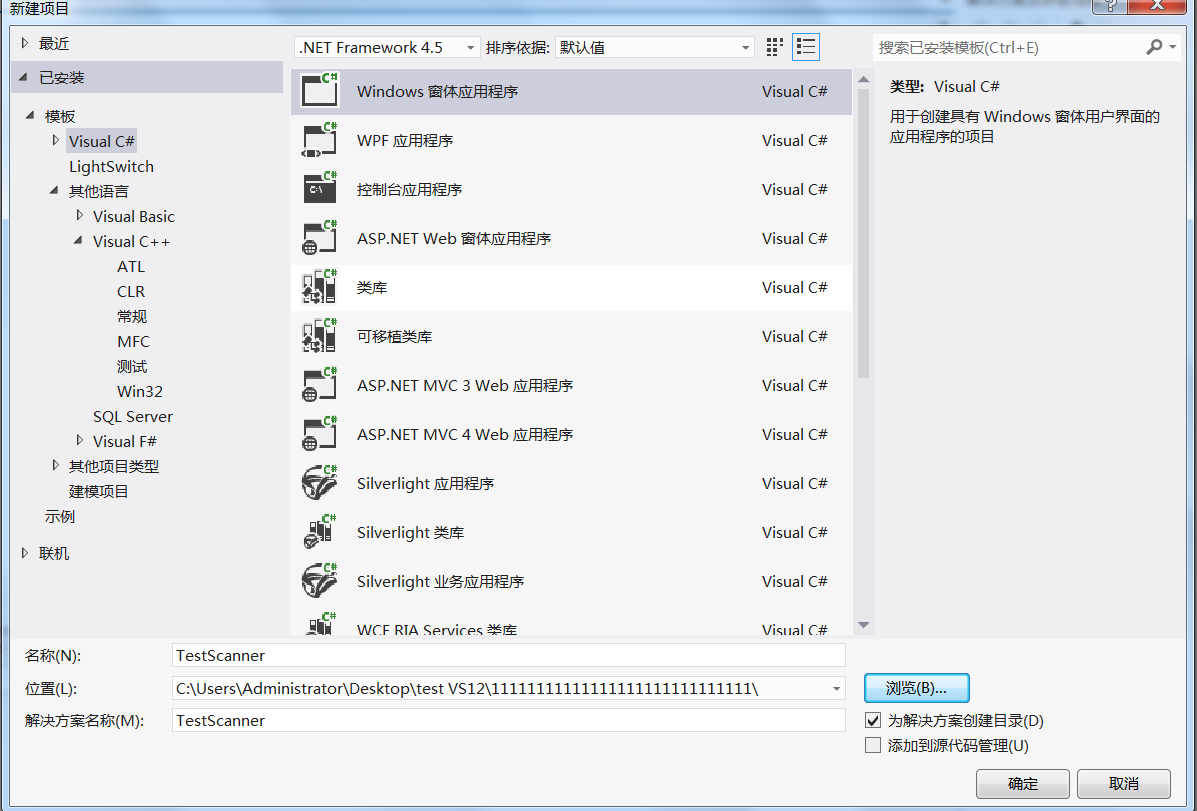
2.选择 “工具”-“选择工具箱”，如下：

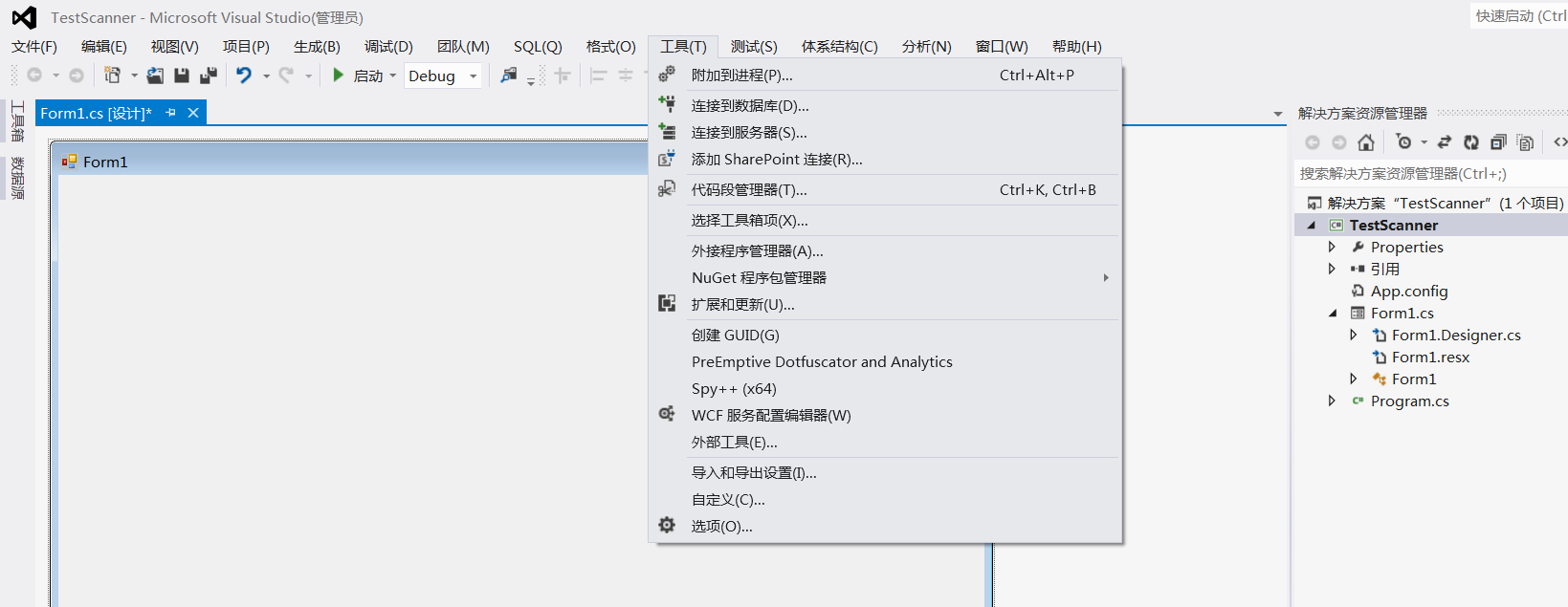
3.选择"microsoft communication control version 6.0"，通过此路径可知其位于64位SysWow64下的ocx控件mscomm32.ocx;

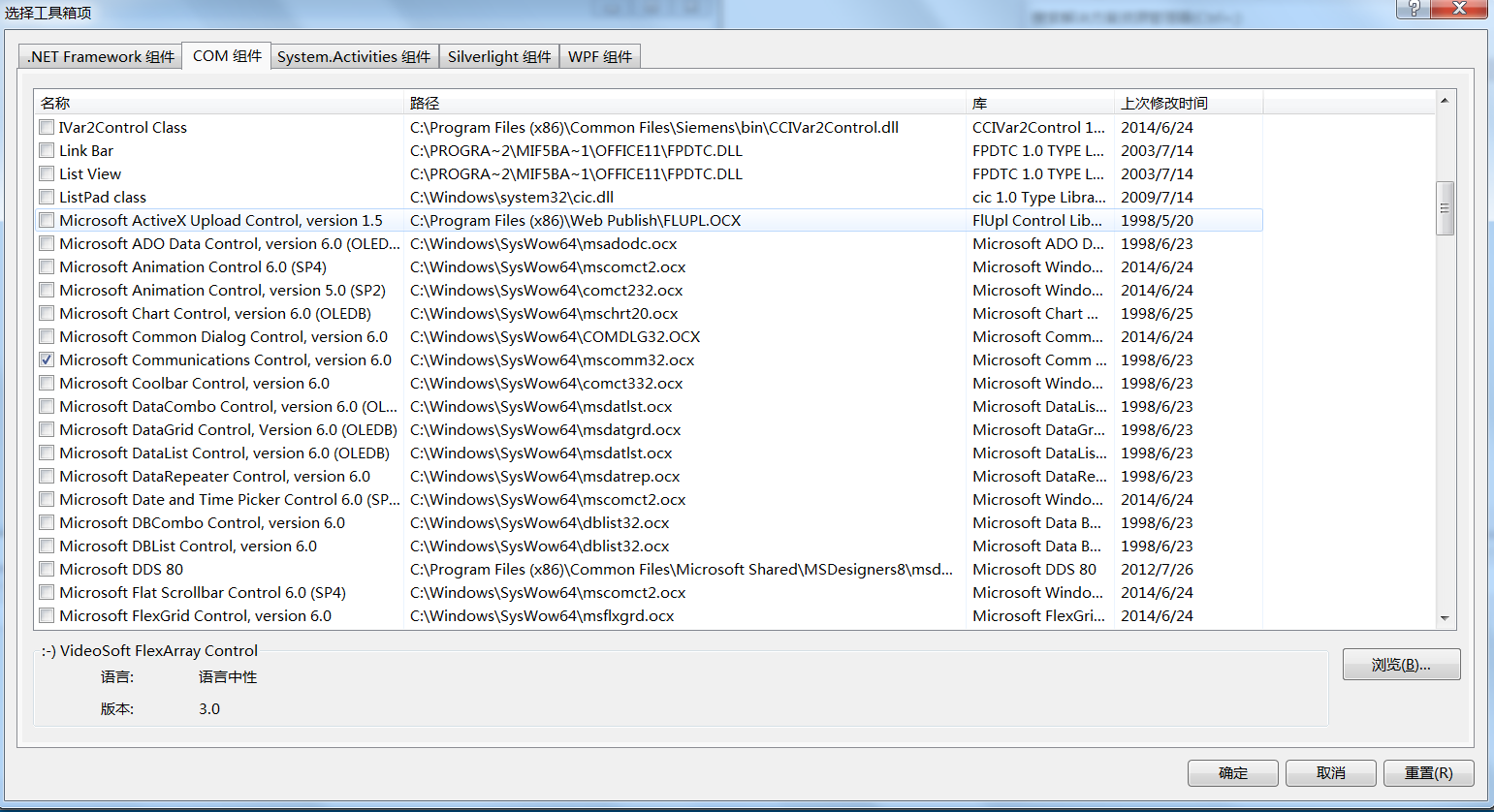
4.从右侧工具箱“组件”中找到串口控件，拖入窗体Form1中，命名为MD_MSComm,并在界面初始化中填入相关参数：

MD_MSComm.CommPort = 11;

MD_MSComm.InputMode = MSCommLib.InputModeConstants.comInputModeText;
MD_MSComm.InBufferSize = 1024;
MD_MSComm.OutBufferSize = 512;
MD_MSComm.Settings = "9600,n,8,1";

MD_MSComm.SThreshold = 0;
MD_MSComm.RThreshold = 1;//first byte trigger oncomm event
MD_MSComm.InBufferCount = 0;
MD_MSComm.OutBufferCount = 0;
MD_MSComm.PortOpen = true;

5.在控件MD_MSComm的事件中添加“OnComm”事件，并读取扫码枪数据代码如下：

string str="";
if (MD_MSComm.CommEvent > 1000) //CommEvent属性值，不同值代表不同的串口状态，若为2，代表有数据，可供读取；
{
Log4netHelper.Error(this.GetType(), "communication error, the value is:" + MD_MSComm.CommEvent.ToString());
return;
}
if (MD_MSComm.CommEvent == 2)
{
if (MD_MSComm.InBufferCount > 0)//串口缓存区的数据长度
{
str = ((string)MD_MSComm.Input).Trim();//input方法 来读取串口枪缓冲区的数据

if (str.Length == 14)
{
AvailablePublicHelper.CurScanner = str;
Log4netHelper.Info(this.GetType(), "get the content of the scanner is:" + str);
}
else
{

Log4netHelper.Warn(this.GetType(), "get the content of the scanner is not normal:" + str);
}
}
}

6.配置硬件扫码枪的读取方式，为了调试方便，本文选择的持续读取模式，若希望选择命令触发读取形式，需每次发送读取命令“02”至串口，读取命令，可在串口配置中进行设置，具体品牌可根据扫码枪供应商来协商；

命令写入数据到扫码枪的方式为MD_MSComm.output;

7.将扫码枪串口插入到工控机硬件接口，并和程序中的comport值匹配，本文选择的comm口为11；

8.结束。