LOJ 3119: 洛谷 P5400: 「CTS2019 | CTSC2019」随机立方体

题目传送门：LOJ #3119。

题意简述：

题目说的很清楚了。

题解：

记恰好有 \(i\) 个极大的数的方案数为 \(\mathrm{cnt}[i]\)，则答案为 \(\displaystyle\frac{\mathrm{cnt}[k]}{(nml)!}\)。

“恰好”这个词非常的难受，我们考虑容斥：

记 \(\mathrm{f}[i]\) 为存在 \(i\) 个极大的数，且若恰好有 \(j\) 个极大的数，会被相应地统计 \(\displaystyle\binom{j}{i}\) 次的方案数。

则有：\(\displaystyle\mathrm{f}[i]=\sum_{j}\binom{j}{i}\mathrm{cnt}[j]\)。

根据二项式反演，有：\(\displaystyle\mathrm{cnt}[i]=\sum_{j}(-1)^{j-i}\binom{j}{i}\mathrm{f}[j]\)。

问题转化为求出每一个 \(\mathrm{f}[i]\)。

---

首先考虑以下事实：

• 不会有超过 \(\min(n,m,l)\) 个极大的数。

• 每两个极大的数必然不可能有任意一维的坐标相同，这是因为每个极大的数需要大于所有与它有任意一维坐标相同的点上的数。

• 若至少存在 \(i\) 个极大的数，则有 \(i\) 行，\(i\) 列和 \(i\) 个纵截面被至少一个极大的数“控制”。

所以，剩余的 \((n-i)(m-i)(l-i)\) 个数是没有任何限制的，这是因为我们仅需保证至少存在 \(i\) 个极大的数。若剩下的数中又出现了极大的数也没关系，这实际上并不在考虑范围内。

又有，极大的数的条件仅和大小关系有关，而与数的绝对大小无关，所以可以看作乘上了一个“\(nml\) 取出 \((n-i)(m-i)(l-i)\) 个数进行排列的方案数”，即一个排列数的系数，而剩下的需要单独考虑。

但是先别着急，我们先写出目前得到的式子（下列式子中均将排列数写作下降幂的形式）：

\[\mathrm{f}[i]=\left(n^{\underline{i}}m^{\underline{i}}l^{\underline{i}}\right)\times\left((nml)^{\underline{(n-i)(m-i)(l-i)}}\right)\times\mathrm{g}[i]
\]

第一个括号代表有顺序地选出（即一个排列）\(i\) 个三维坐标均互不相同的点，这个顺序即为之后的大小顺序。

第二个括号代表对无关点进行标号，也是一个排列数。

而 \(\mathrm{g}[i]\) 代表在剩下的 \(nml-(n-i)(m-i)(l-i)\) 个点中按照规定的大小顺序进行标号的方案数。

---

接下来我们考虑求出 \(\mathrm{g}[i]\)：

让我们先考虑 \(i\) 个极大值中最大的那个，它的位置已经被确定了，它的值也被确定为可选的值中的最大的那一个，而所有与它有关联（有一维坐标相同）的位置都强制小于它。

但是，先等等！这些位置上的数，不一定只有最大值给予的一个限制，如果这个位置同时和其它极大值有关联，那么不能单纯用只最大值对其进行限制。

不过呢，其实这是没有影响的，我们只需要管那些“只和最大值有关联”的位置，若和其它极大值有关联，我们放到之后再去处理即可。

从这里就可以看出先考虑最大值的高明之处，因为越小的极大值的限制越严格，我们采取从大到小考虑的方式，就可以只考虑最后的限制。

而考虑完最大值以及“只和最大值有关联”的位置后，次大值的数值就应该为剩下的值中最大的那一个。

按照上述方式类推：对于最大的极大值，只要考虑那些和最大值有关联的部分，但是必须去除和“比最大值小的极大值”有关联的位置。

对于次大的，只要考虑和次大值有关联的部分，但是要去掉和“比次大值小的极大值”有关联的位置。

以此类推……

为了便于理解，我们展示 \(n=8,m=11,i=5\) 时的二维示例图（你也可以理解为 \(l=1\) 的三维情况）：

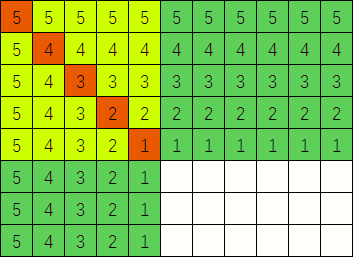
因为极大值的位置与答案无关，为了方便，按照从小到大的顺序从左上角依次排下。

白色是无关位置，橙色是极大值所在位置，深绿色是仅和一个极大值有关联的位置，黄绿色是同时和两个极大值有关联的位置。

对于不是无关位置的格子，写上的数就表示它是在第几轮被考虑的。

可以看出，深绿色部分在考虑对应的极大值时的同一轮时就被统计，而黄绿色部分须等到对应的较小的极大值的同一轮才会被统计。

这张图的填数模式是浅显易懂的，很简单就能看出其中规律。

尝试写出其对应的 \(\mathrm{g}[i]\) 的值吧：\(\mathrm{g}[i]=69^{\underline{9}}\cdot 59^{\underline{11}}\cdot 47^{\underline{13}}\cdot 33^{\underline{15}}\cdot 17^{\underline{17}}\)。

每个下降幂（排列数）就对应着相应的轮数，例如第一轮中是 \(69\) 个数选出 \(9\) 个来排列。

进一步地，我们尝试写出形式化的公式（为了方便表述，定义记号 \(\varrho(x)=(n-x)(m-x)(l-x)\)）：

对于某个 \(i\) 值的第 \(i-j+1\) 轮，换句话说，也就是图中从外往里数的第 \(j\) 层，

之前填完剩余的数的数量为 \(nml-(n-j)(m-j)(l-j)-1\) 个，即 \(\varrho(0)-\varrho(j)-1\)，

而需要填的位置的数量为 \((n-j+1)(m-j+1)(l-j+1)-(n-j)(m-j)(l-j)-1\) 个，即 \(\varrho(j-1)-\varrho(j)-1\)。

所以就需要乘上：从“剩余的数”中取出“需要填的位置”那么多数进行排列以填入位置中的方案数，也就是一个排列数。

则 \(\displaystyle\mathrm{g}[i]=\prod_{j=1}^{i}(\varrho(0)-\varrho(j)-1)^{\underline{\varrho(j-1)-\varrho(j)-1}}\)。

写成阶乘的形式就是 \(\displaystyle\mathrm{g}[i]=\prod_{j=1}^{i}\frac{(\varrho(0)-\varrho(j)-1)!}{(\varrho(0)-\varrho(j-1))!}\)。

这时就一目了然了，不难化成如下形式：

\[\mathrm{g}[i]=(\varrho(0)-\varrho(i)-1)!\prod_{j=1}^{i-1}\frac{1}{\varrho(0)-\varrho(j)}
\]

---

那么，将 \(\mathrm{g}[i]\) 代回 \(\mathrm{f}[i]\) 中吧！

\[\begin{aligned}\mathrm{f}[i]&=\left(n^{\underline{i}}m^{\underline{i}}l^{\underline{i}}\right)\times\left((nml)^{\underline{(n-i)(m-i)(l-i)}}\right)\times(\varrho(0)-\varrho(i)-1)!\prod_{j=1}^{i-1}\frac{1}{\varrho(0)-\varrho(j)}\\&=\left(n^{\underline{i}}m^{\underline{i}}l^{\underline{i}}\right)\frac{(nml)!}{(nml-\varrho(i))!}(nml-\varrho(i)-1)!\prod_{j=1}^{i-1}\frac{1}{nml-\varrho(j)}\\&=\left(n^{\underline{i}}m^{\underline{i}}l^{\underline{i}}\right)(nml)!\prod_{j=1}^{i}\frac{1}{nml-\varrho(j)}\end{aligned}
\]

则答案为：\(\displaystyle\frac{\mathrm{cnt}[k]}{(nml)!}=\frac{1}{(nml)!}\sum_{i}(-1)^{i-k}\binom{i}{k}\mathrm{f}[i]\)

注意到和 \(\mathrm{f}[i]\) 里面的 \((nml)!\) 抵消掉了，干脆两边都不写了吧：

\[\tilde{\mathrm{f}}[i]=\left(n^{\underline{i}}m^{\underline{i}}l^{\underline{i}}\right)\prod_{j=1}^{i}\frac{1}{nml-\varrho(j)}
\]

\[\mathbf{Ans}=\sum_{i}(-1)^{i-k}\binom{i}{k}\tilde{\mathrm{f}}[i]
\]

---

接下来就是最后的问题，我们需要在均摊 \(\mathcal{O}(1)\) 的时间内求出每个 \(\mathrm{f}[i]\)（\(0\le k\le\min(n,m,l)\)）。

可以发现瓶颈在于求逆元上，只要用到这题的方法就可以了。

下面是代码：

#include <cstdio>

typedef long long LL;
const int Mod = 998244353;
const int MN = 5000005;

void exgcd(int a, int b, int &x, int &y) {
	if (!b) x = 1, y = 0;
	else exgcd(b, a % b, y, x), y -= a / b * x;
}
inline int Inv(int a) {
	int x, y;
	exgcd(a < 0 ? a + Mod : a, Mod, x, y);
	return x;
}

int Invs[MN];
inline void Init(int N) {
	Invs[1] = 1;
	for (int i = 2; i <= N; ++i)
		Invs[i] = -(LL)(Mod / i) * Invs[Mod % i] % Mod;
}

int N, M, L, Q, K, Ans;
int Vals[MN], iVals[MN];

inline int R(int x) { return (LL)(N - x) * (M - x) % Mod * (L - x) % Mod; }

int main() {
	Init(5000000);
	int T; scanf("%d", &T);
	while (T--) {
		scanf("%d%d%d%d", &N, &M, &L, &K), Ans = 0;
		Q = N < M ? N < L ? N : L : M < L ? M : L;
		iVals[0] = 1;
		for (int i = 1; i <= Q; ++i)
			Vals[i] = R(0) - R(i),
			iVals[i] = (LL)iVals[i - 1] * Vals[i] % Mod;
		int iV = Inv(iVals[Q]);
		for (int i = Q; i >= 1; --i)
			iVals[i] = (LL)iV * iVals[i - 1] % Mod,
			iV = (LL)iV * Vals[i] % Mod;
		int C = 0, S = 1;
		for (int i = 1; i <= Q; ++i) {
			S = (LL)S * R(i - 1) % Mod * iVals[i] % Mod;
			if (i == K) C = 1;
			if (i > K) C = -(LL)C * i % Mod * Invs[i - K] % Mod;
			Ans = (Ans + (LL)C * S) % Mod;
		}
		printf("%d\n", Ans < 0 ? Ans + Mod : Ans);
	}
	return 0;
}

感谢 @Winniechen 与我交流做法。