【2018.12.10】NOI模拟赛3

题目

WZJ题解

大概就是全场就我写不过 $FFT$ 系列吧……自闭

T1

奶一口，下次再写不出这种 $NTT$ 裸题题目我就艹了自己 -_-|||

而且这跟我口胡的自创模拟题 $set1$ 的 $T3$ 差不多啊……我之前口胡那题甚至还改简单了点（因为忘了 $FFT$ 可以套分治优化）。

注意，分治 + $FFT$ ≠ 分治$FFT$ ！！！

分治 + $FFT$ 是用分治来卷一堆背包，并且这些背包的总大小是祖传级别的！！！

分治$FFT$ 跟 $FFT$ 求的式子都不一样。

基础知识：n点无根树，问包含恰好k个点的连通子图的最大权，点上有权，k∈[1,n]。

$f(x,k)$ 以 $x$ 为根子树包含 $k$ 个点的最大权。

这就是以前说过的那个假 $O(n^3)$ 复杂度的 $dp$，不说了。

这题其实就是给了一堆环，然后问随机放 $k$ 个人，使每个环上至少有 $1$ 个人的概率。

像这种概率问题，我们先把它转化成方案数，因为 概率 $=$ 满足要求的方案数 $/$ 总方案数。

一提到方案数，我们就想到这个可以用传统的背包做……

就是对于每个环，预处理出在这个环上分别放 $1$ 到 $size$ 个人的方案数。

可以证明这样全局有 $n$ 个方案数。

然后就要用一种类似于合并背包的方法，把这堆总大小为 $n$ 的背包合并成一个。

啥叫合并背包？

考虑这么一个问题：有两个背包各自维护一个集合，背包的第 $i$ 位表示 自己的集合中有多少个值为 $i$ 的数。

然后让你求 两集合的所有数两两配对相加后，得到的数的集合。

假设一个集合中有 $x$ 个值为 $i$ 的数，另一个集合中有 $y$ 个值为 $j$ 的数，根据题意（两两配对相加）和乘法原理，可知新集合会有 $x\times y$ 个值为 $i+j$ 的数。

由于需要用两重循环枚举两个背包中配对的数，所以时间复杂度是 $O(n^2)$。

这就是合并背包。

但这样合并的时间显然升天了！怎么优化？

其实合并背包有个定性优化，我们只需要观察合并背包的式子就发现了——

$$C_{i+j}=\sum_{i=1}^{size(A)} \sum_{j=1}^{size(B)} A_i\times B_j$$

这就是裸的 $FFT$ 式子啊！此时合并两个背包的时间复杂度只有 $O(n\times log(n))$ 了（有一堆常数）。

但是这题有一堆背包，那时间复杂度还要再乘个玄学值，可能会超时。

所以考虑快速合并大量背包的做法。这里有两种，一种是 分治+$FFT$，一种是 按秩合并（即每次合并两个大小最小的背包）。

分治+$FFT$ 就是分治合并一堆背包，时间复杂度是 $O(n\times log^2(n))$ 带巨大常数（因为分治的每层中，合并一些总长为 $n$ 的背包的总时间复杂度略高于 $O(n\times log(n))$）；

按秩合并（启发式合并）类似于哈夫曼编码的原理，这种做法的时间复杂度其实比较玄学，但实测跟 分治+$FFT$ 的效率差不多。

由于这题需要取模，所以把 $FFT$ 全改成 $NTT$。

T2

防 $AK$ 题

$30pts$ 轮廓线 $dp$ 裸题。

$50pts$ 改进一下，一行一行转，那么枚举相邻两行的所有状态，预处理一个 $(2^m)^2$ 大小的转移矩阵。然后矩阵快速幂转移。时间复杂度 $O((2^m)^3\times log(n))$。

$65pts$ 发现 $log$ 直接爆出去了，所以二进制快速幂改成十进制快速幂。

$0$ 到 $9$ 分成 $2$ 的若干次方

原理……像循环展开吧。

$80pts$ 把那些没用的转移去掉。

具体怎么去掉呢？我们发现每次转移既然都是对应一个固定的转移矩阵，也就是说每相邻两层的转移 都是上一层的所有 $m$ 种状态点 向下一层的所有 $m$ 种状态点连有向边，这样最多有 $2^{2m}$ 条边。这是个有环图，也就是说转移若干层（最多 $256$ 层）后，就会回到原来的一种状态。这样我们就发现有些情况的入度是 $0$，即没有任何状态能转移到它，那这些状态就是没用的，在预处理转移矩阵的时候就不放它们，对剩下的有用状态照常处理。实测 $m=8$ 时只有 $71$ 个有用状态。

T3

tag：树状数组+链上二分。

暴力的做法就是取出查询的链，然后扫两遍，求带权中位点（就是找一个位置，使两边的权值差的绝对值最小）。时间复杂度 $O(q\times n)$。

这种题显然需要数据结构维护（虽然我不是很会在树上套数据结构）。

我们可以拆出 $3$ 个部分：

1. 单点修改

2. 找出一条链上的带权中位点

3. 求链上所有点到其带权中位点的带权距离和（附加的那一堆深度……明显是等差数列，等差数列）

$2$ 操作是决策操作，所以首先考虑定死的 $1,3$ 操作能否同时完成。

有一种可以维护树上链权和的数据结构，叫树状数组。

首先单点修改可以看成减一个数再加一个数，也就是单点加。开个数组记一下每个位置上的数即可。

为了记链权和，我们在单点加时 给以修改点为根的子树的所有点都加上同样的加数。由于子树是一段连续的 $dfs$ 序区间，所以子树加的操作 用以 $dfs$ 序为下标的树状数组 随便维护就行了。

然后假设一条链的两端点为 $x,y$，$lca$ 为 $x$（$y$ 同理），如图

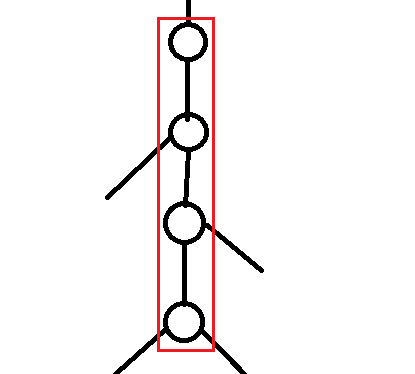
我们定义一个点的权值为从根节点到这个点的路径上所有点的 数值 $\times$ 深度 的和，则这段链的权值和为 $T(y)-T(fa(x))$。

其中 $fa(i)$ 为点 $i$ 的父亲，$T(i)$ 为以点 $i$ 的权值，深度是指在整棵树中的深度。

其实就是普通前缀和的思想。一个点到根的路径的权值和 只会受到它所有祖先的影响，而你在更改祖先时就已经把包括这个点在内的所有子孙都更新了，所以查询的时候直接前缀相减就行了。

同时，我们还解决了区间统计时，深度的递增所带来的影响。

那么对于 求链上所有点到其带权中位点的带权距离和 这个问题，我们就可以把一条两端为点 $x,y$，$lca$ 为 $L$ 的链拆成 $3$ 条像上面一样的不拐弯的链：

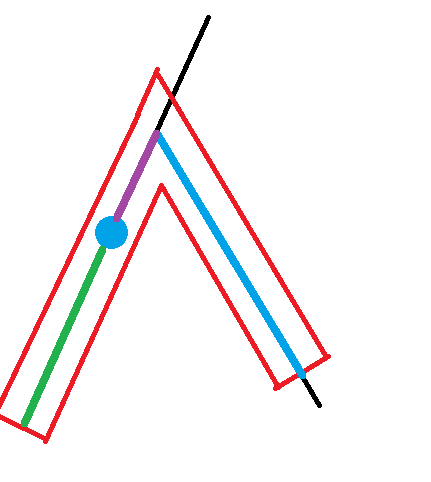
假设蓝点是中位点，其编号为 $k$，则绿色链很好处理，其贡献为 $[T(x)-T(fa(k))]-sum(k,x)\times depth(k)$，其中 $sum(k,x)$ 为 从点 $k$ 到点 $x$ 的所有点上的数的和；

蓝色链也很好处理，其贡献为 $[T(y)-T(fa(L))]-sum(L,y)\times [depth(k)-depth(L)]$；

紫色链就麻烦点，因为这部分的深度是倒过来计算的，所以贡献为 $sum(L,k)\times depth(k) - [T(k)-T(fa(L))]$。

那最后的问题就是……查询链上所有点上的数的和？

再维护一个树状数组，像维护链上的权值和一样做就行了。

然后考虑能否在此基础上再支持 $2$ 操作。

首先我们得知道找带权中位点的本质：找一个点，使得两侧的点权和的差最小（这里的差肯定要取绝对值）。

有个很暴力的做法，就是我们发现 在移动假想中位点的时候 两侧的点权和的差值变化 是个二次函数图像。

所以我们可以直接链上三分，找出差值的最小值所在处。这样的话就得快速移动假想中位点，需要用倍增或树剖。总时间复杂度是 $O(n\times log^3(n))$ 的，带上大常数，卡不过……

先不管树剖，如果我们用的是倍增，我们会发现三分和倍增移动其实是同一类东西，两者可以合并。

也就是说，可以从底部倍增往上跳，然后找到第一个两侧差值变号的位置，暴力判断它和相邻的点谁绝对差值更小就行了。

考虑到链会在 $lca$ 处打折，把链以 $lca$ 为界拆成两半，分别找这个位置，然后再取最优者就行了（其实很显然，至少有一边找到的位置是 $lca$）。

这个做法叫链上二分，但实际上只用了倍增。总时间复杂度 $O(n\times log^2(n))$。