浅谈算法——Manacher

字符串算法在各大高级比赛中均有用到，所以，学习好字符串算法对我们而言十分重要。那么，今天我们就给大家介绍一个快速求回文串的算法，Manacher算法，我们也习惯性叫它马拉车算法。

一.引入

首先我们要知道什么是回文串——当一个字符串它从右到左和从左到右读是一样的，我们就称它为回文串。考虑一下最暴力的算法，我们可以枚举字符串的每个子串，判断其是否为回文串，时间复杂度是O(n^{3)。当然，我们可以加点优化，枚举每个中心点，然后向两边匹配，时间复杂度是O(n}2)。不过这个复杂度依然不让人满意，因此，我们引入Manacher算法， 将时间复杂度降到线性，提高了算法效率。

二.算法流程

由于回文串分为奇回文和偶回文，因此给算法带来不小的麻烦，所以我们可以在字符串中间加入一些字符，使得其一定为奇回文，如 s= 'abaoyyo'，转换后就成了 s_new= '#&a&b&a&o&y&y&o&^'（前后加字符只是为了防止越界，后面会讲），这样，原有的回文串 'ababa' 和 'oyyo' 便变成了 '&a&b&a&' 和 '&o&y&y&o&' ，都是奇回文了。同时，我们要引入一个数组 p，p[i] 代表以 i 为中心的回文串的最大半径，如：

i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
s_new	#	&	a	&	b	&	a	&	o	&	y	&	y	&	o	&	^
p	0	1	2	1	4	1	2	1	2	1	2	5	2	1	2	1	0

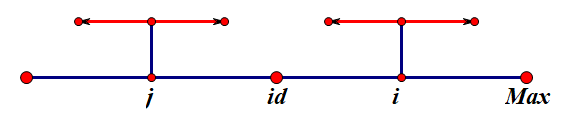
为什么开始和最后面是0呢，是因为我们在计算的时候一般不考虑这两个边界，只是防止越界用的。并且我们可以看到，p[i]-1 对应的就是在原串中以 s[i] 为中心的回文串的长度（不包括添加的字符）。那么，为什么Manacher算法要比一般的算法要快呢？因为它在求 p 的时候有一个捷径，如下图：



p[i] 是按顺序求的，我们记录 Max 为以 s_new[id] 为中心，右端点最大的值，即为 p[i]+i，其中，i，j 关于 id 对称，红色箭头代表对于一个点的扩张半径。如果 i < Max 的话，我们则有

if (i<Max)
	p[i]=min(p[id*2-i],Max-i);

三.解释

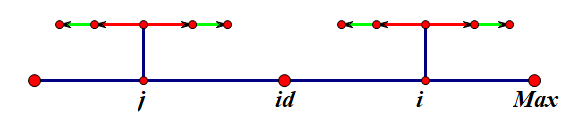
就上图而言，p[i]=p[j] 这点是毋庸置疑的，也就是 p[i]=p[id*2-i]（因为i，j 关于 id 对称）。那么，为什么要取min呢？这是我们要保证 p[i] 在直接更新的时候，右端点不能超过 Max 。那么为什么不能超过 Max 呢？我们画个图理解下



假定 p[j] 的左边界超过 id 的左边界，那么当我们直接令 p[i]=p[j] 时，i 的右边界就会超过 id 的右边界，那么这种情况是否存在呢，答案是否定的。

因为根据假设可得 j 的红色扩张部分和 i 的红色扩张部分是一样的，并且由于对称，绿色的箭头也也是对称的，既然如此，那么id的边界为什么不到两个绿色箭头的端点呢？

因此，在这种情况下，p[i] 不能直接等于 p[j]，p[i] 最大只能到 Max 的右边界，即 p[i]=Max-i 。同时，我们可以知道，在这种情况下，p[i] 是不能再扩张的。

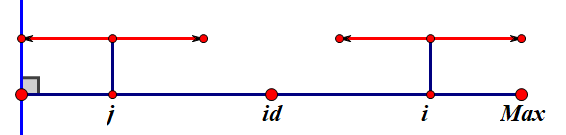
Manacher还有其他的一些情况，如下图



如果 p[j] 的左右边界都在 id 内部，那么在 p[i]=p[j] 后，p[i] 还能继续扩张吗？答案依然是否定的。

若 i 能扩张，则必定有一段扩张在 id 内部，即绿色部分。那么根据对称可知，j 也会有两段对称的绿色，那么 p[j] 为什么不扩张呢？

因此，这种情况下，p[i] 也是不能扩张的。

那么，是不是 p[i]=min(p[id*2-i],Max-i) 就好了呢？答案依然是否定的



如果说j的左边界与 id 的左边界重合，那么i的右边界就和 Max 重合。在这个情况下，i 是可以继续扩张的，之后的扩张，就只能不断的暴力匹配了

四.补充

我们开始讲到的所有情况都是建立在 i < Max 的基础之上的。那么，如果 i > Max 的话该如何呢？其实，当 i > Max 的时候，我们没有办法对 i 做出任何的假设，只能令其等于1，然后暴力匹配即可

对于 id 和 Max 而言，每次更新完 i 后进行比较，取最大值即可

暴力匹配的时候很有可能导致数组越界，因此我们在最前面和最后面加上两个不同的字符来保证其失配

五.算法复杂度

由于本算法对于匹配过的字符串基本不匹配，没有匹配过的字符串也只是O(n)扫过，因此时间复杂度可以看为是线性的，十分优秀

六.代码

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
	int x=0,f=1;char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')    f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x>=10)     print(x/10);
	putchar(x%10+'0');
}
const int N=1e6;
char s[N*2+10],t[N+10];
int p[N*2+10];
int main(){
	printf("请输入字符串\n");
	scanf("%s",t+1);
	int len=strlen(t+1),Max=0,ID=0,Ans=0,cnt=0;
	for (int i=1;i<=len;i++)	s[i<<1]=t[i],s[i<<1|1]='&';  //添加字符，使其变为奇串
	len=len<<1|1;
	s[1]='&',s[0]='%',s[len+1]='#';  //防止越界
	for (int i=1;i<=len;i++){
		p[i]=Max>i?min(p[ID*2-i],Max-i):1;  //核心部分
		while (s[i+p[i]]==s[i-p[i]])	p[i]++;  //暴力匹配
		if (Max<i+p[i])	Max=p[ID=i]+i;  //更新Max
		if (Ans<p[i])	Ans=p[i],cnt=i-p[i];  //更新答案
	}
	cnt>>=1;
	printf("最长回文串为\n");
	for (int i=cnt+1;i<cnt+Ans;i++)	putchar(t[i]);
	putchar('\n');
	return 0;
}