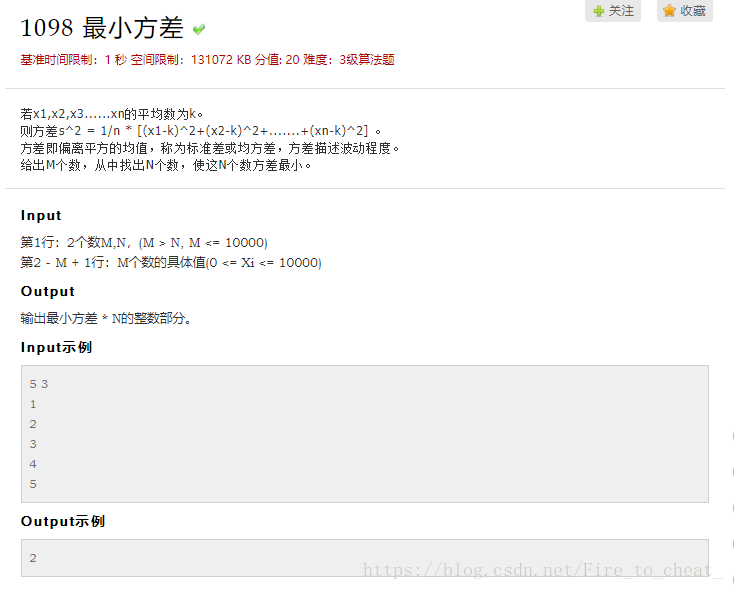
51nod 1098 最小方差

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 1e4+5;
const LL INF = 1e15+5;
LL a[MAXN], sum[MAXN], ans[MAXN];
int main()
{
    int n, m;
    while(cin>>n>>m)
    {
        for(int i=1; i<=n; i++)
            scanf("%lld",&a[i]);
        sort(a+1, a+1+n);
        sum[0] = ans[0] = 0;
        for(int i=1; i<=n; i++)
        {
            sum[i] = sum[i-1] + a[i];
            ans[i] = ans[i-1] + a[i]*a[i];
        }
        double Min = (double)INF;
        for(int i=m; i<=n; i++)
        {
            double tmp = (ans[i]-ans[i-m])-1.0*(sum[i]-sum[i-m])*(sum[i]-sum[i-m])/m;
            if(tmp < Min)
                Min = tmp;
        }
        printf("%lld\n",(LL)Min);
    }
    return 0;
}