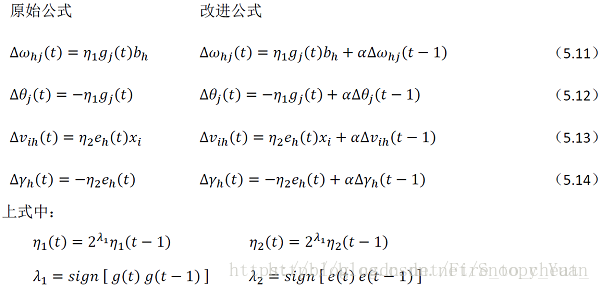BP神经网络算法改进
试设计一个算法,能通过动态调整学习率显著提升收敛速度,编程实现该算法,并选择两个UCI数据集与标准的BP算法进行实验比较。
1.方法设计
传统的BP算法改进主要有两类:
- 启发式算法:如附加动量法,自适应算法
- 数值优化法:如共轭梯度法、牛顿迭代法、Levenberg-Marquardt算法
(1)附加动量项
这是一种广泛用于加速梯度下降法收敛的优化方法。其核心思想是:在梯度下降搜索时,若当前梯度下降与前一个梯度下降的方向相同,则加速搜索,反之则降速搜索。
标准BP算法的参数更新项为:
Δω(t)=ηg(t)" role="presentation" style="position: relative;">Δω(t)=ηg(t)Δω(t)=ηg(t)
式中Δω(t)是第t次迭代的参数调整量,η为学习率,g(t)为第t次迭代计算出的梯度。" role="presentation" style="position: relative;">式中Δω(t)是第t次迭代的参数调整量,η为学习率,g(t)为第t次迭代计算出的梯度。式中Δω(t)是第t次迭代的参数调整量,η为学习率,g(t)为第t次迭代计算出的梯度。
在添加动量项后,基于梯度下降的参数更新项为:
Δω(t)=η[(1−μ)g(t)+μg(t−1)]" role="presentation" style="position: relative;">Δω(t)=η[(1−μ)g(t)+μg(t−1)]Δω(t)=η[(1−μ)g(t)+μg(t−1)]
始终,μ" role="presentation" style="position: relative;">μμ为动量因子(取值 0~1)。上式也等价于:
Δω(t)=αΔω(t−1)+ηg(t)" role="presentation" style="position: relative;">Δω(t)=αΔω(t−1)+ηg(t)Δω(t)=αΔω(t−1)+ηg(t)
式中α" role="presentation" style="position: relative;">αα 称为遗忘因子,αΔω(t−1)" role="presentation" style="position: relative;">αΔω(t−1)αΔω(t−1)表示上一次梯度下降的方向和大小信息对当前梯度下降的调整影响。
(2) 自适应学习率
附加动量法面临选取率的选取困难,进而产生收敛速度和收敛性的矛盾。于是另考虑引入学习速率自适应设计,这里给出一个·自适应设计方案:
η(t)=ση(t−1)" role="presentation" style="position: relative;">η(t)=ση(t−1)η(t)=ση(t−1)
上式中,η(t)" role="presentation" style="position: relative;">η(t)η(t)为第t次迭代时的自适应学习速率因子,下面是一种计算实力:
σ(t)=2λ" role="presentation" style="position: relative;">σ(t)=2λσ(t)=2λ
其中λ" role="presentation" style="position: relative;">λλ为梯度方向:λ=sign(g(t)(t−1))" role="presentation" style="position: relative;">λ=sign(g(t)(t−1))λ=sign(g(t)(t−1))
这样,学习率的变化可以反映前面附加动量项中的“核心思想”。
(3)算法总结
将上述两种方法结合起来,形成动态自适应学习率的BP改进算法:

从上图及书中内容可知,输出层与隐层的梯度项不同,故而对应不同的学习率 η_1 和 η_2,算法的修改主要是第7行关于参数更新的内容:
将附加动量项与学习率自适应计算代入,得出公式(5.11-5.14)的调整如下图所示:
2.对比实验
BP神经网络算法改进的更多相关文章
- bp神经网络算法
对于BP神经网络算法,由于之前一直没有应用到项目中,今日偶然之时 进行了学习, 这个算法的基本思路是这样的:不断地迭代优化网络权值,使得输入与输出之间的映射关系与所期望的映射关系一致,利用梯度下降的方 ...
- 二、单层感知器和BP神经网络算法
一.单层感知器 1958年[仅仅60年前]美国心理学家FrankRosenblant剔除一种具有单层计算单元的神经网络,称为Perceptron,即感知器.感知器研究中首次提出了自组织.自学习的思想, ...
- BP神经网络算法预测销量高低
理论以前写过:https://www.cnblogs.com/fangxiaoqi/p/11306545.html,这里根据天气.是否周末.有无促销的情况,来预测销量情况. function [ ma ...
- 数据挖掘系列(9)——BP神经网络算法与实践
神经网络曾经很火,有过一段低迷期,现在因为深度学习的原因继续火起来了.神经网络有很多种:前向传输网络.反向传输网络.递归神经网络.卷积神经网络等.本文介绍基本的反向传输神经网络(Backpropaga ...
- BP神经网络算法学习
BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是眼下应用最广泛的神经网络模型之中的一个 ...
- BP神经网络算法推导及代码实现笔记zz
一. 前言: 作为AI入门小白,参考了一些文章,想记点笔记加深印象,发出来是给有需求的童鞋学习共勉,大神轻拍! [毒鸡汤]:算法这东西,读完之后的状态多半是 --> “我是谁,我在哪?” 没事的 ...
- R_Studio(神经网络)BP神经网络算法预测销量的高低
BP神经网络 百度百科:传送门 BP(back propagation)神经网络:一种按照误差逆向传播算法训练的多层前馈神经网络,是目前应用最广泛的神经网络 #设置文件工作区间 setwd('D:\\ ...
- JAVA实现BP神经网络算法
工作中需要预测一个过程的时间,就想到了使用BP神经网络来进行预测. 简介 BP神经网络(Back Propagation Neural Network)是一种基于BP算法的人工神经网络,其使用BP算法 ...
- BP神经网络算法推导
目录 前置知识 梯度下降法 激活函数 多元复合函数求偏导的相关知识 正向计算 符号定义 输入层 隐含层 输出层 误差函数 反向传播 输出层与隐含层之间的权值调整 隐含层与输入层之间权值的调整 计算步骤 ...
随机推荐
- weblogic负载分发
博客分类: weblogic 负载均衡的实现方式有很多种,这里只介绍三种相对来说成本较低的方案(维护成本以及费用成本)weblogic自带的proxy.apache.nginx 1.weblogic自 ...
- 2>MSVCRTD.lib(MSVCR100D.dll) : error LNK2005: _calloc 已经在 LIBCMTD.lib(dbgcalloc.obj) 中定义
使用VS2010,在FireBreath里面调用ortp库和Speex库.编译的时候出现错误: 2>MSVCRTD.lib(MSVCR100D.dll) : error LNK2005: _ca ...
- 嵌入式开发之davinci--- 8148/8168/8127 中的添加算饭scd 场景检测 文档简介
Osd Scd (1) Introduction over view a) scene change detection block diagram a) gr ...
- 【iOS系列】-xib封装使用
[iOS系列]-xib封装使用 Xib文件可以用来描述某一块局部的UI界面 Xib文件的加载 修改xib文件的大小size(Freeform) 第一: NSArray *objs = [[NSBund ...
- 【iOS系列】-UIButton的非常规使用
[iOS系列]-UIButton的非常规使用 主要介绍UIButton在开发中得小技巧,使用好了,可以达到很奇妙的效果. 1:设置按钮内边距属性,可以呈现出相框的效果 btn.contentEdgeI ...
- Django框架之路由
1,路由系统就是url系统,整个url系统就是请求进入Django项目的入口,每一个请求的种类由url分析完毕并再去返回相应的响应,它的本质是url与要为该url调用的视图函数之间的映射关系表(当项目 ...
- commons-fileupload、smartUpload和commons-net-ftp
1.本地上传 在许多Web站点应用中都需要为用户提供通过浏览器上传文档资料的功能,例如,上传个人相片.共享资料等.在DRP中,就有这个一个功能,需要将对应的物料图片上传并显示.对于上传功能,其实在浏览 ...
- YTU 2928: 取不重复的子串。
2928: 取不重复的子串. 时间限制: 1 Sec 内存限制: 128 MB 提交: 5 解决: 5 题目描述 输入字母构成的字符串(不大于30字符)从中读取3个不重复的字符,求所有取法,取出的 ...
- JFreeChart教程(二)(转)
JFreeChart教程(二) 分类: java Component2007-05-31 17:01 8408人阅读 评论(11) 收藏 举报 jfreechartstringplotclassdat ...
- idea项目文件名为红色的解决办法
设置项目的版本控制为none或者对应的版本控制,如下图,添加对应项目的版本控制为none: