HTML5中手势原理分析与数学知识的实践

摘要：在这触控屏的时代，人性化的手势操作已经深入了我们生活的每个部分。现代应用越来越重视与用户的交互及体验，手势是最直接且最为有效的交互方式，一个好的手势交互，能降低用户的使用成本和流程，大大提高了用户的体验。

本文主要是解析了移动端常用手势的原理，及从前端的角度学习过程中所使用的数学知识。希望能对大家有一点点的启发作用。

---

一、引言

在这触控屏的时代，人性化的手势操作已经深入了我们生活的每个部分。现代应用越来越重视与用户的交互及体验，手势是最直接且最为有效的交互方式，一个好的手势交互，能降低用户的使用成本和流程，大大提高了用户的体验。

近期，公司的多个项目中都对手势有着较高的需求，已有的手势库无法完全cover，因此便撸了一个轻量、便于使用的移动端手势库。这篇博文主要是解析了移动端常用手势的原理，及从前端的角度学习过程中所使用的数学知识。希望能对大家有一点点的启发作用，也期待大神们指出不足甚至错误，感恩。

主要讲解项目中经常使用到的五种手势：

拖动: drag

双指缩放: pinch

双指旋转: rotate

单指缩放: singlePinch

单指旋转: singleRotate

Tips :因为 tap 及 swipe 很多基础库中包含，为了轻便，因此并没有包含,但如果需要，可进行扩展;

二、实现原理

众所周知，所有的手势都是基于浏览器原生事件touchstart, touchmove, touchend, touchcancel进行的上层封装，因此封装的思路是通过一个个相互独立的事件回调仓库handleBus，然后在原生touch事件中符合条件的时机触发并传出计算后的参数值，完成手势的操作。实现原理较为简单清晰，先不急，我们先来理清一些使用到的数学概念并结合代码，将数学运用到实际问题中，数学部分可能会比较枯燥，但希望大家坚持读完，相信会收益良多。

二、基础数学知识函数

我们常见的坐标系属于线性空间，或称向量空间(Vector Space)。这个空间是一个由点(Point) 和 向量(Vector) 所组成集合。

2.1 点(Point)

可以理解为我们的坐标点,例如原点O(0,0),A(-1,2)，通过原生事件对象的touches可以获取触摸点的坐标，参数index代表第几接触点；

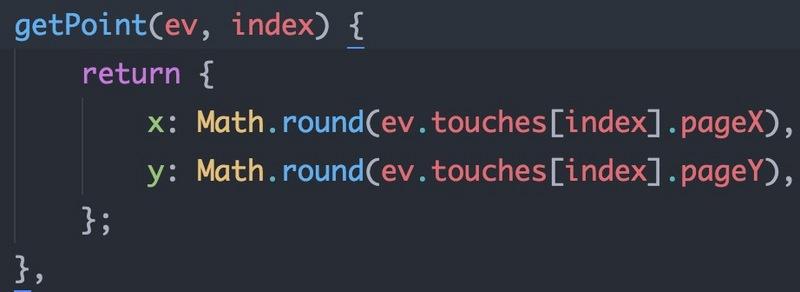
2.2 向量(Vector）

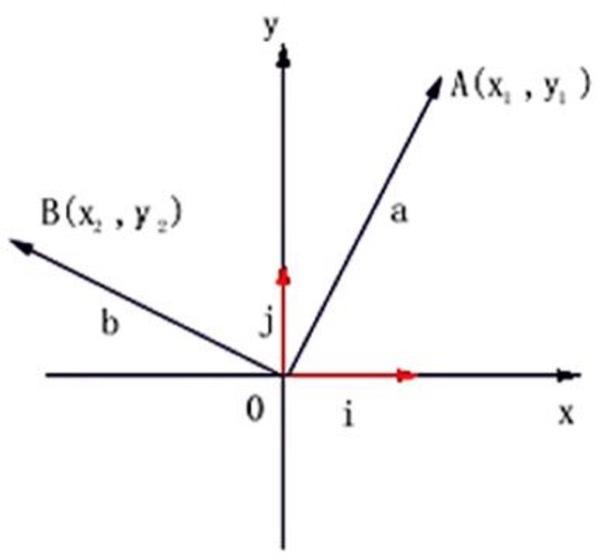
是坐标系中一种 既有大小也有方向的线段，例如由原点O(0,0)指向点A(1,1)的箭头线段，称为向量a，则a=(1-0,1-0)=(1,1);

如下图所示，其中i与j向量称为该坐标系的单位向量，也称为基向量，我们常见的坐标系单位为1,即i=(1,0)；j=(0,1)；

获取向量的函数：

2.3 向量模

代表 向量的长度，记为|a|，是一个标量，只有大小，没有方向;

几何意义代表的是以x,y为直角边的直角三角形的斜边，通过勾股定理进行计算；

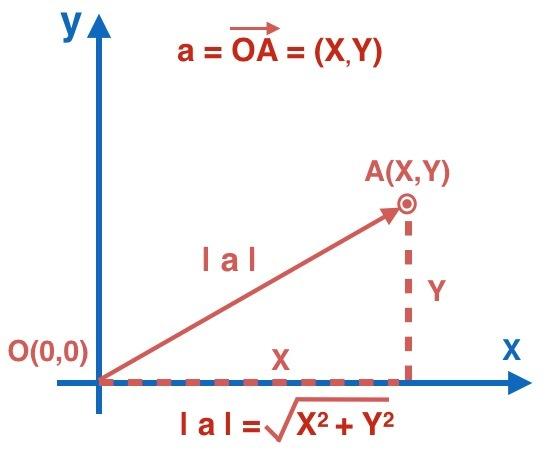
getLength函数：

2.4 向量的数量积

向量同样也具有可以运算的属性，它可以进行加、减、乘、数量积和向量积等运算，接下来就介绍下我们使用到的数量积这个概念，也称为点积，被定义为公式：

当a=(x1,y1),b=(x2,y2)，则a·b=|a|·|b|·cosθ=x1·x2+y1·y2；

2.5 共线定理

共线，即两个向量处于 平行 的状态，当a=(x1,y1),b=(x2,y2)，则存在唯一的一个实数λ，使得a=λb，代入坐标点后，可以得到 x1·y2= y1·x2;

因此当x1·y2-x2·y1>0 时，既斜率 ka > kb ，所以此时b向量相对于a向量是属于顺时针旋转，反之，则为逆时针；

2.6 旋转角度

通过数量积公式我们可以推到求出两个向量的夹角：

cosθ=(x1·x2+y1·y2)/(|a|·|b|);

然后通过共线定理我们可以判断出旋转的方向，函数定义为：

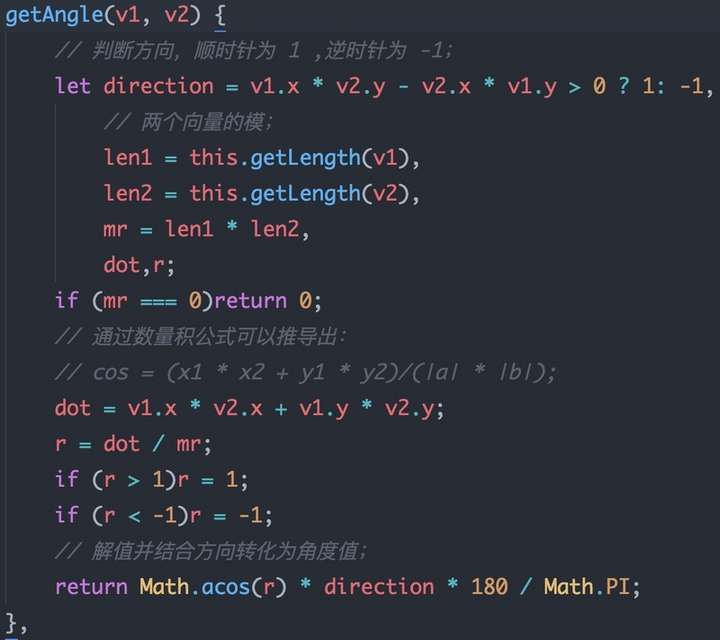
2.7 矩阵与变换

由于空间最本质的特征就是其可以容纳运动，因此在线性空间中，我们用向量来刻画对象，而矩阵便是用来描述对象的运动；而矩阵是如何描述运动的呢?

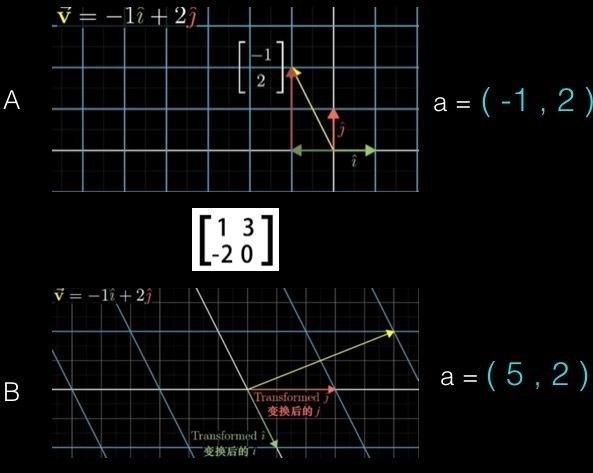
我们知道，通过一个坐标系基向量便可以确定一个向量，例如 a=(-1,2),我们通常约定的基向量是 i = (1,0) 与 j = (0,1)； 因此:

a = -1i + 2j = -1(1,0) + 2(0,1) = (-1+0,0+2) = (-1,2);

而矩阵变换的，其实便是通过矩阵转换了基向量，从而完成了向量的变换；

例如上面的栗子，把a向量通过矩阵(1,2,3,0)进行变换，此时基向量i由 (1,0)变换成(1,-2)与j由(0,1)变换成(3,0),沿用上面的推导，则

a = -1i + 2j = -1(-1,2) + 2(3,0) = (5,-2);

如下图所示：
A图表示变换之前的坐标系，此时a=(-1,2)，通过矩阵变换后，基向量i，j的变换引起了坐标系的变换，变成了下图B，因此a向量由(-1,2)变换成了(5,-2)；其实向量与坐标系的关联不变(a = -1i+2j)，是基向量引起坐标系变化，然后坐标系沿用关联导致了向量的变化；

2.7.1 结合代码

其实CSS的transform等变换便是通过矩阵进行的，我们平时所写的translate/rotate等语法类似于一种封装好的语法糖，便于快捷使用，而在底层都会被转换成矩阵的形式。例如transform:translate(-30px,-30px)编译后会被转换成transform : matrix(1,0,0,1,30,30);

通常在二维坐标系中，只需要 2X2 的矩阵便足以描述所有的变换了， 但由于CSS是处于3D环境中的，因此CSS中使用的是 3X3 的矩阵，表示为：

其中第三行的0,0,1代表的就是z轴的默认参数。这个矩阵中，(a,b) 即为坐标轴的 i基，而(c,d)既为j基,e为x轴的偏移量,f为y轴的偏移量;因此上栗便很好理解，translate并没有导致i，j基改变，只是发生了偏移，因此translate(-30px,-30px) ==> matrix(1,0,0,1,30,30)~

所有的transform语句，都会发生对应的转换，如下：

// 发生偏移，但基向量不变；

transform:translate(x,y) ==> transform:matrix(1,0,0,1,x,y)

// 基向量旋转；

transform:rotate(θdeg)==> transform:matrix(cos(θ·π/180),sin(θ·π/180),-sin(θ·π/180),cos(θ·π/180),0,0)

// 基向量放大且方向不变；

transform:scale(s) ==> transform:matrix(s,0,0,s,0,0)

translate/rotate/scale等语法十分强大，让我们的代码更为可读且方便书写，但是matrix有着更强大的转换特性，通过matrix，可以发生任何方式的变换，例如我们常见的镜像对称，transform:matrix(-1,0,0,1,0,0);

2.7.2 MatrixTo

然而matrix虽然强大，但可读性却不好，而且我们的写入是通过translate/rotate/scale的属性,然而通过getComputedStyle读取到的 transform却是matrix:

transform:matrix(1.41421, 1.41421, -1.41421, 1.41421, -50, -50);

请问这个元素发生了怎么样的变化?。。这就一脸懵逼了。-_-|||

因此，我们必须要有个方法，来将matrix翻译成我们更为熟悉的translate/rotate/scale方式，在理解了其原理后，我们便可以着手开始表演咯~

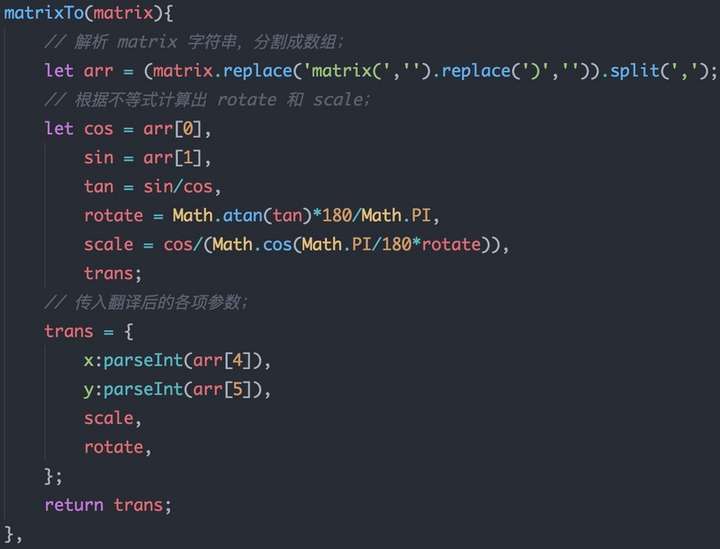
我们知道，前4个参数会同时受到rotate和scale的影响，具有两个变量，因此需要通过前两个参数根据上面的转换方式列出两个不等式：

cos(θ·π/180)*s=1.41421;
sin(θ·π/180)*s=1.41421;

将两个不等式相除，即可以轻松求出θ和s了，perfect！！函数如下：

三、手势原理

接下来我们将上面的函数用到实际环境中，通过图示的方式来模拟手势的操作，简要地讲解手势计算的原理。希望各位大神理解这些基础的原理后，能创造出更多炫酷的手势，像我们在mac触控板上使用的一样。

下面图例：

圆点: 代表手指的触碰点;
两个圆点之间的虚线段: 代表双指操作时组成的向量;
a向量/A点：代表在 touchstart 时获取的初始向量/初始点；
b向量/B点：代表在 touchmove 时获取的实时向量/实时点；
坐标轴底部的公式代表需要计算的值；

3.1 Drag(拖动事件)

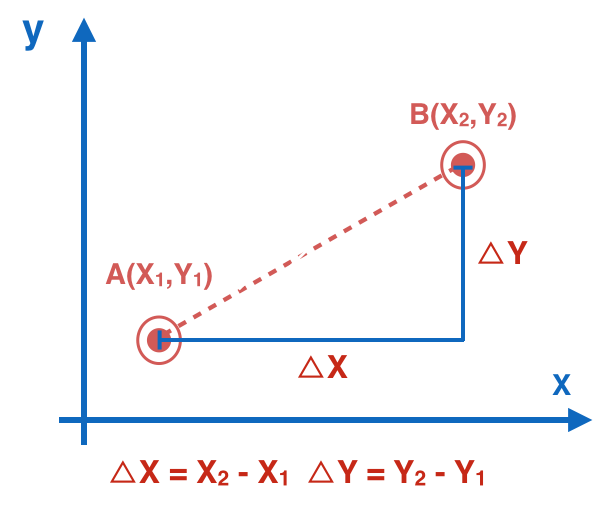
上图是模拟了拖动手势，由A点移动到B点，我们要计算的便是这个过程的偏移量；

因此我们在touchstart中记录初始点A的坐标：

// 获取初始点A；
let startPoint = getPoint(ev,0);

然后在touchmove事件中获取当前点并实时的计算出△x与△y：

// 实时获取初始点B；
let curPoint = getPoint(ev,0);

// 通过A、B两点，实时的计算出位移增量，触发 drag 事件并传出参数；
_eventFire('drag', {
    delta: {
        deltaX: curPoint.x - startPoint.x,
        deltaY: curPoint.y - startPoint.y,
    },
    origin: ev,
});

Tips: fire函数即遍历执行drag事件对应的回调仓库即可；

3.2 Pinch(双指缩放)

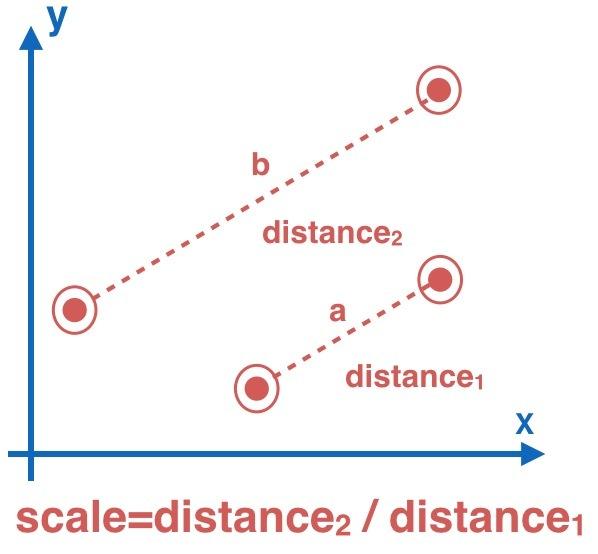
上图是双指缩放的模拟图，双指由a向量放大到b向量，通过初始状态时的a向量的模与touchmove中获取的b向量的模进行计算，便可得出缩放值：

// touchstart中计算初始双指的向量模；
let vector1 = getVector(secondPoint, startPoint);
let pinchStartLength = getLength(vector1);

// touchmove中计算实时的双指向量模；
let vector2 = getVector(curSecPoint, curPoint);
let pinchLength = getLength(vector2);
this._eventFire('pinch', {
    delta: {
        scale: pinchLength / pinchStartLength,
    },
    origin: ev,
});

3.3 Rotate(双指旋转)

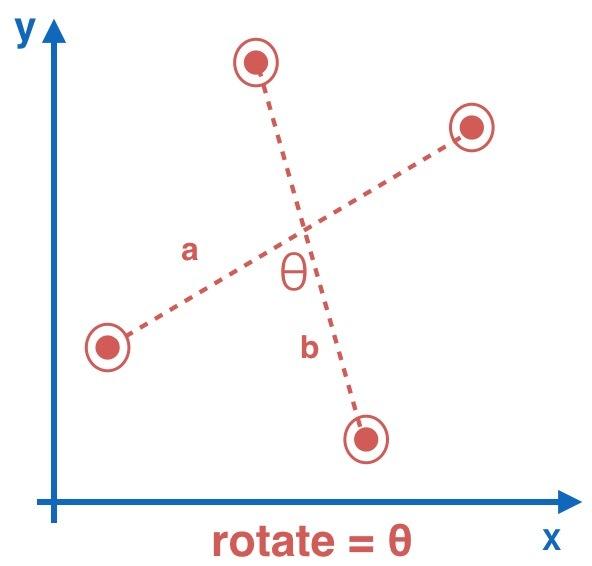
初始时双指向量a，旋转到b向量，θ便是我们需要的值，因此只要通过我们上面构建的getAngle函数，便可求出旋转的角度：

// a向量；
let vector1 = getVector(secondPoint, startPoint);

// b向量；
let vector2 = getVector(curSecPoint, curPoint);

// 触发事件;
this._eventFire('rotate', {
    delta: {
        rotate: getAngle(vector1, vector2),
    },
    origin: ev,
});

3.4 singlePinch(单指缩放)

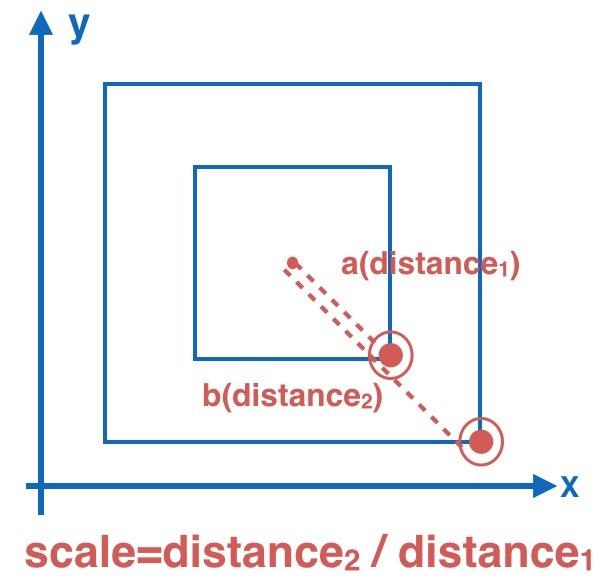
与上面的手势不同，单指缩放和单指旋转都需要多个特有概念：

操作元素(operator)：需要操作的元素。上面三个手势其实并不关心操作元素，因为单纯靠手势自身，便能计算得出正确的参数值，而单指缩放和旋转需要依赖于操作元素的基准点(操作元素的中心点)进行计算；

按钮：因为单指的手势与拖动(drag)手势是相互冲突的，需要一种特殊的交互方式来进行区分，这里是通过特定的区域来区分，类似于一个按钮，当在按钮上操作时，是单指缩放或者旋转，而在按钮区域外，则是常规的拖动，实践证明，这是一个用户很容易接受且体验较好的操作方式；

图中由a向量单指放大到b向量，对操作元(正方形)素进行了中心放大，此时缩放值即为b向量的模 / a向量的模；

// 计算单指操作时的基准点，获取operator的中心点；
let singleBasePoint = getBasePoint(operator);

// touchstart 中计算初始向量模；
let pinchV1 = getVector(startPoint,singleBasePoint);
singlePinchStartLength = getLength(pinchV1);

// touchmove 中计算实时向量模；
pinchV2 = getVector(curPoint, singleBasePoint);
singlePinchLength = getLength(pinchV2);

// 触发事件；
this._eventFire('singlePinch', {
    delta: {
        scale: singlePinchLength / singlePinchStartLength,
    },
    origin: ev,
});

3.5 singleRotate(单指旋转)

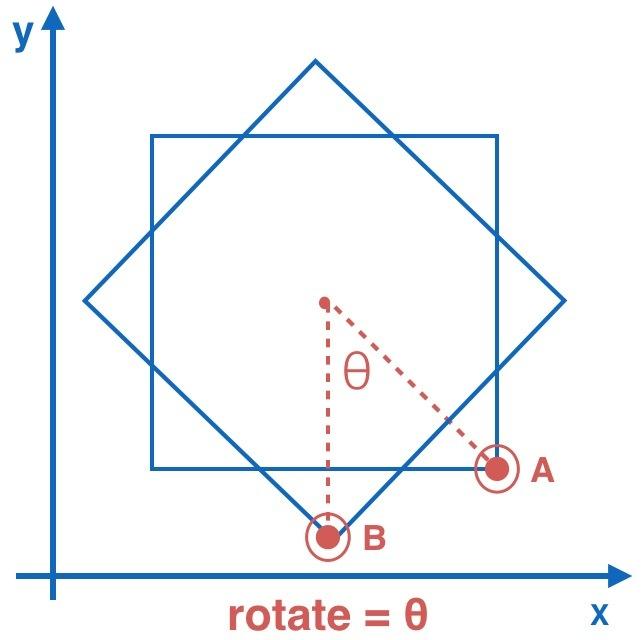
结合单指缩放和双指旋转，可以很简单的知道 θ便是我们需要的旋转角度；

// 获取初始向量与实时向量
let rotateV1 = getVector(startPoint, singleBasePoint);
let rotateV2 = getVector(curPoint, singleBasePoint);

// 通过 getAngle 获取旋转角度并触发事件；
this._eventFire('singleRotate', {
    delta: {
        rotate: getAngle(rotateV1, rotateV2),
    },
    origin: ev,
});

3.6 运动增量

由于touchmove事件是个高频率的实时触发事件，一个拖动操作，其实触发了N次的touchmove事件，因此计算出来的值只是一种增量，即代表的是一次 touchmove事件增加的值，只代表一段很小的值，并不是最终的结果值，因此需要由mtouch.js外部维护一个位置数据，类似于:

//    真实位置数据；
let dragTrans = {x = 0,y = 0};

// 累加上 mtouch 所传递出的增量 deltaX 与 deltaY;
dragTrans.x += ev.delta.deltaX;
dragTrans.y += ev.delta.deltaY;

// 通过 transform 直接操作元素；
set($drag,dragTrans);

3.7 初始位置

维护外部的这个位置数据，如果初始值像上述那样直接取0，则遇到使用css设置了transform属性的元素便无法正确识别了，会导致操作元素开始时瞬间跳回(0,0)的点，因此我们需要初始去获取一个元素真实的位置值，再进行维护与操作。此时，便需要用到上面我们提到的getComputedStyle方法与matrixTo函数：

// 获取css transform属性，此时得到的是一个矩阵数据；
// transform:matrix(1.41421,1.41421,-1.41421,1.41421,-50,-50);
let style = window.getComputedStyle(el,null);
let cssTrans = style.transform || style.webkitTransform;

// 按规则进行转换，得到：
let initTrans = _.matrixTo(cssTrans);

// {x:-50,y:-50,scale:2,rotate:45};
// 即该元素设置了：transform:translate(-50px,-50px) scale(2) rotate(45deg);

转载：https://zhuanlan.zhihu.com/p/36696618